北师大版八年级下册2.2 不等式的基本性质 课件(共31张PPT)
文档属性
| 名称 | 北师大版八年级下册2.2 不等式的基本性质 课件(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 309.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-17 00:00:00 | ||
图片预览











文档简介
第二章 一元一次不等式与一元一次不等式组
2.2 不等式的基本性质
一、不等式的基本性质1
二、不等式的基本性质2
三、不等式的基本性质3
学习目标
如果a=b,那么
情景引入
等式基本性质1:在等式的两边都加上(或减去)
同一个数或整式,所得的结果仍是等式。
等式基本性质2:在等式的两边都乘以或除以同
一个数(除数不为0),所得的结果仍是等式。
Ⅰ、对于4<6,那么
新知探究
对比“等式基本性质1”,你有什么想法?
新知归纳
不等式的基本性质:
(1)不等式的两边都加上(或减去)同一个整式,不
等号的方向不变;
性质1:不等式两边都加(或减)同一个整式,不等号
的方向不变,即如果a>b,那么a±c>b±c.
根据不等式的基本性质1,两边都加5,得
x > -1+5,
即 x>4;
解:
将下列不等式化成“x>a”或“x<a”的形式:
x-5>-1;
例1
1.已知a<b,用“>”或“<”填空:
(1)a+2________b+2;
(2)a-3________b-3;
(3)a+c________b+c;
(4)a-b________0.
<
<
<
<
牛刀小试
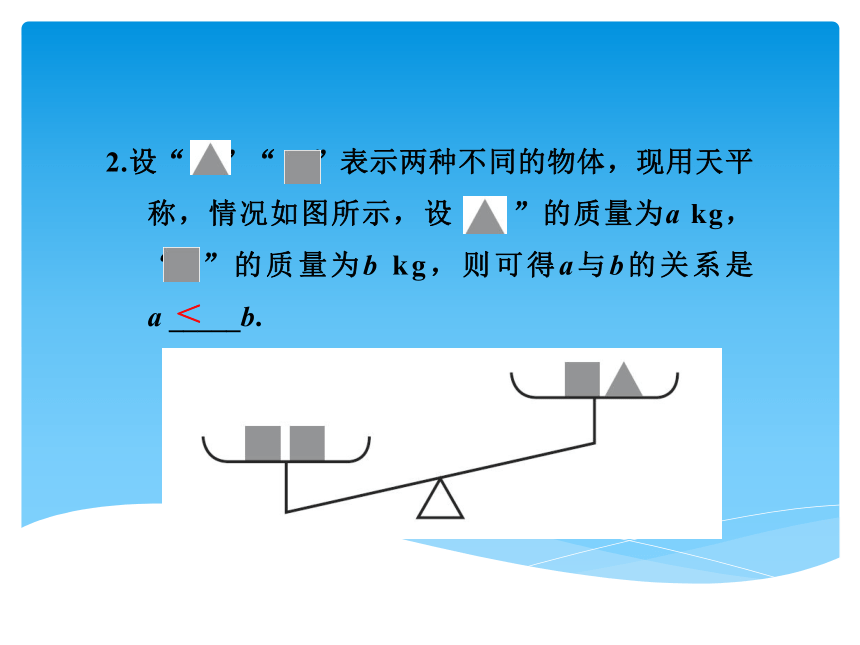
2.设“ ”“ ”表示两种不同的物体,现用天平
称,情况如图所示,设“ ”的质量为a kg,
“ ”的质量为b kg,则可得a与b的关系是
a _____b.
<
3.估计 +1的值( )
A.在1和2之间
B.在2和3之间
C.在3和4之间
D.在4和5之间
C
4.若a< -1<b,且a,b是两
个连续整数,则a+b的值是( )
A.1 B.2
C.3 D.4
C
Ⅱ、对于4<6,那么
新知探究
对比“等式基本性质2”,你有什么想法?
新知归纳
不等式的基本性质:
(1)不等式的两边都加上(或减去)同一个整式,不等号的方向不变;
(2)不等式的两边都乘以(或除以)同一个正数,不等号的方向不变;
性质2:不等式两边都乘(或除以)同一个正数,不等
号的方向不变,即如果a>b,c>0,那么ac>bc
(或 ).
∵c为实数,∴c2≥0.
当c2=0时,在a>b两边都乘c2时,有ac2=bc2;
当c2>0时,在a>b两边都乘c2时,有ac2>bc2.
综上所述,得ac2≥bc2.
例2
导引:
若a>b,c为实数,则ac2______bc2.
≥
c2的值应该大于或等于0,如果忽略了等于0这一
特殊情况,会导致不等式变形错误,即当乘的一个
数是字母常数时,在判别它的正、负性时,还要考
虑它是否有为0的情况.
总 结
1.由3a<4b,两边_____________________,可变形
为 .
2.若m>n,则下列不等式不一定成立的是( )
A.m+2>n+2 B.2m>2n
C. D.m2<n2
同乘 (或同除以12)
D
利剑出鞘
Ⅲ、对于4<6,那么
新知探究
对比“等式基本性质2”,你有什么想法?
新知归纳
不等式的基本性质:
(1)不等式的两边都加上(或减去)同一个整式,不
等号的方向不变;
(2)不等式的两边都乘以(或除以)同一个正数,不
等号的方向不变;
(3)不等式的两边都乘以(或除以)同一个负数,不
等号的方向改变。
根据不等式的基本性质3,两边都除以-2,得
x < .
解:
将下列不等式化成“x>a”或“x<a”的形式:
-2x>3.
例3
∵m<6,∴m-6<0,即m-6为负数.
导引:
已知m<6,解关于x的不等式(m-6)x<m-6.
例4
∵m<6,
∴m-6<0,即m-6为负数.
∴将(m-6)x<m-6两边同除以(m-6),得x>1.
解:
不等式两边都除以同一个负数时,不等号的方向
必须改变,否则会造成错误;当除以的一个数是字母
常数时,要注意先判断这个字母常数的正、负性,再
确定是利用不等式的基本性质2还是基本性质3进行解
答.
总 结
1.将下列不等式化成“x>a”或“x<a”的形式:
(1) x-1>2; (2)-x< ; (3) x<3.1
(1)x-1>2.根据不等式的基本性质1,两边都加上1,
得x-1+1>2+1,即x>3.
(2)-x< 根据不等式的基本性质3,两边都除
以-1,得x>-
(3) x≤3. 根据不等式的基本性质2,两边都乘2,
得x≤6.
解:
披荆斩棘
2.已知x>y,下列不等式一定成立吗?
(1) x-6 <y-6; (2) 3x< 3y;
(3) -2x<-2y; (4) 2x + 1 > 2y + 1.
(1)不成立;(2)不成立;(3)成立;(4)成立.
解:
3.有一道这样的题:“由★x>1得到x< ”,
则题中★表示的是( )
A.非正数 B.正数
C.非负数 D.负数
D
4.已知实数a,b满足a+1>b+1,则下列选项错误的为( )
A.a>b B.a+2>b+2
C.-a<-b D.2a>3b
D
5.实数a,b,c在数轴上对应的点如图所示,则下列式子中正确的是( )
A.a-c>b-c B.a+cC.ac>bc D.
B
6.已知m<5,将不等式(m-5)x>m-5变形为“x<a”或“x>a”的形式.
易错点1:受思维定式的影响,忽视运用不等式的基本 性质3时要改变不等号的方向
∵m<5,
∴m-5<0(不等式的基本性质1).
由(m-5)x>m-5,得
x<1(不等式的基本性质3).
解:
此题易忽视运用不等式的基本性质3时,不等号的方向改变,从而出现由(m-5)x>m-5,得到x>1的错误.
7.若a>b,c为实数,试比较ac2与bc2的大小.
易错点:运用不等式的基本性质2或基本性质3时易忽略此数(或式子)为0的情况
此题应分c>0,c=0,c<0三种情况进行讨论.
当c>0时,c2>0,由a>b得到ac2>bc2;
当c=0时,c2=0,由a>b得到ac2=bc2;
当c<0时,c2>0,由a>b得到ac2>bc2.
综上所述,当c≠0时,ac2>bc2;当c=0时,ac2=bc2.
解:
此题学生易忽略c=0的情况,从而出现由a>b得到ac2>bc2的错误.
不等式的基本性质:
不等式的基本性质1 不等式的两边都加(或减)
同一个整式,不等号的方向不变.
不等式的基本性质2 不等式两边都乘(或除以)同一
个正数,不等号的方向不变.
不等式的基本性质3 不等式两边都乘(或除以)同一
个负数,不等号的方向改变.
今天你学到了吗?
2.2 不等式的基本性质
一、不等式的基本性质1
二、不等式的基本性质2
三、不等式的基本性质3
学习目标
如果a=b,那么
情景引入
等式基本性质1:在等式的两边都加上(或减去)
同一个数或整式,所得的结果仍是等式。
等式基本性质2:在等式的两边都乘以或除以同
一个数(除数不为0),所得的结果仍是等式。
Ⅰ、对于4<6,那么
新知探究
对比“等式基本性质1”,你有什么想法?
新知归纳
不等式的基本性质:
(1)不等式的两边都加上(或减去)同一个整式,不
等号的方向不变;
性质1:不等式两边都加(或减)同一个整式,不等号
的方向不变,即如果a>b,那么a±c>b±c.
根据不等式的基本性质1,两边都加5,得
x > -1+5,
即 x>4;
解:
将下列不等式化成“x>a”或“x<a”的形式:
x-5>-1;
例1
1.已知a<b,用“>”或“<”填空:
(1)a+2________b+2;
(2)a-3________b-3;
(3)a+c________b+c;
(4)a-b________0.
<
<
<
<
牛刀小试
2.设“ ”“ ”表示两种不同的物体,现用天平
称,情况如图所示,设“ ”的质量为a kg,
“ ”的质量为b kg,则可得a与b的关系是
a _____b.
<
3.估计 +1的值( )
A.在1和2之间
B.在2和3之间
C.在3和4之间
D.在4和5之间
C
4.若a< -1<b,且a,b是两
个连续整数,则a+b的值是( )
A.1 B.2
C.3 D.4
C
Ⅱ、对于4<6,那么
新知探究
对比“等式基本性质2”,你有什么想法?
新知归纳
不等式的基本性质:
(1)不等式的两边都加上(或减去)同一个整式,不等号的方向不变;
(2)不等式的两边都乘以(或除以)同一个正数,不等号的方向不变;
性质2:不等式两边都乘(或除以)同一个正数,不等
号的方向不变,即如果a>b,c>0,那么ac>bc
(或 ).
∵c为实数,∴c2≥0.
当c2=0时,在a>b两边都乘c2时,有ac2=bc2;
当c2>0时,在a>b两边都乘c2时,有ac2>bc2.
综上所述,得ac2≥bc2.
例2
导引:
若a>b,c为实数,则ac2______bc2.
≥
c2的值应该大于或等于0,如果忽略了等于0这一
特殊情况,会导致不等式变形错误,即当乘的一个
数是字母常数时,在判别它的正、负性时,还要考
虑它是否有为0的情况.
总 结
1.由3a<4b,两边_____________________,可变形
为 .
2.若m>n,则下列不等式不一定成立的是( )
A.m+2>n+2 B.2m>2n
C. D.m2<n2
同乘 (或同除以12)
D
利剑出鞘
Ⅲ、对于4<6,那么
新知探究
对比“等式基本性质2”,你有什么想法?
新知归纳
不等式的基本性质:
(1)不等式的两边都加上(或减去)同一个整式,不
等号的方向不变;
(2)不等式的两边都乘以(或除以)同一个正数,不
等号的方向不变;
(3)不等式的两边都乘以(或除以)同一个负数,不
等号的方向改变。
根据不等式的基本性质3,两边都除以-2,得
x < .
解:
将下列不等式化成“x>a”或“x<a”的形式:
-2x>3.
例3
∵m<6,∴m-6<0,即m-6为负数.
导引:
已知m<6,解关于x的不等式(m-6)x<m-6.
例4
∵m<6,
∴m-6<0,即m-6为负数.
∴将(m-6)x<m-6两边同除以(m-6),得x>1.
解:
不等式两边都除以同一个负数时,不等号的方向
必须改变,否则会造成错误;当除以的一个数是字母
常数时,要注意先判断这个字母常数的正、负性,再
确定是利用不等式的基本性质2还是基本性质3进行解
答.
总 结
1.将下列不等式化成“x>a”或“x<a”的形式:
(1) x-1>2; (2)-x< ; (3) x<3.1
(1)x-1>2.根据不等式的基本性质1,两边都加上1,
得x-1+1>2+1,即x>3.
(2)-x< 根据不等式的基本性质3,两边都除
以-1,得x>-
(3) x≤3. 根据不等式的基本性质2,两边都乘2,
得x≤6.
解:
披荆斩棘
2.已知x>y,下列不等式一定成立吗?
(1) x-6 <y-6; (2) 3x< 3y;
(3) -2x<-2y; (4) 2x + 1 > 2y + 1.
(1)不成立;(2)不成立;(3)成立;(4)成立.
解:
3.有一道这样的题:“由★x>1得到x< ”,
则题中★表示的是( )
A.非正数 B.正数
C.非负数 D.负数
D
4.已知实数a,b满足a+1>b+1,则下列选项错误的为( )
A.a>b B.a+2>b+2
C.-a<-b D.2a>3b
D
5.实数a,b,c在数轴上对应的点如图所示,则下列式子中正确的是( )
A.a-c>b-c B.a+c
B
6.已知m<5,将不等式(m-5)x>m-5变形为“x<a”或“x>a”的形式.
易错点1:受思维定式的影响,忽视运用不等式的基本 性质3时要改变不等号的方向
∵m<5,
∴m-5<0(不等式的基本性质1).
由(m-5)x>m-5,得
x<1(不等式的基本性质3).
解:
此题易忽视运用不等式的基本性质3时,不等号的方向改变,从而出现由(m-5)x>m-5,得到x>1的错误.
7.若a>b,c为实数,试比较ac2与bc2的大小.
易错点:运用不等式的基本性质2或基本性质3时易忽略此数(或式子)为0的情况
此题应分c>0,c=0,c<0三种情况进行讨论.
当c>0时,c2>0,由a>b得到ac2>bc2;
当c=0时,c2=0,由a>b得到ac2=bc2;
当c<0时,c2>0,由a>b得到ac2>bc2.
综上所述,当c≠0时,ac2>bc2;当c=0时,ac2=bc2.
解:
此题学生易忽略c=0的情况,从而出现由a>b得到ac2>bc2的错误.
不等式的基本性质:
不等式的基本性质1 不等式的两边都加(或减)
同一个整式,不等号的方向不变.
不等式的基本性质2 不等式两边都乘(或除以)同一
个正数,不等号的方向不变.
不等式的基本性质3 不等式两边都乘(或除以)同一
个负数,不等号的方向改变.
今天你学到了吗?
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
