北师大版八年级下册数学2.3.不等式的解集 课件 (共22张PPT)
文档属性
| 名称 | 北师大版八年级下册数学2.3.不等式的解集 课件 (共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-17 00:00:00 | ||
图片预览








文档简介
2.3不等式的解集
认知目标:不等式的解集的两种表示方法.
学习目标
理解目标:求不等式的整数解.
运用目标:求不等式的解集并能在数轴上表示出来.
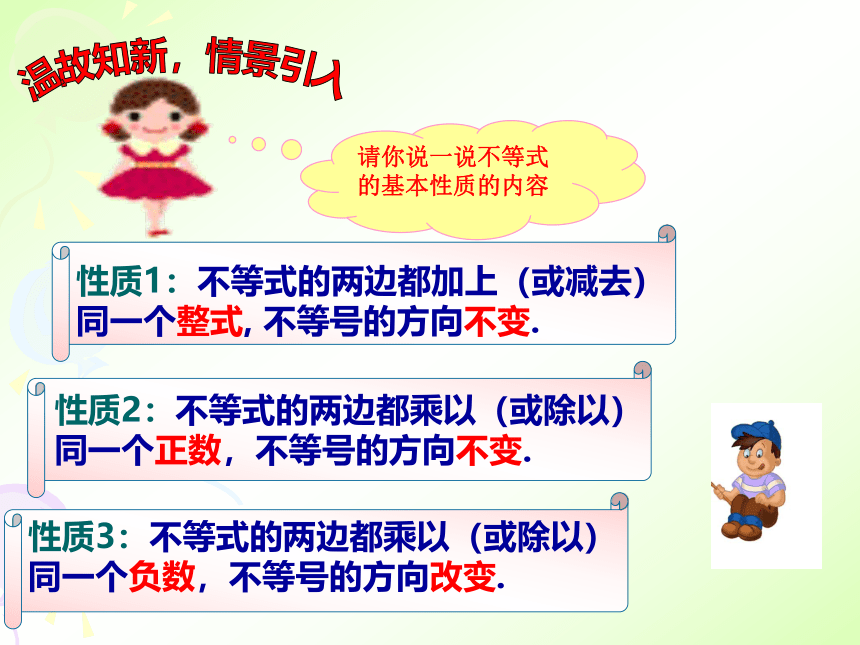
温故知新,情景引入
请你说一说不等式的基本性质的内容
性质1:不等式的两边都加上(或减去)同一个整式, 不等号的方向不变.
性质2:不等式的两边都乘以(或除以)
同一个正数,不等号的方向不变.
性质3:不等式的两边都乘以(或除以)同一个负数,不等号的方向改变.
2.方程的解的定义是什么?
使得方程中等号两边相等的未知数的值叫做方程的解;
3.类似地,你认为什么是不等式的解?
类比思考
燃放某种烟花时,为了确保安全,人在
点燃导火线后要在燃放前转移到10m以外
的安全区域。已知导火线的燃烧速度为
0.02m/s,人离开的速度为4m/s,那么导
火线的长度应满足什么条件?
观各抒己见
1、算数方法
燃放者离开时间要多于: 秒;
引火线的长度要大于: 米
设引火线的长度为 时,燃放者在燃放前刚好可以转移到 处
2、利用方程
所以:引火线的长度要大于5厘米。
合作学习
3、利用不等式
解:设引火线的长度为 时,根据题意,得
根据不等式的基本性质,得
所以,引火线的长度应大于5cm
1.x=4、5、6、8能使不等式x>5成立么?
x
2.你还能说出几个使不等式x>5成立的 值吗?你认为不等式x>5的解有几个?它们有什么特点?
3.你能说出使不等式x2≤0成立的x值吗?
探究1:不等式的解、解集的概念。
=6、8能使不等式 x >5成立
x =9、10、11……,有无数个,它们都比5大
x=0
归纳结论
不等式的解:能使不等式成立的未知数的值;
不等式的解集:
一个含有未知数的不等式的所有解;
例如, =3.5、4、5、5.5都是不等式 的解
什么叫解不等式?
可类比什么叫解方程 ?
求不等式的解集的过程,叫做解不等式。
讨论
(1) 不等式 的解有多少个?
(2)不等式的解与方程的解有什么不同?
无数个
不等式的解是一个范围,而方程的解是固定个数限制的,如:一次方程的解是一个,二次方程的解是两个等等
例1、
下列说法中,错误的是( )
A、不等式 <2的正整数解有一个
B、-2是不等式2 -1<0的一个解
C、不等式-3 >9的解集是 >-3
D、不等式 <10的整数解有无数个
C
探究2:在数轴上表示不等式的解集。
1、 是不是 的解, 呢?你能用自己的方式将 的解集表示在数轴上吗?
不等式 的解集可以用数轴上表示5的点的右边部分来表示。在数轴上表示5的点的位置上画空心圆圈,表示5不在这个解集内。
-3 -2 -1 0 1 2 3 4 5 6 7 8
。
.
.
.
.
.
.
.
.
.
.
.
.
2、你能将 的解集表示在数轴上吗?
-3 -2 -1 0 1 2 3 4 5 6 7 8
不等式 的解集可以用数轴上表示4的点的左边部分来表示。在数轴上表示4的点的位置上画实心圆点,表示4在这个解集内。
做一做 再观察
A同学:
D同学:
C同学:
B同学:
各小组内的每一名同学动手分别在数轴上作出下列解集,再观察有什么特点?
交流、总结在数轴上作不等式解集的步骤
用数轴表示不等式的解集通常分成三步进行,
即“画数轴、定界点、走方向”;
1、画数轴:原点、正方向、单位长度
3、走方向:指示线的方向,“>”向右,“<”向左
2、定界点:有“=”用实心点,没有“=”用空心圈
归纳总结
根据下列数轴上的解集,请写出不等式的解集:
2、 ≤-1;
试试看 你能行
1、 >4
3、
4、
例2、求不等式 的解集,并把它的解集表示
在数轴上,求出解集中的非负正整数解。
解:根据不等式的基本性质1,两边都加上2,
得-2 >-8
根据不等式的基本性质3,两边都除以-2,得 <4
所以:原不等式的非负正整数解为: 0,1,2,3
已知方程 的解是 =3,
求 不等式的解集。
解:由方程 的解是 ,
得,
当 时,不等式
所以:
当堂检测
本节课你有什么感受和收获?
1、什么是不等式的解,不等式的解集,解不等式;
2、会探索简单不等式的解集,并把解集表示在数轴上;
3、用数轴表示不等式解集时的一般步骤:“画数轴、定界点、走方向”以及注意事项。
课后训练 巩固提高
教材P44“习题2.3”
第2、3题
谢谢!
认知目标:不等式的解集的两种表示方法.
学习目标
理解目标:求不等式的整数解.
运用目标:求不等式的解集并能在数轴上表示出来.
温故知新,情景引入
请你说一说不等式的基本性质的内容
性质1:不等式的两边都加上(或减去)同一个整式, 不等号的方向不变.
性质2:不等式的两边都乘以(或除以)
同一个正数,不等号的方向不变.
性质3:不等式的两边都乘以(或除以)同一个负数,不等号的方向改变.
2.方程的解的定义是什么?
使得方程中等号两边相等的未知数的值叫做方程的解;
3.类似地,你认为什么是不等式的解?
类比思考
燃放某种烟花时,为了确保安全,人在
点燃导火线后要在燃放前转移到10m以外
的安全区域。已知导火线的燃烧速度为
0.02m/s,人离开的速度为4m/s,那么导
火线的长度应满足什么条件?
观各抒己见
1、算数方法
燃放者离开时间要多于: 秒;
引火线的长度要大于: 米
设引火线的长度为 时,燃放者在燃放前刚好可以转移到 处
2、利用方程
所以:引火线的长度要大于5厘米。
合作学习
3、利用不等式
解:设引火线的长度为 时,根据题意,得
根据不等式的基本性质,得
所以,引火线的长度应大于5cm
1.x=4、5、6、8能使不等式x>5成立么?
x
2.你还能说出几个使不等式x>5成立的 值吗?你认为不等式x>5的解有几个?它们有什么特点?
3.你能说出使不等式x2≤0成立的x值吗?
探究1:不等式的解、解集的概念。
=6、8能使不等式 x >5成立
x =9、10、11……,有无数个,它们都比5大
x=0
归纳结论
不等式的解:能使不等式成立的未知数的值;
不等式的解集:
一个含有未知数的不等式的所有解;
例如, =3.5、4、5、5.5都是不等式 的解
什么叫解不等式?
可类比什么叫解方程 ?
求不等式的解集的过程,叫做解不等式。
讨论
(1) 不等式 的解有多少个?
(2)不等式的解与方程的解有什么不同?
无数个
不等式的解是一个范围,而方程的解是固定个数限制的,如:一次方程的解是一个,二次方程的解是两个等等
例1、
下列说法中,错误的是( )
A、不等式 <2的正整数解有一个
B、-2是不等式2 -1<0的一个解
C、不等式-3 >9的解集是 >-3
D、不等式 <10的整数解有无数个
C
探究2:在数轴上表示不等式的解集。
1、 是不是 的解, 呢?你能用自己的方式将 的解集表示在数轴上吗?
不等式 的解集可以用数轴上表示5的点的右边部分来表示。在数轴上表示5的点的位置上画空心圆圈,表示5不在这个解集内。
-3 -2 -1 0 1 2 3 4 5 6 7 8
。
.
.
.
.
.
.
.
.
.
.
.
.
2、你能将 的解集表示在数轴上吗?
-3 -2 -1 0 1 2 3 4 5 6 7 8
不等式 的解集可以用数轴上表示4的点的左边部分来表示。在数轴上表示4的点的位置上画实心圆点,表示4在这个解集内。
做一做 再观察
A同学:
D同学:
C同学:
B同学:
各小组内的每一名同学动手分别在数轴上作出下列解集,再观察有什么特点?
交流、总结在数轴上作不等式解集的步骤
用数轴表示不等式的解集通常分成三步进行,
即“画数轴、定界点、走方向”;
1、画数轴:原点、正方向、单位长度
3、走方向:指示线的方向,“>”向右,“<”向左
2、定界点:有“=”用实心点,没有“=”用空心圈
归纳总结
根据下列数轴上的解集,请写出不等式的解集:
2、 ≤-1;
试试看 你能行
1、 >4
3、
4、
例2、求不等式 的解集,并把它的解集表示
在数轴上,求出解集中的非负正整数解。
解:根据不等式的基本性质1,两边都加上2,
得-2 >-8
根据不等式的基本性质3,两边都除以-2,得 <4
所以:原不等式的非负正整数解为: 0,1,2,3
已知方程 的解是 =3,
求 不等式的解集。
解:由方程 的解是 ,
得,
当 时,不等式
所以:
当堂检测
本节课你有什么感受和收获?
1、什么是不等式的解,不等式的解集,解不等式;
2、会探索简单不等式的解集,并把解集表示在数轴上;
3、用数轴表示不等式解集时的一般步骤:“画数轴、定界点、走方向”以及注意事项。
课后训练 巩固提高
教材P44“习题2.3”
第2、3题
谢谢!
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
