北师大版八年级下册数学3.1《直角坐标系中图形的平移与坐标的变化》课件 (共20张PPT)
文档属性
| 名称 | 北师大版八年级下册数学3.1《直角坐标系中图形的平移与坐标的变化》课件 (共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 724.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-17 16:28:06 | ||
图片预览



文档简介
一、复习旧知,铺垫新知(6分钟)
1.什么叫平移?
2.图形的平移有哪些性质?
在平面内,把一个图形整体沿某一直线方向移动一定的距离,会得到一个新图形. 图形的这种移动叫做平移.
(1)新图形与原图形形状和大小完全相同;
位置不同.
(2)对应点的连线平行且相等.
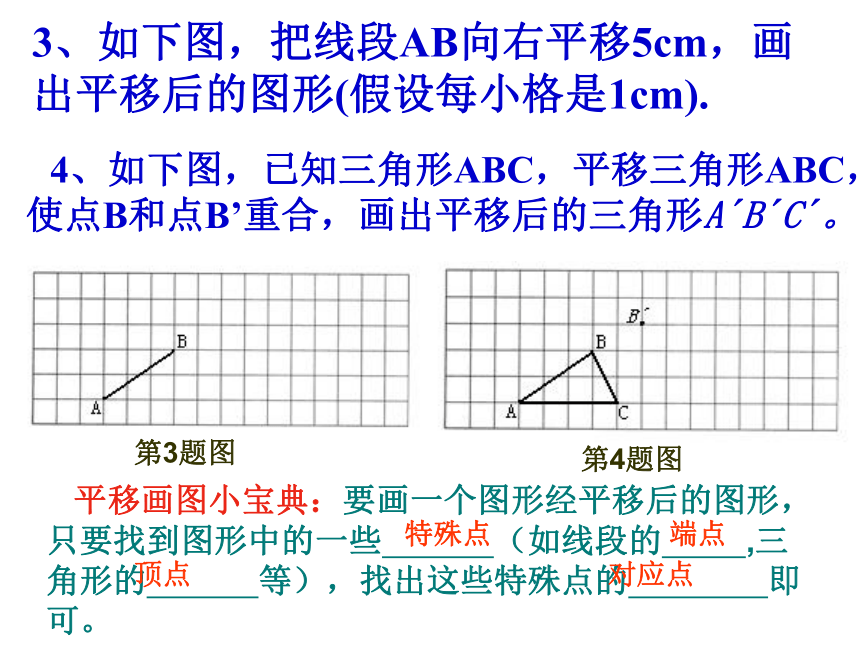
3、如下图,把线段AB向右平移5cm,画出平移后的图形(假设每小格是1cm).
4、如下图,已知三角形ABC,平移三角形ABC,使点B和点B’重合,画出平移后的三角形A?B?C?。
平移画图小宝典:要画一个图形经平移后的图形,只要找到图形中的一些 (如线段的 ,三角形的 等),找出这些特殊点的 即可。
第3题图
第4题图
特殊点
端点
顶点
对应点
用坐标表示平移
北师大版八年级(下册)第三章第2节
二、合作交流,探究新知(10分钟)
(1,-1)
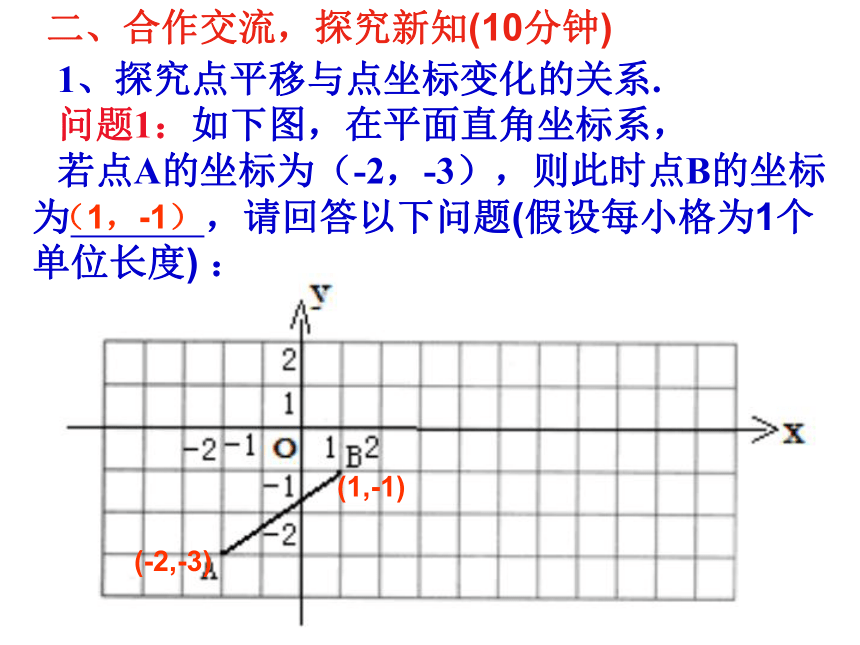
1、探究点平移与点坐标变化的关系.
问题1:如下图,在平面直角坐标系,
若点A的坐标为(-2,-3),则此时点B的坐标为 ,请回答以下问题(假设每小格为1个单位长度) :
(-2,-3)
(1,-1)
二、合作交流,探究新知(5分钟)
(3,-3)
(-5,-3)
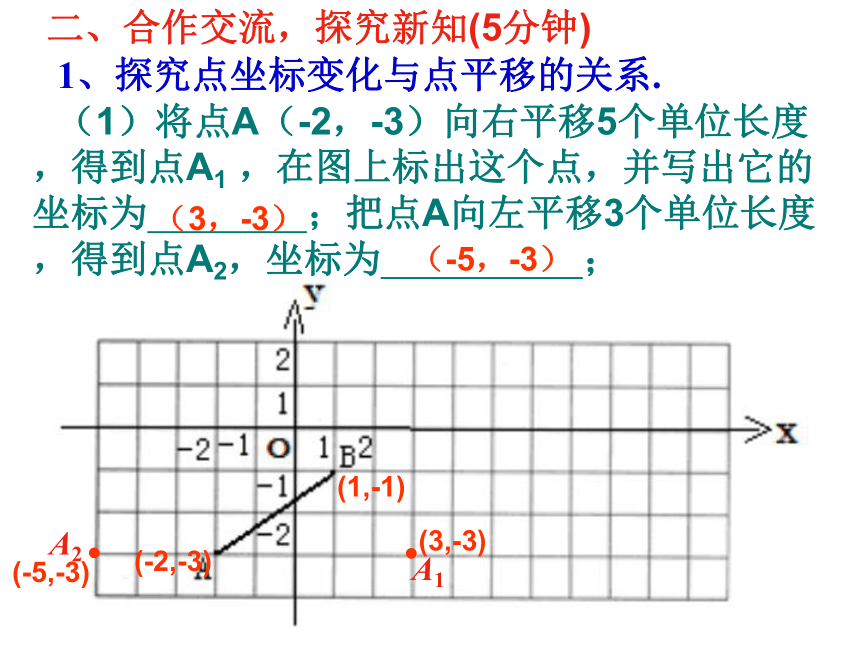
1、探究点坐标变化与点平移的关系.
(1)将点A(-2,-3)向右平移5个单位长度,得到点A1 ,在图上标出这个点,并写出它的坐标为 ;把点A向左平移3个单位长度,得到点A2,坐标为 ;
A1
?
?
A2
(-2,-3)
(3,-3)
(-5,-3)
(1,-1)
二、合作交流,探究新知(5分钟)
A1
?
?
A2
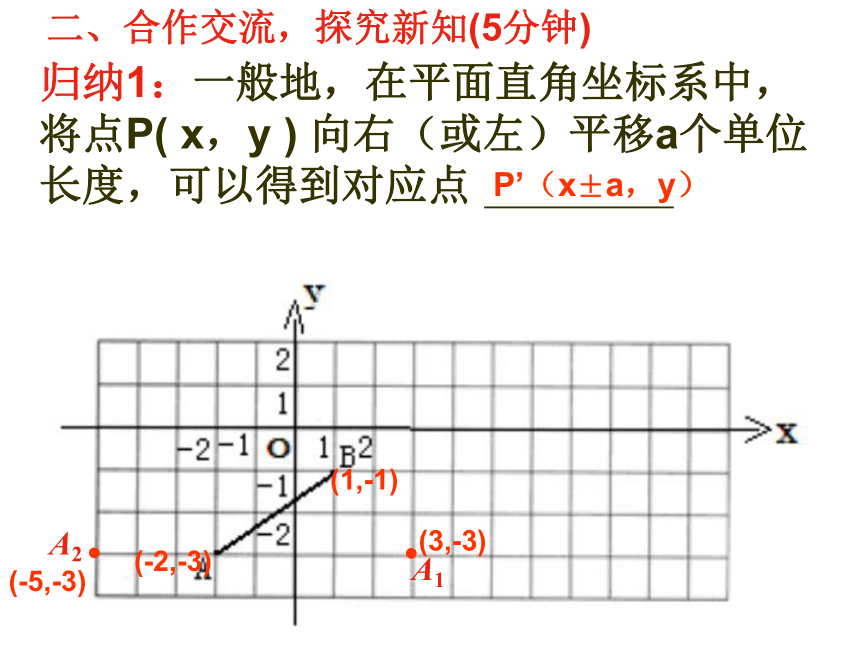
归纳1:一般地,在平面直角坐标系中,将点P( x,y ) 向右(或左)平移a个单位长度,可以得到对应点
P’(x±a,y)
(-2,-3)
(3,-3)
(-5,-3)
(1,-1)
二、合作交流,探究新知(5分钟)
(-2,-1)
(-2,-4)
?
A4
A3
?
1、探究点坐标变化与点平移的关系.
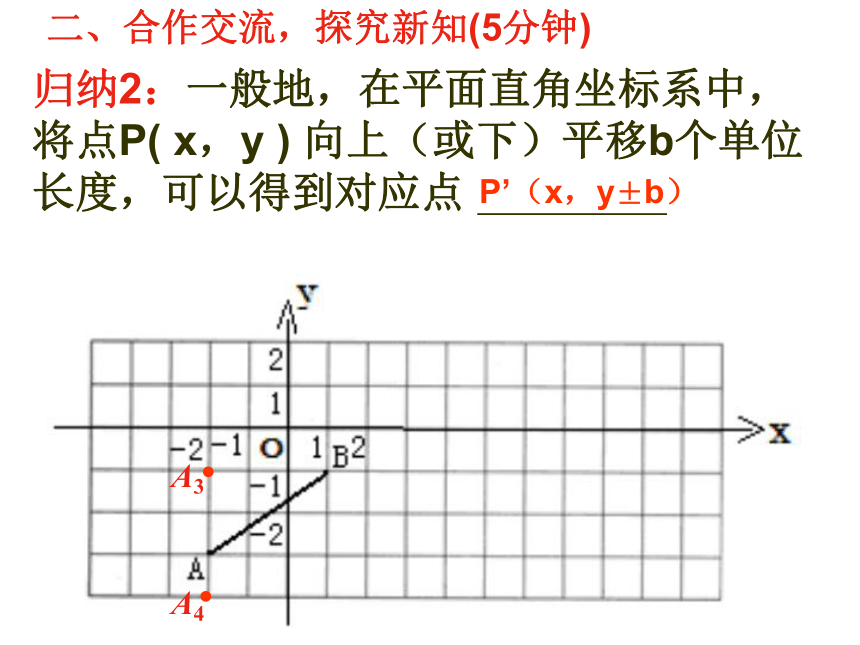
(2)将点A(-2,-3)向上平移2个单位长度,得到点A3 ,在图上标出这个点,并写出它的坐标为 ;把点A向下平移1个单位长度,得到点A4,坐标为 ;
(-2,-3)
(-2,-1)
(-2,-4)
(1,-1)
二、合作交流,探究新知(5分钟)
?
A4
A3
?
归纳2:一般地,在平面直角坐标系中,将点P( x,y ) 向上(或下)平移b个单位长度,可以得到对应点
P’(x,y±b)
?
A1
?
B1
?
C1
三、动手操作,感悟新知(8分钟)
2、探究图形平移与图形各个点坐标变化的关系
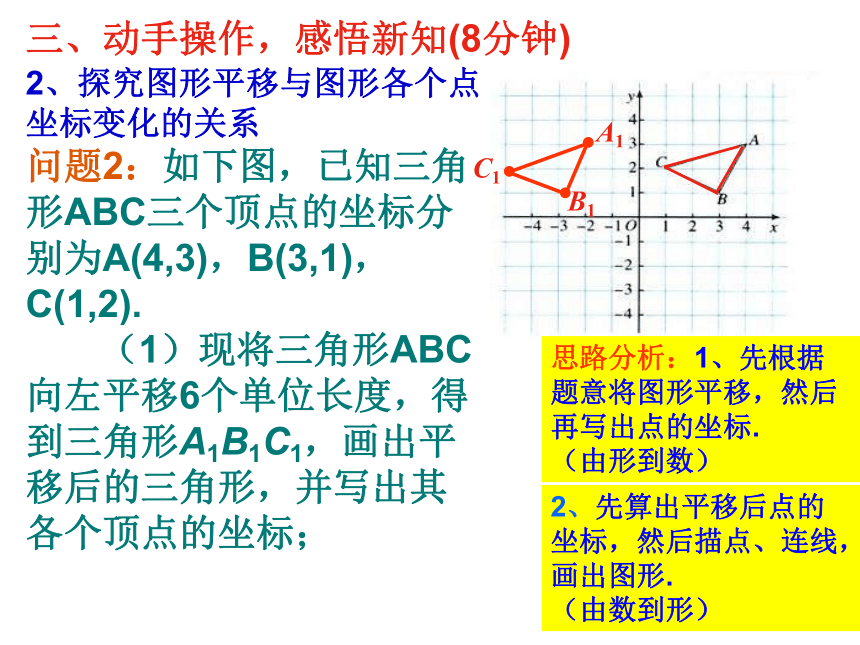
问题2:如下图,已知三角形ABC三个顶点的坐标分别为A(4,3),B(3,1),C(1,2).
(1)现将三角形ABC向左平移6个单位长度,得到三角形A1B1C1,画出平移后的三角形,并写出其各个顶点的坐标;
思路分析:1、先根据题意将图形平移,然后再写出点的坐标.
(由形到数)
2、先算出平移后点的坐标,然后描点、连线,画出图形.
(由数到形)
?
A2
?
B2
?
C2
三、动手操作,感悟新知(3分钟)
2、探究图形平移与图形各个点坐标变化的关系
问题2:如下图,已知三角形ABC三个顶点的坐标分别为A(4,3),B(3,1),C(1,2).
(2)现将三角形ABC向下平移5个单位长度,得到三角形A2B2C2,画出平移后的三角形,并写出其各个顶点的坐标;
?
?
?
三、动手操作,感悟新知(3分钟)
2、探究图形平移与图形各个点坐标变化的关系
问题2:如下图,已知三角形ABC三个顶点的坐标分别为A(4,3),B(3,1),C(1,2).
现将三角形ABC先向左平移6个单位长度,再向下平移5个单位长度,得到三角形A3B3C3,画出平移后的三角形,并写出其各个顶点的坐标;
B3
C3
A3
思考1:如果直接平移三角形ABC,使点A移到点A3 ,它和我们前面得到的三角形A3B3C3 的位置相同吗?
?
?
?
三、动手操作,感悟新知(3分钟)
2、探究图形平移与图形各个点坐标变化的关系
问题2:如下图,已知三角形ABC三个顶点的坐标分别为A(4,3),B(3,1),C(1,2).
(3)现将三角形ABC先向左平移6个单位长度,再向下平移5个单位长度,得到三角形A3B3C3,画出平移后的三角形,并写出其各个顶点的坐标;
B3
C3
A3
一般地,将一个图形依次沿两个坐标轴方向平移所得到的图形,可以通过将原来的图形作一次平移得到。
?
?
?
三、动手操作,感悟新知(3分钟)
2、探究图形平移与图形各个点坐标变化的关系
问题2:如下图,已知三角形ABC三个顶点的坐标分别为A(4,3),B(3,1),C(1,2).
(3)现将三角形ABC先向左平移6个单位长度,再向下平移5个单位长度,得到三角形A3B3C3,画出平移后的三角形,并写出其各个顶点的坐标;
B3
C3
A3
思考2:若三角形ABC上某一点的坐标为P(a,b),则经此平移后其对应点的坐标为 .
(a-6,b-5)
(3)将点A(5,-1)先向下平移3个单位长度,再向右平移2个单位长度得到点A3,坐标为_____.
(2)将点A(5,-1)向左平移2个单位长度,得到点A2,坐标为_____;
四、巩固练习,运用新知(10分钟)
1、(1)将点A(5,-1)向上平移2个单位长度,得到点A1,坐标为_____;
(5,1)
(3,-1)
(7,-4)
2、将点A(4,3)向 平移 个单位长度后,其坐标变为( 6, 3 ).
右
2
3、三角形ABC中,BC边上的中点为M,把三角形 ABC向右平移2个单位长度,再向下平移3个单位长度后,得到三角形A1 B1 C1,边
B1 C1的中点M1的坐标为(-1,0),则点M的坐标为 .
四、巩固练习,运用新知(10分钟)
(-3,3)
四、巩固练习,运用新知(10分钟)
4、将平行四边形ABCD向左平移2个单位长度,然后再向上平移3个单位长度,可以得到平行四边形A?B?C?D?。
(1)画出平移后的图形,并指出其各个顶点的坐标;
思路分析:1、先根据题意将图形平移,然后再写出点的坐标.(由形到数)
2、先算出平移后点的坐标,然后描点、连线,画出图形.
(由数到形)
四、巩固练习,运用新知(10分钟)
4、将平行四边形ABCD向左平移2个单位长度,然后再向上平移3个单位长度,可以得到平行四边形A?B?C?D?。
(1)画出平移后的图形,并指出其各个顶点的坐标;
(2)若平行四边形ABCD上某一点的坐标为
Q(m,n),则经平移后对应点的坐标为 .
(m-2,n+3)
五、归纳小结,布置作业(6分钟)
课堂小结:
1、这节课你学到了什么知识?
2、在本节课的学习活动过程中,你有何体会?
3、你还有什么想法吗?
布置课后作业:
1、必做题:课本第73-74页习题3.3
第2、3、4题;
2、选做题:课本第74页第5题.
(1)左、右平移:
向右平移a个单位
(2)上、下平移:
原图形上的点(x,y) ,
向左平移a个单位
原图形上的点(x,y) ,
(x+a,y)
(x-a,y)
向上平移b个单位
原图形上的点(x,y) ,
向下平移b个单位
原图形上的点(x,y) ,
(x,y+b)
(x,y-b)
归纳:一般地,在平面直角坐标系中,图形平移时点坐标的变化规律
同学们
再见!
1.什么叫平移?
2.图形的平移有哪些性质?
在平面内,把一个图形整体沿某一直线方向移动一定的距离,会得到一个新图形. 图形的这种移动叫做平移.
(1)新图形与原图形形状和大小完全相同;
位置不同.
(2)对应点的连线平行且相等.
3、如下图,把线段AB向右平移5cm,画出平移后的图形(假设每小格是1cm).
4、如下图,已知三角形ABC,平移三角形ABC,使点B和点B’重合,画出平移后的三角形A?B?C?。
平移画图小宝典:要画一个图形经平移后的图形,只要找到图形中的一些 (如线段的 ,三角形的 等),找出这些特殊点的 即可。
第3题图
第4题图
特殊点
端点
顶点
对应点
用坐标表示平移
北师大版八年级(下册)第三章第2节
二、合作交流,探究新知(10分钟)
(1,-1)
1、探究点平移与点坐标变化的关系.
问题1:如下图,在平面直角坐标系,
若点A的坐标为(-2,-3),则此时点B的坐标为 ,请回答以下问题(假设每小格为1个单位长度) :
(-2,-3)
(1,-1)
二、合作交流,探究新知(5分钟)
(3,-3)
(-5,-3)
1、探究点坐标变化与点平移的关系.
(1)将点A(-2,-3)向右平移5个单位长度,得到点A1 ,在图上标出这个点,并写出它的坐标为 ;把点A向左平移3个单位长度,得到点A2,坐标为 ;
A1
?
?
A2
(-2,-3)
(3,-3)
(-5,-3)
(1,-1)
二、合作交流,探究新知(5分钟)
A1
?
?
A2
归纳1:一般地,在平面直角坐标系中,将点P( x,y ) 向右(或左)平移a个单位长度,可以得到对应点
P’(x±a,y)
(-2,-3)
(3,-3)
(-5,-3)
(1,-1)
二、合作交流,探究新知(5分钟)
(-2,-1)
(-2,-4)
?
A4
A3
?
1、探究点坐标变化与点平移的关系.
(2)将点A(-2,-3)向上平移2个单位长度,得到点A3 ,在图上标出这个点,并写出它的坐标为 ;把点A向下平移1个单位长度,得到点A4,坐标为 ;
(-2,-3)
(-2,-1)
(-2,-4)
(1,-1)
二、合作交流,探究新知(5分钟)
?
A4
A3
?
归纳2:一般地,在平面直角坐标系中,将点P( x,y ) 向上(或下)平移b个单位长度,可以得到对应点
P’(x,y±b)
?
A1
?
B1
?
C1
三、动手操作,感悟新知(8分钟)
2、探究图形平移与图形各个点坐标变化的关系
问题2:如下图,已知三角形ABC三个顶点的坐标分别为A(4,3),B(3,1),C(1,2).
(1)现将三角形ABC向左平移6个单位长度,得到三角形A1B1C1,画出平移后的三角形,并写出其各个顶点的坐标;
思路分析:1、先根据题意将图形平移,然后再写出点的坐标.
(由形到数)
2、先算出平移后点的坐标,然后描点、连线,画出图形.
(由数到形)
?
A2
?
B2
?
C2
三、动手操作,感悟新知(3分钟)
2、探究图形平移与图形各个点坐标变化的关系
问题2:如下图,已知三角形ABC三个顶点的坐标分别为A(4,3),B(3,1),C(1,2).
(2)现将三角形ABC向下平移5个单位长度,得到三角形A2B2C2,画出平移后的三角形,并写出其各个顶点的坐标;
?
?
?
三、动手操作,感悟新知(3分钟)
2、探究图形平移与图形各个点坐标变化的关系
问题2:如下图,已知三角形ABC三个顶点的坐标分别为A(4,3),B(3,1),C(1,2).
现将三角形ABC先向左平移6个单位长度,再向下平移5个单位长度,得到三角形A3B3C3,画出平移后的三角形,并写出其各个顶点的坐标;
B3
C3
A3
思考1:如果直接平移三角形ABC,使点A移到点A3 ,它和我们前面得到的三角形A3B3C3 的位置相同吗?
?
?
?
三、动手操作,感悟新知(3分钟)
2、探究图形平移与图形各个点坐标变化的关系
问题2:如下图,已知三角形ABC三个顶点的坐标分别为A(4,3),B(3,1),C(1,2).
(3)现将三角形ABC先向左平移6个单位长度,再向下平移5个单位长度,得到三角形A3B3C3,画出平移后的三角形,并写出其各个顶点的坐标;
B3
C3
A3
一般地,将一个图形依次沿两个坐标轴方向平移所得到的图形,可以通过将原来的图形作一次平移得到。
?
?
?
三、动手操作,感悟新知(3分钟)
2、探究图形平移与图形各个点坐标变化的关系
问题2:如下图,已知三角形ABC三个顶点的坐标分别为A(4,3),B(3,1),C(1,2).
(3)现将三角形ABC先向左平移6个单位长度,再向下平移5个单位长度,得到三角形A3B3C3,画出平移后的三角形,并写出其各个顶点的坐标;
B3
C3
A3
思考2:若三角形ABC上某一点的坐标为P(a,b),则经此平移后其对应点的坐标为 .
(a-6,b-5)
(3)将点A(5,-1)先向下平移3个单位长度,再向右平移2个单位长度得到点A3,坐标为_____.
(2)将点A(5,-1)向左平移2个单位长度,得到点A2,坐标为_____;
四、巩固练习,运用新知(10分钟)
1、(1)将点A(5,-1)向上平移2个单位长度,得到点A1,坐标为_____;
(5,1)
(3,-1)
(7,-4)
2、将点A(4,3)向 平移 个单位长度后,其坐标变为( 6, 3 ).
右
2
3、三角形ABC中,BC边上的中点为M,把三角形 ABC向右平移2个单位长度,再向下平移3个单位长度后,得到三角形A1 B1 C1,边
B1 C1的中点M1的坐标为(-1,0),则点M的坐标为 .
四、巩固练习,运用新知(10分钟)
(-3,3)
四、巩固练习,运用新知(10分钟)
4、将平行四边形ABCD向左平移2个单位长度,然后再向上平移3个单位长度,可以得到平行四边形A?B?C?D?。
(1)画出平移后的图形,并指出其各个顶点的坐标;
思路分析:1、先根据题意将图形平移,然后再写出点的坐标.(由形到数)
2、先算出平移后点的坐标,然后描点、连线,画出图形.
(由数到形)
四、巩固练习,运用新知(10分钟)
4、将平行四边形ABCD向左平移2个单位长度,然后再向上平移3个单位长度,可以得到平行四边形A?B?C?D?。
(1)画出平移后的图形,并指出其各个顶点的坐标;
(2)若平行四边形ABCD上某一点的坐标为
Q(m,n),则经平移后对应点的坐标为 .
(m-2,n+3)
五、归纳小结,布置作业(6分钟)
课堂小结:
1、这节课你学到了什么知识?
2、在本节课的学习活动过程中,你有何体会?
3、你还有什么想法吗?
布置课后作业:
1、必做题:课本第73-74页习题3.3
第2、3、4题;
2、选做题:课本第74页第5题.
(1)左、右平移:
向右平移a个单位
(2)上、下平移:
原图形上的点(x,y) ,
向左平移a个单位
原图形上的点(x,y) ,
(x+a,y)
(x-a,y)
向上平移b个单位
原图形上的点(x,y) ,
向下平移b个单位
原图形上的点(x,y) ,
(x,y+b)
(x,y-b)
归纳:一般地,在平面直角坐标系中,图形平移时点坐标的变化规律
同学们
再见!
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
