北师大版九年级数学下册:3.9弧长与扇形面积 课件 (共19张PPT)
文档属性
| 名称 | 北师大版九年级数学下册:3.9弧长与扇形面积 课件 (共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-17 09:01:04 | ||
图片预览




文档简介
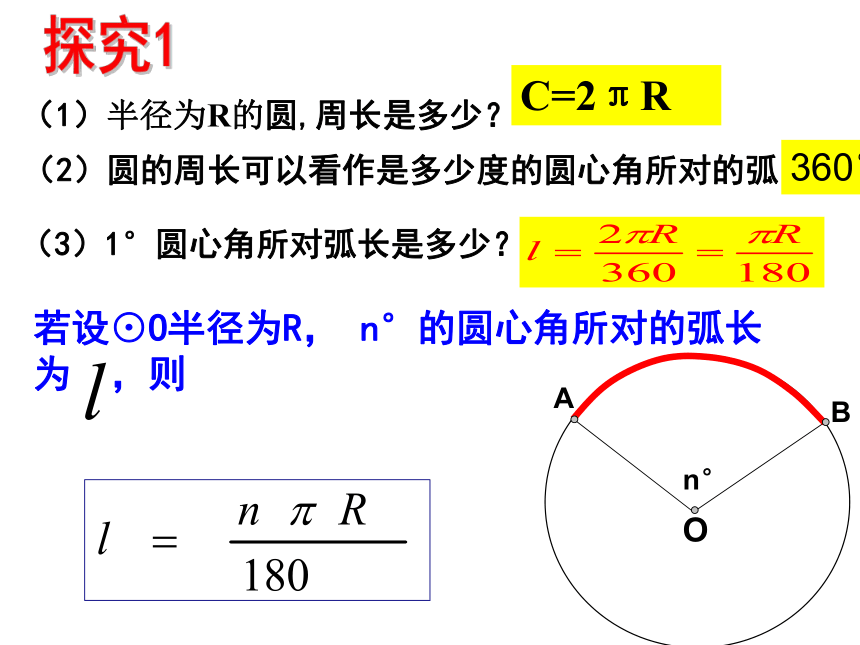
(1)半径为R的圆,周长是多少?
C=2πR
(3)1°圆心角所对弧长是多少?
(2)圆的周长可以看作是多少度的圆心角所对的弧?
n°
A
B
O
若设⊙O半径为R, n°的圆心角所对的弧长为 ,则
360°
已知圆弧的半径为50厘米,圆心角为60°,
求此圆弧的长度。
=
(cm)
答:此圆弧的长度为
cm
解:
1、在半径为24的圆中,60°的圆心角所对的弧长l= ;
2、75°的圆心角所对的弧长是2.5π,则此弧所在圆的半径为 。
6
8π
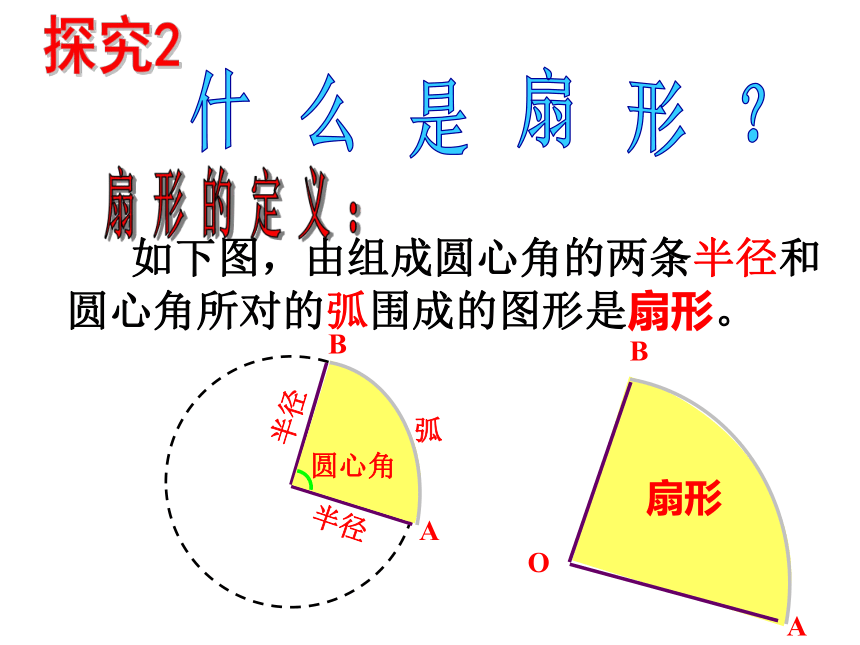
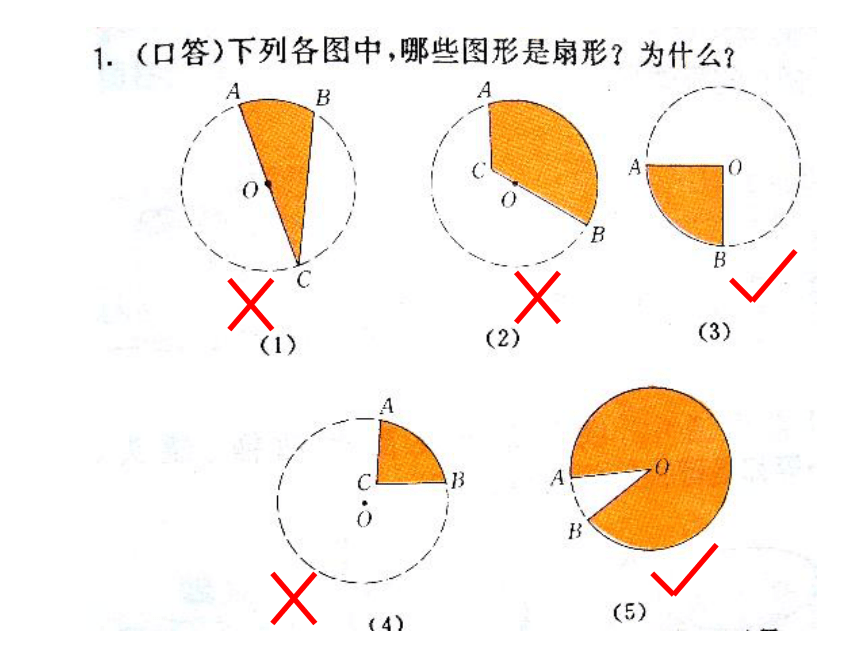
如下图,由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形。
半径
半径
圆心角
圆心角
弧
A
B
O
B
A
扇形
那么: 在半径为R 的圆中,n°的圆心角所对的扇形面积的计算公式为
如果圆的半径为R,则圆的面积为 ,
l°的圆心角对应的扇形面积为 ,
°的圆心角对应的扇形面积为
(1)若扇形的圆心角n为50°,半径为R=1,则这个扇形的面积,S扇= ;
(2)若扇形的圆心角n为60°, 面积为 ,则这个扇形的半径R= ;
(3)若扇形的半径R=3, S扇形=3π,则这个扇形的圆心角n的度数 ;
2
120°
A
B
O
O
比较扇形面积与弧长公式, 用弧长表示扇形面积:
1、若扇形的半径R=2㎝,弧长 ㎝,则这个扇形的面积,S扇= ________
弓形:由弦及其所对的弧组成的图形叫做弓形.
弦AB把圆面分成两部分,这两部分都是弓形.
0
B
A
例题:如图、水平放置的圆柱形排水管道的截面半径是12cm,其中水面高6cm,求截面上有水部分的面积。
0
B
A
C
E
有水部分的面积 = S扇- S△
练习:如图、水平放置的圆柱形排水管道的截面半径是6cm,其中水面高9cm,求截面上有水部分的面积。
0
A
B
D
C
E
变式训练
S弓形= S扇形+S△
感悟:
(1)当弓形面积小于半圆时
S弓形= S扇形-S△
(2)当弓形面积大于半圆时
S弓形= S扇形+S△
(3)当弓形面积等于半圆时
S弓形= S半圆
课后作业:
D
B
B
D
D
第6题
第7题
变式
B
4Π
Π/2
第8题
变式
2. 扇形面积公式与弧长公式的区别:
S扇形= S圆
360
n
L弧= C圆
360
n
1. 扇形的面积大小与哪些因素有关?
(1)与圆心角的大小有关
(2)与半径的长短有关
3.弓形面积:
(1)当弓形面积小于半圆时S弓形= S扇形-S△
(2)当弓形面积大于半圆时S弓形= S扇形+S△
(3)当弓形面积等于半圆时 S弓形= S半圆
= πR
180
n
360
n
= πR2
1
=
-
2
RL
C=2πR
(3)1°圆心角所对弧长是多少?
(2)圆的周长可以看作是多少度的圆心角所对的弧?
n°
A
B
O
若设⊙O半径为R, n°的圆心角所对的弧长为 ,则
360°
已知圆弧的半径为50厘米,圆心角为60°,
求此圆弧的长度。
=
(cm)
答:此圆弧的长度为
cm
解:
1、在半径为24的圆中,60°的圆心角所对的弧长l= ;
2、75°的圆心角所对的弧长是2.5π,则此弧所在圆的半径为 。
6
8π
如下图,由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形。
半径
半径
圆心角
圆心角
弧
A
B
O
B
A
扇形
那么: 在半径为R 的圆中,n°的圆心角所对的扇形面积的计算公式为
如果圆的半径为R,则圆的面积为 ,
l°的圆心角对应的扇形面积为 ,
°的圆心角对应的扇形面积为
(1)若扇形的圆心角n为50°,半径为R=1,则这个扇形的面积,S扇= ;
(2)若扇形的圆心角n为60°, 面积为 ,则这个扇形的半径R= ;
(3)若扇形的半径R=3, S扇形=3π,则这个扇形的圆心角n的度数 ;
2
120°
A
B
O
O
比较扇形面积与弧长公式, 用弧长表示扇形面积:
1、若扇形的半径R=2㎝,弧长 ㎝,则这个扇形的面积,S扇= ________
弓形:由弦及其所对的弧组成的图形叫做弓形.
弦AB把圆面分成两部分,这两部分都是弓形.
0
B
A
例题:如图、水平放置的圆柱形排水管道的截面半径是12cm,其中水面高6cm,求截面上有水部分的面积。
0
B
A
C
E
有水部分的面积 = S扇- S△
练习:如图、水平放置的圆柱形排水管道的截面半径是6cm,其中水面高9cm,求截面上有水部分的面积。
0
A
B
D
C
E
变式训练
S弓形= S扇形+S△
感悟:
(1)当弓形面积小于半圆时
S弓形= S扇形-S△
(2)当弓形面积大于半圆时
S弓形= S扇形+S△
(3)当弓形面积等于半圆时
S弓形= S半圆
课后作业:
D
B
B
D
D
第6题
第7题
变式
B
4Π
Π/2
第8题
变式
2. 扇形面积公式与弧长公式的区别:
S扇形= S圆
360
n
L弧= C圆
360
n
1. 扇形的面积大小与哪些因素有关?
(1)与圆心角的大小有关
(2)与半径的长短有关
3.弓形面积:
(1)当弓形面积小于半圆时S弓形= S扇形-S△
(2)当弓形面积大于半圆时S弓形= S扇形+S△
(3)当弓形面积等于半圆时 S弓形= S半圆
= πR
180
n
360
n
= πR2
1
=
-
2
RL
