北师大版九年级数学下册3.9: 弧长及扇形的面积课件 (共22张PPT)
文档属性
| 名称 | 北师大版九年级数学下册3.9: 弧长及扇形的面积课件 (共22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 540.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-17 00:00:00 | ||
图片预览






文档简介
第三章 圆
第9节 弧长及扇形的面积
学习目标
一、弧长公式的推导与运用
二、扇形面积公式的推导与运用
复习旧知
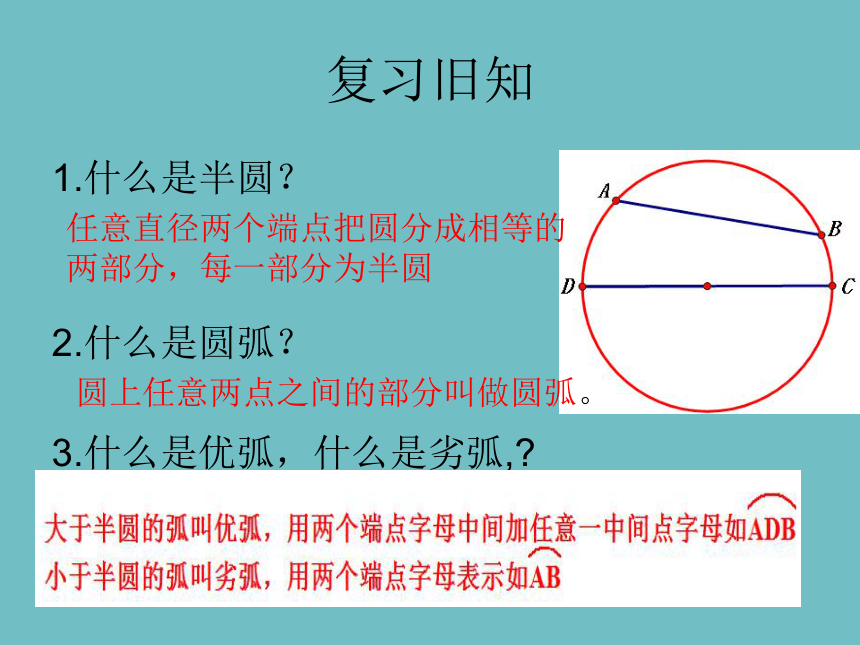
1.什么是半圆?
2.什么是圆弧?
3.什么是优弧,什么是劣弧,?
任意直径两个端点把圆分成相等的两部分,每一部分为半圆
圆上任意两点之间的部分叫做圆弧。
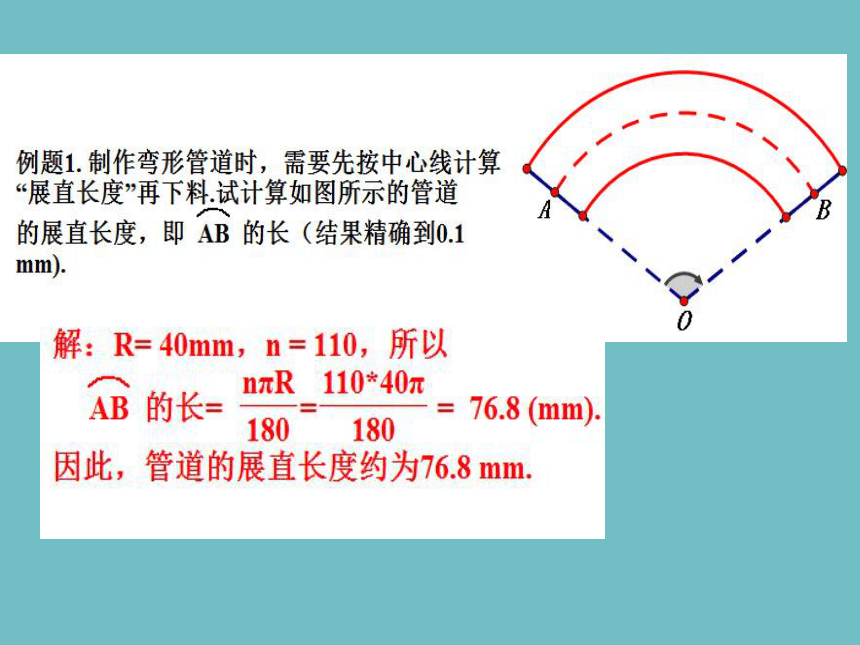
如图3-37,某传送带的一个转动轮的半径为10cm。
(1)转动轮转一周,传送带上的物品A被传送多少厘米?
(2)转动轮转1°,传送带上的物品A被传送多少厘米?
(3)转动轮转n°,传送带上的物品A被传送了多少厘米?
弧长公式小结
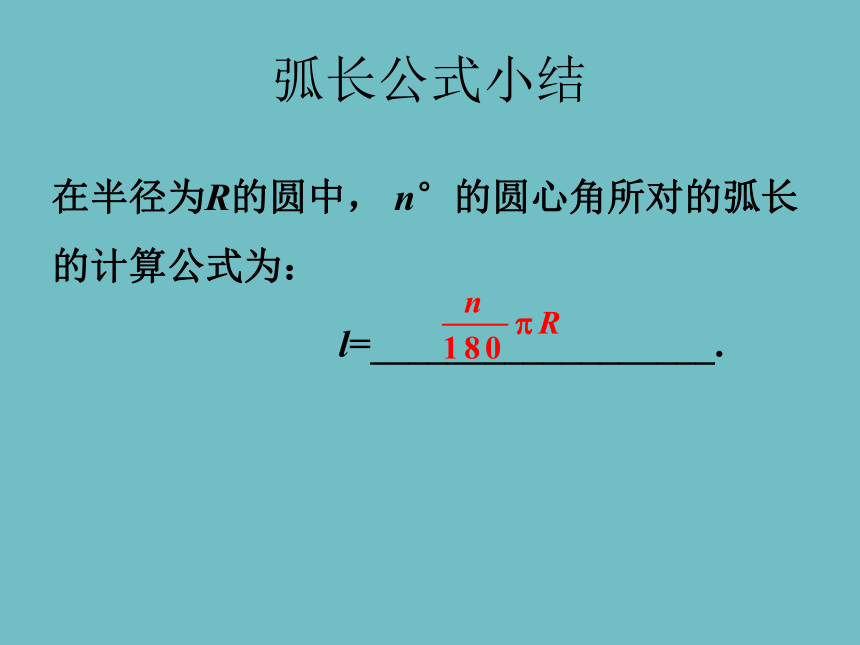
在半径为R的圆中, n°的圆心角所对的弧长的计算公式为:
l=__________________.
1.弧、弧长、弧的度数间的关系:
弧相等表示弧长、弧的度数都相等;
度数相等的弧,弧长不一定相等;
弧长相等的弧,弧的度数不一定相等.
2.易错警示:在弧长公式 l= 中,n表示1°的n倍,180表示1°的180倍,n,180不带单位.
如图,⊙O的半径为6 cm,直线AB是⊙O的
切线,切点为点B,弦BC∥AO,若∠A=30°,则劣
弧BC的长为________.
例2
导引:
由切线性质可知∠OBA=90°.因为∠A=30°,所以
∠BOA=60°,因为BC∥AO,所以∠CBO=60°.又因
为OB=OC,所以△OBC为等边三角形,所以∠BOC=
60°,代入公式l= =2π(cm).
2π cm
如图,某田径场的周长(内圈)为400 m,其中两个弯道内圈(半圆形)共长 200 m,直线段共长200 m,而每条跑道宽约1 m (共6条跑道).
(1) 内圈弯道半径为多少米?(结果精确到0.1 m)
一个内圈弯道与一个外圈弯道的长相差多少米?
(结果精确到0.1 m)
1
解:
(1)设内圈弯道的半径为r m.由题意知 ×2πr=100.
解得r≈31.8.∴内圈弯道的半径约为31.8 m.
(2)设外圈弯道的半径为R m.
∵共有6条跑道,故外圈弯道的半径R=
∴一个外圈弯道的弧长为
×2πR=πR=π =(100+6π)(m).
∴一个内圈弯道与一个外圈弯道的长相差约
100+6π-100=6π≈18.8(m).
【中考】在在半径为9的⊙O中,120°圆心角所对的弧长是( )
A.π B.2π
C.4π D.6π
2
D
【中考】如图,⊙O是△ABC的外接圆,BC=1,∠BAC=30°,则BC的长等于( )
A.
B.
C.
D.
3
︵
B
【中考】如图,在?ABCD中,∠B=70°,BC=6,以AD为直径的⊙O交CD于点E,则DE的长为( )
A. π
B. π
C. π
D. π
4
︵
B
在一块空旷的草地上有一根柱子,柱子上拴着 一条长
3 m的绳子,绳子的另一端拴着一只狗.
(1)这只狗的最大活动区域有多大?
(2)如果这只狗只能绕柱子转过n°角,
那么它的最大活动区域有多大?
扇形面积公式
1.半径为R的圆,面积是多少?
2.圆面可以看作是多少度的圆心角所对的扇形?
3.1°圆心角所对扇形面积是多少?
1. S=πR2
2. 360°
3.
若设⊙O半径为R, n°的圆
心角所对的扇形面积为S,则
A
B
O
思考1:
比较扇形面积公式与弧长公式,可以用弧长表示扇形面积:
其中l为扇形的弧长,R为半径.
扇形AOB的半径为12 cm, ∠ AOB=120°,求
的长(结果精确到 0.1 cm)和扇形AOB的面积(结果精
确到0.1 cm2).
例3
解:
的长= 25.1 ( cm).
S扇形= 150.7 (cm2 ).
因此, 的长约为25.1 cm,扇形AOB的面积约
为150.7 cm2.
如图,水平放置的一个油管的横截面半径为12 cm,
其中有油的部分油面高 6cm,求截面上有油部分的
面积(结果精确到0.1 cm2).
1
解:
如图,连接OA,OB. 设OC⊥AB于点C,交圆O于点D.
∵CD=6 cm,OD=OA=12 cm,∴OC=12-6=6(cm).在Rt△AOC中,
AC=
∴AB=12 cm,cos ∠COA=
∴∠COA=60°. ∴∠AOB=120°.
∴截面上有油部分的面积为S扇形AOB-S△AOB
= ≈88.4(cm2).
【中考】如图,正方形ABCD内接于半径为4的⊙O,则图中阴影部分的面积为( )
A.4π+14
B.4π+8
C.4π-4
D.4π-8
2
D
【中考·桂林】如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA,ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分的面积是( )
A.π
B.
C.3+π
D.8-π
3
D
通过本课时的学习,需要我们掌握:
1.弧长的计算公式l= 并运用公式进行计算.
2.扇形的面积公式S= 并运用公式进行计算.
3.弧长l及扇形的面积S之间的关系,
课堂小结
第9节 弧长及扇形的面积
学习目标
一、弧长公式的推导与运用
二、扇形面积公式的推导与运用
复习旧知
1.什么是半圆?
2.什么是圆弧?
3.什么是优弧,什么是劣弧,?
任意直径两个端点把圆分成相等的两部分,每一部分为半圆
圆上任意两点之间的部分叫做圆弧。
如图3-37,某传送带的一个转动轮的半径为10cm。
(1)转动轮转一周,传送带上的物品A被传送多少厘米?
(2)转动轮转1°,传送带上的物品A被传送多少厘米?
(3)转动轮转n°,传送带上的物品A被传送了多少厘米?
弧长公式小结
在半径为R的圆中, n°的圆心角所对的弧长的计算公式为:
l=__________________.
1.弧、弧长、弧的度数间的关系:
弧相等表示弧长、弧的度数都相等;
度数相等的弧,弧长不一定相等;
弧长相等的弧,弧的度数不一定相等.
2.易错警示:在弧长公式 l= 中,n表示1°的n倍,180表示1°的180倍,n,180不带单位.
如图,⊙O的半径为6 cm,直线AB是⊙O的
切线,切点为点B,弦BC∥AO,若∠A=30°,则劣
弧BC的长为________.
例2
导引:
由切线性质可知∠OBA=90°.因为∠A=30°,所以
∠BOA=60°,因为BC∥AO,所以∠CBO=60°.又因
为OB=OC,所以△OBC为等边三角形,所以∠BOC=
60°,代入公式l= =2π(cm).
2π cm
如图,某田径场的周长(内圈)为400 m,其中两个弯道内圈(半圆形)共长 200 m,直线段共长200 m,而每条跑道宽约1 m (共6条跑道).
(1) 内圈弯道半径为多少米?(结果精确到0.1 m)
一个内圈弯道与一个外圈弯道的长相差多少米?
(结果精确到0.1 m)
1
解:
(1)设内圈弯道的半径为r m.由题意知 ×2πr=100.
解得r≈31.8.∴内圈弯道的半径约为31.8 m.
(2)设外圈弯道的半径为R m.
∵共有6条跑道,故外圈弯道的半径R=
∴一个外圈弯道的弧长为
×2πR=πR=π =(100+6π)(m).
∴一个内圈弯道与一个外圈弯道的长相差约
100+6π-100=6π≈18.8(m).
【中考】在在半径为9的⊙O中,120°圆心角所对的弧长是( )
A.π B.2π
C.4π D.6π
2
D
【中考】如图,⊙O是△ABC的外接圆,BC=1,∠BAC=30°,则BC的长等于( )
A.
B.
C.
D.
3
︵
B
【中考】如图,在?ABCD中,∠B=70°,BC=6,以AD为直径的⊙O交CD于点E,则DE的长为( )
A. π
B. π
C. π
D. π
4
︵
B
在一块空旷的草地上有一根柱子,柱子上拴着 一条长
3 m的绳子,绳子的另一端拴着一只狗.
(1)这只狗的最大活动区域有多大?
(2)如果这只狗只能绕柱子转过n°角,
那么它的最大活动区域有多大?
扇形面积公式
1.半径为R的圆,面积是多少?
2.圆面可以看作是多少度的圆心角所对的扇形?
3.1°圆心角所对扇形面积是多少?
1. S=πR2
2. 360°
3.
若设⊙O半径为R, n°的圆
心角所对的扇形面积为S,则
A
B
O
思考1:
比较扇形面积公式与弧长公式,可以用弧长表示扇形面积:
其中l为扇形的弧长,R为半径.
扇形AOB的半径为12 cm, ∠ AOB=120°,求
的长(结果精确到 0.1 cm)和扇形AOB的面积(结果精
确到0.1 cm2).
例3
解:
的长= 25.1 ( cm).
S扇形= 150.7 (cm2 ).
因此, 的长约为25.1 cm,扇形AOB的面积约
为150.7 cm2.
如图,水平放置的一个油管的横截面半径为12 cm,
其中有油的部分油面高 6cm,求截面上有油部分的
面积(结果精确到0.1 cm2).
1
解:
如图,连接OA,OB. 设OC⊥AB于点C,交圆O于点D.
∵CD=6 cm,OD=OA=12 cm,∴OC=12-6=6(cm).在Rt△AOC中,
AC=
∴AB=12 cm,cos ∠COA=
∴∠COA=60°. ∴∠AOB=120°.
∴截面上有油部分的面积为S扇形AOB-S△AOB
= ≈88.4(cm2).
【中考】如图,正方形ABCD内接于半径为4的⊙O,则图中阴影部分的面积为( )
A.4π+14
B.4π+8
C.4π-4
D.4π-8
2
D
【中考·桂林】如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA,ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分的面积是( )
A.π
B.
C.3+π
D.8-π
3
D
通过本课时的学习,需要我们掌握:
1.弧长的计算公式l= 并运用公式进行计算.
2.扇形的面积公式S= 并运用公式进行计算.
3.弧长l及扇形的面积S之间的关系,
课堂小结
