北师大版九年级数学下册2.4二次函数的综合与应用 课件(共34张PPT)
文档属性
| 名称 | 北师大版九年级数学下册2.4二次函数的综合与应用 课件(共34张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 46.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-17 00:00:00 | ||
图片预览

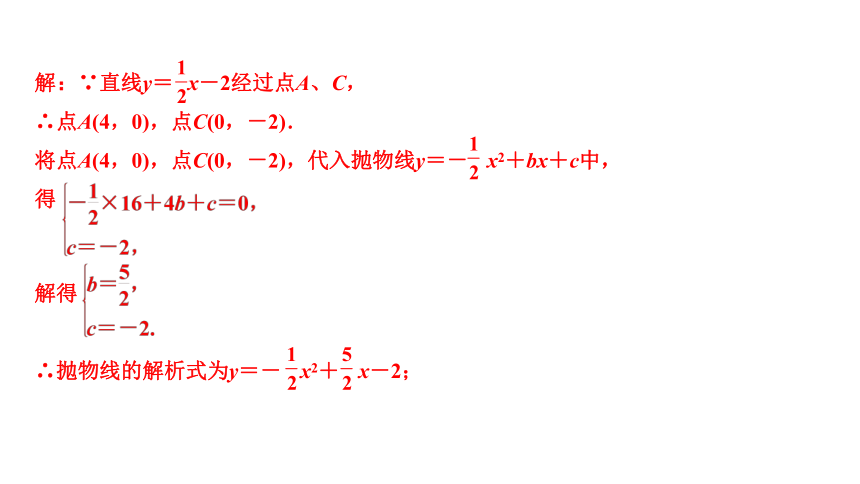







文档简介
第12讲 二次函数的综合与应用
(必考,1~2道,解答题必考1道)
类型一 与线段有关的问题
重难点突破
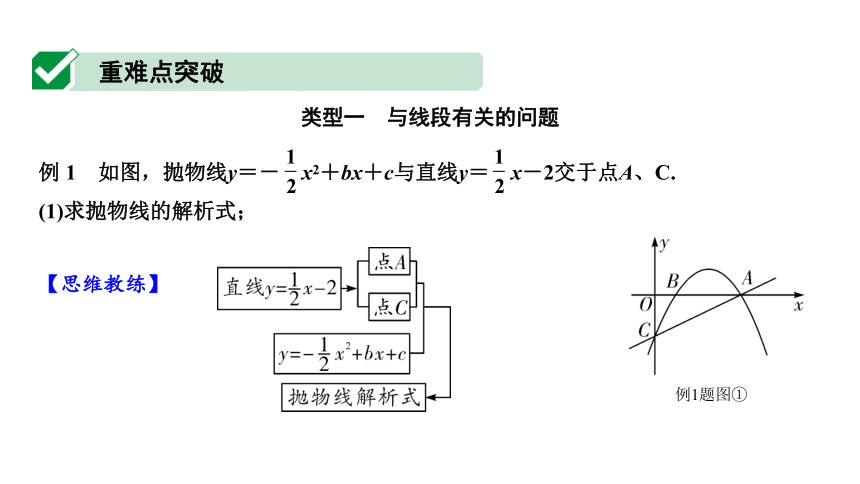
例 1 如图,抛物线y=- x2+bx+c与直线y= x-2交于点A、C.
(1)求抛物线的解析式;
例1题图①
【思维教练】
解:∵直线y= x-2经过点A、C,
∴点A(4,0),点C(0,-2).
将点A(4,0),点C(0,-2),代入抛物线y=- x2+bx+c中,
得
解得
∴抛物线的解析式为y=- x2+ x-2;
(2)设点E为x轴上一点,当AE=CE时,求点E的坐标;
【思维教练】设出点E的坐标,表示出AE的长,CE的长可利用勾股定理表示,联立方程即可求出点E的坐标.
如解图①,由点E在x轴上,可设点E的坐标为(e,0),连接CE,则AE=4-e.
在Rt△COE中,根据勾股定理得CE2=OC2+OE2=(-2)2+e2=22+e2,
∵AE=CE,
∴(4-e)2=22+e2,解得e= ,则点E的坐标为( ,0);
例1题解图①
(3)设点P为位于直线AC上方抛物线上一动点,过点P作y轴的平行线交直线AC于点H,①求当PH值最大时,点P的坐标;②过点P作PD⊥AC,求PD的最大值;
例1题图②
【思维教练】①
②要求PD的最大值,不能直接用P,D坐标表示PD的长,可通过PH的长和锐角函数值来表示PD的长,通过二次函数的性质即可求得最值.
①设点P(x,- x2+ x-2),则H(x, x-2),
∴PH=- x2+ x-2- x+2
=- x2+2x=- (x-2)2+2,且0<x<4,
∴当x=2时,PH值最大,最大值为2,
∴当PH值最大时,点P为(2,1);
②如解图②,由①知,PH=- (x-2)2+2,且0<x<4,
∴PD=PH·sin∠PHD=PH·sin∠OCA= PH=- (x-2)2+ ,
∴当x=2时,PD有最大值 ;
例1题解图②
(4)在抛物线对称轴l上是否存在一点F,使得△BCF的周长最小,若存在,求出点F的坐标及△BCF周长的最小值;若不存在,请说明理由.
【思维教练】因为BC长为定值,要使△BCF周长最小,即要使CF+BF的值最小,由点A、B关于对称轴l对称,可知AC与对称轴l的交点即为点F,即可使CF+BF最小.
存在.要使△BCF的周长最小,即BC+BF+CF最小,如解图③所示.
在Rt△OBC中,OB=1,OC=2,由勾股定理得BC=
= 为定值,∴当BF+CF最小时,C△BCF最小.
∵点B与点A关于直线l对称,
∴AC与对称轴l的交点即为所求的点F,
易得抛物线y=- x2+ x-2的对称轴为直线x= ,将x= 代入y= x-2,得y= × -2=- ,
∴点F的坐标为( ,- ).
在Rt△AOC中,由AO=4,OC=2,根据勾股定理得AC= =2 ,
∴△BCF周长的最小值为BC+BF+CF=BC+AC= +2 =3 .
例1题解图③
类型二 与面积有关的问题
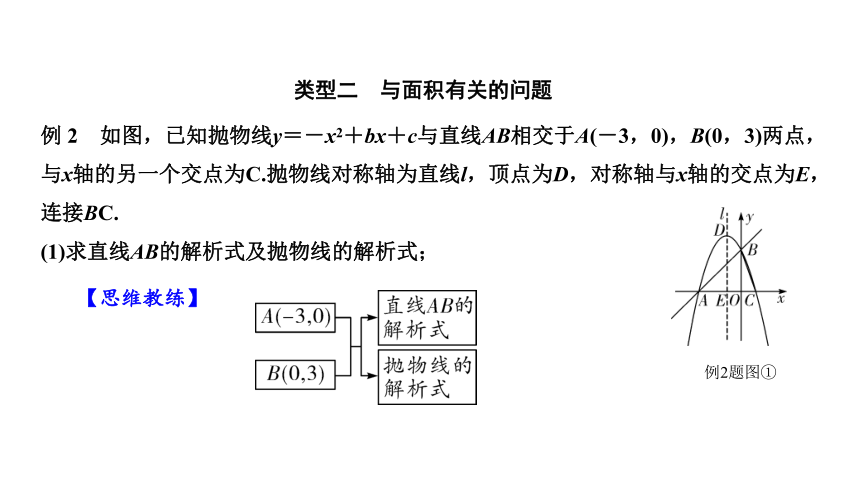
例 2 如图,已知抛物线y=-x2+bx+c与直线AB相交于A(-3,0),B(0,3)两点,与x轴的另一个交点为C.抛物线对称轴为直线l,顶点为D,对称轴与x轴的交点为E,连接BC.
(1)求直线AB的解析式及抛物线的解析式;
例2题图①
【思维教练】
解:(1)设直线AB的解析式为y=kx+d(k≠0),
将A(-3,0),B(0,3)代入,
得 解得
∴直线AB的解析式为y=x+3.
将A(-3,0),B(0,3)代入抛物线解析式y=-x2+bx+c中,
得
解得
∴抛物线的解析式为y=-x2-2x+3;
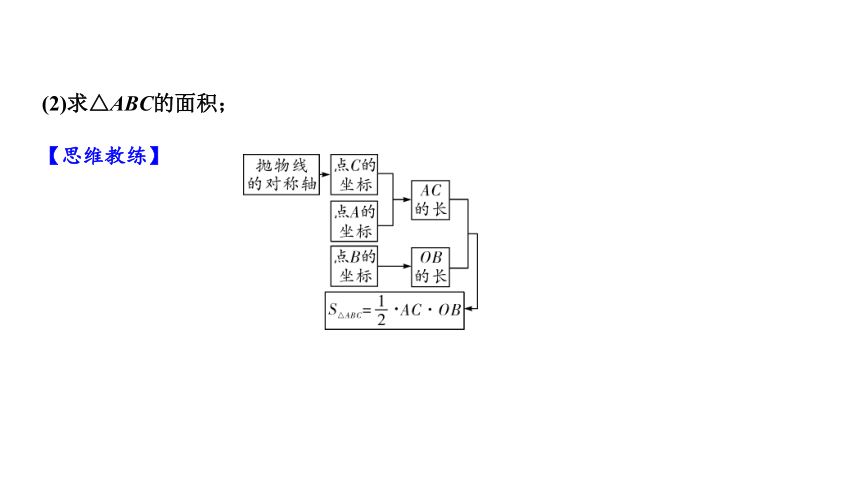
(2)求△ABC的面积;
【思维教练】
∵B(0,3),
∴OB=3.
∵抛物线解析式为y=-x2-2x+3,
∴抛物线对称轴为直线x=- =-1.
又∵A(-3,0)、C两点关于抛物线对称轴对称,
∴C(1,0),
∴AC=4,
∴S△ABC= ·AC·OB= ×4×3=6;
(3)已知点G是直线AB上方抛物线上一动点,若S△ACG=2,求点G的坐标;
例2题图②
【思维教练】观察图形可知△ACG的面积为 AC×|yG|,根据题意先假设抛物线上存在一点G,然后过点G作GG′⊥x轴于G′,设点G的横坐标为g,以AC为底,GG′为高即可得到S△ACG关于g的函数解析式,再令其函数值为2,求解即可.
(3)如解图①,过G作GG′⊥x轴于点G′,
设点G的坐标为(g,-g2-2g+3),
∵点G在x轴上方,
∴-g2-2g+3>0,且-3∴S△ACG= AC·GG′= ×4×(-g2-2g+3).
∵S△ACG=2,
∴ ×4×(-g2-2g+3)=2,
解得g1=-1+ (不合题意,舍去),g2=-1- .
∴G点坐标为(-1- ,1);
例2题解图①
(4) 在抛物线上是否存在一点M(异于点C),使得S△ABM=S△ABC?若存在,求出M的坐标;若不存在,请说明理由.
例2题图③
【思维教练】由于点M在抛物线上的位置不确定,需考虑M点的不同位置,结合图形分两种情况讨论:①点M在直线AB的上方,可先设出M点的横坐标并用其表示△ABM的面积,再列方程求解;②点M在直线AB的下方,可通过平移直线AB,使其经过点C,利用“同底等高的三角形面积相等”来求解.
存在.(ⅰ)如解图②,当点M在直线AB的上方时,过M作MM′⊥x轴交直线AB于点N,交x轴于点M′,连接AM,BM,
设点M的坐标为(m,-m2-2m+3),则N(m,m+3),
∴MN=-m2-2m+3-(m+3)=-m2-3m,
∴S△ABM=S△AMN+S△BMN
= MN·AO
= ×(-m2-3m)×3
=- m2- m,
根据题意S△ABM=S△ABC=6,
则- m2- m=6,即m2+3m+4=0,
此时方程无解,则不存在这样的M;
例2题解图②
(ⅱ)如解图③,当点M在直线AB的下方时,
∵S△ABM=S△ABC,
∴以AB作底,只要△ABM与△ABC的高相等即可.
故平移直线AB,使其过点C,此时平移后的直线与抛物线的交点即为M.
设平移后的直线CM的解析式为y=x+3+b,
将点C(1,0)代入得b=-4,
∴直线CM的解析式为y=x-1,
与抛物线联立得
解得 (舍去),
∴存在这样的点M,其坐标为(-4,-5);
例2题解图③
(5)已知点P是直线AB上方抛物线上的一动点,设点P的横坐标为p,求四边形AOBP面积的最大值.
例2题图④
【思维教练】要求四边形AOBP面积的最大值,观察可得不易采用面积公式直接求解,则此时需想到用“分割法”,将其面积分割为△ABP与△AOB的面积之和,△AOB的面积为定值,所以只需求△ABP面积的最大值,即可求得四边形AOBP面积的最大
∵S四边形AOBP=S△ABP+S△AOB,
S△AOB= AO·OB= ×3×3= ,
∴要求四边形AOBP的面积最大值,只需求△ABP面积的最大值.
∵点P在抛物线上,
∴点P的坐标为(p,-p2-2p+3),且-3<p<0.
如解图④,过P作PP′∥y轴交直线AB于点P′,则P′(p,p+3),
例2题解图④
∴PP′=-p2-2p+3-(p+3)=-p2-3p,
∴S△ABP=S△APP′+S△BPP′= PP′·AO= ×3(-p2-3p)=- p2- p=- (p+ )2+
∴当p=- 时,S△ABP有最大值,最大值为 ,
∴S四边形AOBP= + = ,
∴S四边形AOBP的最大值为 .
玩转贵阳10年中考真题
二次函数的综合应用(每年必考)
命题点
1
1. (2018贵阳15题4分)如图,在△ABC中,BC=6,BC边上的高为4,在△ABC的内部作一个矩形EFGH,使EF在BC边上,另外两个顶点分别在AB,AC边上,则对角线EG长的最小值为________.
第1题图
2. (2011贵阳21题10分)如图所示,二次函数y=-x2+2x+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C.
(1)求m的值;
(2)求点B的坐标;
(3)该二次函数图象上有一点D(x,y)(其中x>0,y>0)使S△ABD=S△ABC,求点D的坐标.
第2题图
解:(1)把A(3,0)代入y=-x2+2x+m,得-9+6+m=0,
∴m=3;(3分)
(2)由(1)得y=-x2+2x+3,令y=0得-x2+2x+3=0.
解得x1=-1,x2=3,
∴点B的坐标为(-1,0);(6分)
(3)设点D的坐标为(x,y),
∵x>0,y>0,要使S△ABD=S△ABC,则点D的纵坐标与点C的纵坐标必相等.
∴y=3,即-x2+2x+3=3.(8分)
解得x1=0,x2=2,
∴点D的坐标为(2,3).(10分)
3. (2016贵阳25题12分)如图,直线y=5x+5交x轴于点A,交y轴于点C,过A,C两点的二次函数y=ax2+4x+c的图象交x轴于另一点B.
(1)求二次函数的表达式;
(2)连接BC,点N是线段BC上的动点,作ND⊥x轴交二次函数的图象于点D,求线段ND长度的最大值;
(3)若点H为二次函数y=ax2+4x+c图象的顶点,点M(4,m)是该二次函数图象上一点,在x轴,y轴上分别找点F,E,使四边形HEFM的周长最小,求出点F,E的坐标.
第3题图
温馨提示:在直角坐标系中,若点P,Q的坐标分别为P(x1,y1),Q(x2,y2),当PQ平行x轴时,线段PQ的长度可由公式PQ=|x1-x2|求出;当PQ平行y轴时,线段PQ的长度可由公式PQ=|y1-y2|求出.
解:(1)∵直线y=5x+5与x轴交于点A,与y轴交于点C,
∴A(-1,0),C(0,5).
∵抛物线y=ax2+4x+c过点A(-1,0),C(0,5),
∴
解得
∴二次函数的表达式为y=-x2+4x+5;(4分)
(2)∵抛物线y=-x2+4x+5与x轴交于A,B两点,
∴解得-x2+4x+5=0的两根为x1=-1,x2=5.
∵点B在x轴正半轴,∴B(5,0).
设过B(5,0), C(0,5)的直线BC表达式为y=kx+b,则
解得k=-1,b=5,
∴直线BC表达式为y=-x+5.
∵DN⊥x轴,∴DN∥y轴.
∵点N在BC上,点D在抛物线上,设N(x,y1),D(x,y2),
∴N(x,-x+5),D(x,-x2+4x+5).
∴DN=-x2+4x+5+x-5=-x2+5x=-(x- )2+ .
当x= 时,DN有最大值 ;(8分)
(3)由题意可得二次函数的顶点坐标为H(2,9),点M的坐标为M(4,5),
如解图,作点H(2,9)关于y轴的对称点H1,则点H1的坐标为(-2,9),
作点M(4,5)关于x轴的对称点M1,则点M1的坐标为M1(4,-5),
连接H1M1分别交x轴于点F,y轴于点E,
∴H1M1+HM的长度是四边形HEFM的最小周长,则点F,E即为所求,
设直线H1M1的函数表达式为y=k1x+b1,
直线H1M1过点M1(4,-5),H1(-2,9),
根据题意得
解得 ,∴y=- x+ ,
∴点F,E的坐标分别为F( ,0),E(0, ).(12分)
第3题解图
二次函数的实际应用(10年3考)
命题点
2
4. (2018贵阳22题10分)六盘水市梅花山国际滑雪场自建成以来,吸引了大批滑雪爱好者,一滑雪者从山坡滑下,测得滑行距离y(单位:m)与滑行时间x(单位:s)之间的关系可以近似地用二次函数来表示,现测得一组数据,如下表所示.
滑行时间x/s
0
1
2
3
…
滑行距离y/m
0
4
12
24
…
(1)根据表中数据求出二次函数的表达式,现测量出滑雪者的出发点与终点的距离大约840米,他需要多少时间才能到达终点?
(2)将得到的二次函数图象补充完整后,向左平移2个单位,再向下平移5个单位,求平移后所得函数的表达式.
(1)设二次函数表达式为:y=ax2+bx+c,则 解得
∴二次函数的表达式为y=2x2+2x(x≥0),(4分)
∴当y=840时,即2x2+2x=840,
解得x=20或x=-21(舍去),
∴他需要20s才能到达终点;(6分)
(2)补全图象如解图,
∵y=2x2+2x=2(x+ )2- ,
∴向左平移2个单位,再向下平移5个单位后函数表达式为y=2(x+ +2)2- -5=2(x+ )2- .(10分)
第4题解图
5. (2010贵阳23题12分)某商场以每件50元的价格购进一种商品,销售中发现这种商品每天的销售数量m(件)与每件的销售价格x(元)满足一次函数,其图象如图所示.
(1)每天的销售数量m(件)与每件的销售价格x(元)的函数表达式是___________________________;
(2)求该商场每天销售这种商品的销售利润y(元)与每件的
销售价格x(元)之间的函数表达式;
(3)每件商品的销售价格在什么范围内,每天的销售利润随着销售价格的提高而增加?
第5题图
m=-x+100(0≤x≤100)
【解法提示】设一次函数的一般表达式为m=kx+b,将(0,100)、(100,0)代入得:
即m=-x+100(0≤x≤100).
(2)每件商品的利润为(x-50)元,∴每天的销售利润为:
y=(x-50)(-x+100),
∴函数表达式为y=-x2+150x-5000=-(x-75)2+625;(7分)
(3)∵对称轴为直线x=75,且抛物线开口向下,
∴在50<x≤75元时,每天的销售利润随着销售价格的提高而增加.(12分)
6. (2011贵阳25题12分)用长度一定的不锈钢材料设计成外观为矩形的框架(如图①②③中的一种).
设竖档AB=x米,请根据以上图案回答下列问题:(题中的不锈钢材料总长度均指各图中所有黑线的长度和,所有横档和竖档分别与AD、AB平行)
(1)在图①中,如果不锈钢材料总长度为12米,当x为多少时,矩形框架ABCD的面积为3平方米?
第6题图
(2)在图②中,如果不锈钢材料总长度为12米,当x为多少时,矩形框架ABCD的面积S最大?最大面积是多少?
(3)在图③中,如果不锈钢材料总长度为a米,共有n条竖档,那么当x为多少时,矩形框架ABCD的面积S最大?最大面积是多少?
解:(1)由题意知:BC的长为 =(4-x)米.(1分)
依题意得x(4-x)=3,即x2-4x+3=0.
解得x1=1,x2=3.(3分)
即当AB的长度为1米或3米时,矩形框架ABCD的面积为3平方米;(4分)
(2)由题意知,BC长为 =(4- x)米,
∴S=x(4- x)=- x2+4x=- (x- )2+3;(6分)
∵- <0,
∴当x= 时,S有最大值3.(7分)
即当x为 米时,矩形框架ABCD的面积S最大,最大面积是3平方米;(8分)
(3)由题意知,BC长为 米,
∴S=x×( )=- x2+ x=- (x- )2+ .(11分)
因此,当x为 米时,矩形框架ABCD的面积S最大,最大面积是 平方米.(12分)
(必考,1~2道,解答题必考1道)
类型一 与线段有关的问题
重难点突破
例 1 如图,抛物线y=- x2+bx+c与直线y= x-2交于点A、C.
(1)求抛物线的解析式;
例1题图①
【思维教练】
解:∵直线y= x-2经过点A、C,
∴点A(4,0),点C(0,-2).
将点A(4,0),点C(0,-2),代入抛物线y=- x2+bx+c中,
得
解得
∴抛物线的解析式为y=- x2+ x-2;
(2)设点E为x轴上一点,当AE=CE时,求点E的坐标;
【思维教练】设出点E的坐标,表示出AE的长,CE的长可利用勾股定理表示,联立方程即可求出点E的坐标.
如解图①,由点E在x轴上,可设点E的坐标为(e,0),连接CE,则AE=4-e.
在Rt△COE中,根据勾股定理得CE2=OC2+OE2=(-2)2+e2=22+e2,
∵AE=CE,
∴(4-e)2=22+e2,解得e= ,则点E的坐标为( ,0);
例1题解图①
(3)设点P为位于直线AC上方抛物线上一动点,过点P作y轴的平行线交直线AC于点H,①求当PH值最大时,点P的坐标;②过点P作PD⊥AC,求PD的最大值;
例1题图②
【思维教练】①
②要求PD的最大值,不能直接用P,D坐标表示PD的长,可通过PH的长和锐角函数值来表示PD的长,通过二次函数的性质即可求得最值.
①设点P(x,- x2+ x-2),则H(x, x-2),
∴PH=- x2+ x-2- x+2
=- x2+2x=- (x-2)2+2,且0<x<4,
∴当x=2时,PH值最大,最大值为2,
∴当PH值最大时,点P为(2,1);
②如解图②,由①知,PH=- (x-2)2+2,且0<x<4,
∴PD=PH·sin∠PHD=PH·sin∠OCA= PH=- (x-2)2+ ,
∴当x=2时,PD有最大值 ;
例1题解图②
(4)在抛物线对称轴l上是否存在一点F,使得△BCF的周长最小,若存在,求出点F的坐标及△BCF周长的最小值;若不存在,请说明理由.
【思维教练】因为BC长为定值,要使△BCF周长最小,即要使CF+BF的值最小,由点A、B关于对称轴l对称,可知AC与对称轴l的交点即为点F,即可使CF+BF最小.
存在.要使△BCF的周长最小,即BC+BF+CF最小,如解图③所示.
在Rt△OBC中,OB=1,OC=2,由勾股定理得BC=
= 为定值,∴当BF+CF最小时,C△BCF最小.
∵点B与点A关于直线l对称,
∴AC与对称轴l的交点即为所求的点F,
易得抛物线y=- x2+ x-2的对称轴为直线x= ,将x= 代入y= x-2,得y= × -2=- ,
∴点F的坐标为( ,- ).
在Rt△AOC中,由AO=4,OC=2,根据勾股定理得AC= =2 ,
∴△BCF周长的最小值为BC+BF+CF=BC+AC= +2 =3 .
例1题解图③
类型二 与面积有关的问题
例 2 如图,已知抛物线y=-x2+bx+c与直线AB相交于A(-3,0),B(0,3)两点,与x轴的另一个交点为C.抛物线对称轴为直线l,顶点为D,对称轴与x轴的交点为E,连接BC.
(1)求直线AB的解析式及抛物线的解析式;
例2题图①
【思维教练】
解:(1)设直线AB的解析式为y=kx+d(k≠0),
将A(-3,0),B(0,3)代入,
得 解得
∴直线AB的解析式为y=x+3.
将A(-3,0),B(0,3)代入抛物线解析式y=-x2+bx+c中,
得
解得
∴抛物线的解析式为y=-x2-2x+3;
(2)求△ABC的面积;
【思维教练】
∵B(0,3),
∴OB=3.
∵抛物线解析式为y=-x2-2x+3,
∴抛物线对称轴为直线x=- =-1.
又∵A(-3,0)、C两点关于抛物线对称轴对称,
∴C(1,0),
∴AC=4,
∴S△ABC= ·AC·OB= ×4×3=6;
(3)已知点G是直线AB上方抛物线上一动点,若S△ACG=2,求点G的坐标;
例2题图②
【思维教练】观察图形可知△ACG的面积为 AC×|yG|,根据题意先假设抛物线上存在一点G,然后过点G作GG′⊥x轴于G′,设点G的横坐标为g,以AC为底,GG′为高即可得到S△ACG关于g的函数解析式,再令其函数值为2,求解即可.
(3)如解图①,过G作GG′⊥x轴于点G′,
设点G的坐标为(g,-g2-2g+3),
∵点G在x轴上方,
∴-g2-2g+3>0,且-3
∵S△ACG=2,
∴ ×4×(-g2-2g+3)=2,
解得g1=-1+ (不合题意,舍去),g2=-1- .
∴G点坐标为(-1- ,1);
例2题解图①
(4) 在抛物线上是否存在一点M(异于点C),使得S△ABM=S△ABC?若存在,求出M的坐标;若不存在,请说明理由.
例2题图③
【思维教练】由于点M在抛物线上的位置不确定,需考虑M点的不同位置,结合图形分两种情况讨论:①点M在直线AB的上方,可先设出M点的横坐标并用其表示△ABM的面积,再列方程求解;②点M在直线AB的下方,可通过平移直线AB,使其经过点C,利用“同底等高的三角形面积相等”来求解.
存在.(ⅰ)如解图②,当点M在直线AB的上方时,过M作MM′⊥x轴交直线AB于点N,交x轴于点M′,连接AM,BM,
设点M的坐标为(m,-m2-2m+3),则N(m,m+3),
∴MN=-m2-2m+3-(m+3)=-m2-3m,
∴S△ABM=S△AMN+S△BMN
= MN·AO
= ×(-m2-3m)×3
=- m2- m,
根据题意S△ABM=S△ABC=6,
则- m2- m=6,即m2+3m+4=0,
此时方程无解,则不存在这样的M;
例2题解图②
(ⅱ)如解图③,当点M在直线AB的下方时,
∵S△ABM=S△ABC,
∴以AB作底,只要△ABM与△ABC的高相等即可.
故平移直线AB,使其过点C,此时平移后的直线与抛物线的交点即为M.
设平移后的直线CM的解析式为y=x+3+b,
将点C(1,0)代入得b=-4,
∴直线CM的解析式为y=x-1,
与抛物线联立得
解得 (舍去),
∴存在这样的点M,其坐标为(-4,-5);
例2题解图③
(5)已知点P是直线AB上方抛物线上的一动点,设点P的横坐标为p,求四边形AOBP面积的最大值.
例2题图④
【思维教练】要求四边形AOBP面积的最大值,观察可得不易采用面积公式直接求解,则此时需想到用“分割法”,将其面积分割为△ABP与△AOB的面积之和,△AOB的面积为定值,所以只需求△ABP面积的最大值,即可求得四边形AOBP面积的最大
∵S四边形AOBP=S△ABP+S△AOB,
S△AOB= AO·OB= ×3×3= ,
∴要求四边形AOBP的面积最大值,只需求△ABP面积的最大值.
∵点P在抛物线上,
∴点P的坐标为(p,-p2-2p+3),且-3<p<0.
如解图④,过P作PP′∥y轴交直线AB于点P′,则P′(p,p+3),
例2题解图④
∴PP′=-p2-2p+3-(p+3)=-p2-3p,
∴S△ABP=S△APP′+S△BPP′= PP′·AO= ×3(-p2-3p)=- p2- p=- (p+ )2+
∴当p=- 时,S△ABP有最大值,最大值为 ,
∴S四边形AOBP= + = ,
∴S四边形AOBP的最大值为 .
玩转贵阳10年中考真题
二次函数的综合应用(每年必考)
命题点
1
1. (2018贵阳15题4分)如图,在△ABC中,BC=6,BC边上的高为4,在△ABC的内部作一个矩形EFGH,使EF在BC边上,另外两个顶点分别在AB,AC边上,则对角线EG长的最小值为________.
第1题图
2. (2011贵阳21题10分)如图所示,二次函数y=-x2+2x+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C.
(1)求m的值;
(2)求点B的坐标;
(3)该二次函数图象上有一点D(x,y)(其中x>0,y>0)使S△ABD=S△ABC,求点D的坐标.
第2题图
解:(1)把A(3,0)代入y=-x2+2x+m,得-9+6+m=0,
∴m=3;(3分)
(2)由(1)得y=-x2+2x+3,令y=0得-x2+2x+3=0.
解得x1=-1,x2=3,
∴点B的坐标为(-1,0);(6分)
(3)设点D的坐标为(x,y),
∵x>0,y>0,要使S△ABD=S△ABC,则点D的纵坐标与点C的纵坐标必相等.
∴y=3,即-x2+2x+3=3.(8分)
解得x1=0,x2=2,
∴点D的坐标为(2,3).(10分)
3. (2016贵阳25题12分)如图,直线y=5x+5交x轴于点A,交y轴于点C,过A,C两点的二次函数y=ax2+4x+c的图象交x轴于另一点B.
(1)求二次函数的表达式;
(2)连接BC,点N是线段BC上的动点,作ND⊥x轴交二次函数的图象于点D,求线段ND长度的最大值;
(3)若点H为二次函数y=ax2+4x+c图象的顶点,点M(4,m)是该二次函数图象上一点,在x轴,y轴上分别找点F,E,使四边形HEFM的周长最小,求出点F,E的坐标.
第3题图
温馨提示:在直角坐标系中,若点P,Q的坐标分别为P(x1,y1),Q(x2,y2),当PQ平行x轴时,线段PQ的长度可由公式PQ=|x1-x2|求出;当PQ平行y轴时,线段PQ的长度可由公式PQ=|y1-y2|求出.
解:(1)∵直线y=5x+5与x轴交于点A,与y轴交于点C,
∴A(-1,0),C(0,5).
∵抛物线y=ax2+4x+c过点A(-1,0),C(0,5),
∴
解得
∴二次函数的表达式为y=-x2+4x+5;(4分)
(2)∵抛物线y=-x2+4x+5与x轴交于A,B两点,
∴解得-x2+4x+5=0的两根为x1=-1,x2=5.
∵点B在x轴正半轴,∴B(5,0).
设过B(5,0), C(0,5)的直线BC表达式为y=kx+b,则
解得k=-1,b=5,
∴直线BC表达式为y=-x+5.
∵DN⊥x轴,∴DN∥y轴.
∵点N在BC上,点D在抛物线上,设N(x,y1),D(x,y2),
∴N(x,-x+5),D(x,-x2+4x+5).
∴DN=-x2+4x+5+x-5=-x2+5x=-(x- )2+ .
当x= 时,DN有最大值 ;(8分)
(3)由题意可得二次函数的顶点坐标为H(2,9),点M的坐标为M(4,5),
如解图,作点H(2,9)关于y轴的对称点H1,则点H1的坐标为(-2,9),
作点M(4,5)关于x轴的对称点M1,则点M1的坐标为M1(4,-5),
连接H1M1分别交x轴于点F,y轴于点E,
∴H1M1+HM的长度是四边形HEFM的最小周长,则点F,E即为所求,
设直线H1M1的函数表达式为y=k1x+b1,
直线H1M1过点M1(4,-5),H1(-2,9),
根据题意得
解得 ,∴y=- x+ ,
∴点F,E的坐标分别为F( ,0),E(0, ).(12分)
第3题解图
二次函数的实际应用(10年3考)
命题点
2
4. (2018贵阳22题10分)六盘水市梅花山国际滑雪场自建成以来,吸引了大批滑雪爱好者,一滑雪者从山坡滑下,测得滑行距离y(单位:m)与滑行时间x(单位:s)之间的关系可以近似地用二次函数来表示,现测得一组数据,如下表所示.
滑行时间x/s
0
1
2
3
…
滑行距离y/m
0
4
12
24
…
(1)根据表中数据求出二次函数的表达式,现测量出滑雪者的出发点与终点的距离大约840米,他需要多少时间才能到达终点?
(2)将得到的二次函数图象补充完整后,向左平移2个单位,再向下平移5个单位,求平移后所得函数的表达式.
(1)设二次函数表达式为:y=ax2+bx+c,则 解得
∴二次函数的表达式为y=2x2+2x(x≥0),(4分)
∴当y=840时,即2x2+2x=840,
解得x=20或x=-21(舍去),
∴他需要20s才能到达终点;(6分)
(2)补全图象如解图,
∵y=2x2+2x=2(x+ )2- ,
∴向左平移2个单位,再向下平移5个单位后函数表达式为y=2(x+ +2)2- -5=2(x+ )2- .(10分)
第4题解图
5. (2010贵阳23题12分)某商场以每件50元的价格购进一种商品,销售中发现这种商品每天的销售数量m(件)与每件的销售价格x(元)满足一次函数,其图象如图所示.
(1)每天的销售数量m(件)与每件的销售价格x(元)的函数表达式是___________________________;
(2)求该商场每天销售这种商品的销售利润y(元)与每件的
销售价格x(元)之间的函数表达式;
(3)每件商品的销售价格在什么范围内,每天的销售利润随着销售价格的提高而增加?
第5题图
m=-x+100(0≤x≤100)
【解法提示】设一次函数的一般表达式为m=kx+b,将(0,100)、(100,0)代入得:
即m=-x+100(0≤x≤100).
(2)每件商品的利润为(x-50)元,∴每天的销售利润为:
y=(x-50)(-x+100),
∴函数表达式为y=-x2+150x-5000=-(x-75)2+625;(7分)
(3)∵对称轴为直线x=75,且抛物线开口向下,
∴在50<x≤75元时,每天的销售利润随着销售价格的提高而增加.(12分)
6. (2011贵阳25题12分)用长度一定的不锈钢材料设计成外观为矩形的框架(如图①②③中的一种).
设竖档AB=x米,请根据以上图案回答下列问题:(题中的不锈钢材料总长度均指各图中所有黑线的长度和,所有横档和竖档分别与AD、AB平行)
(1)在图①中,如果不锈钢材料总长度为12米,当x为多少时,矩形框架ABCD的面积为3平方米?
第6题图
(2)在图②中,如果不锈钢材料总长度为12米,当x为多少时,矩形框架ABCD的面积S最大?最大面积是多少?
(3)在图③中,如果不锈钢材料总长度为a米,共有n条竖档,那么当x为多少时,矩形框架ABCD的面积S最大?最大面积是多少?
解:(1)由题意知:BC的长为 =(4-x)米.(1分)
依题意得x(4-x)=3,即x2-4x+3=0.
解得x1=1,x2=3.(3分)
即当AB的长度为1米或3米时,矩形框架ABCD的面积为3平方米;(4分)
(2)由题意知,BC长为 =(4- x)米,
∴S=x(4- x)=- x2+4x=- (x- )2+3;(6分)
∵- <0,
∴当x= 时,S有最大值3.(7分)
即当x为 米时,矩形框架ABCD的面积S最大,最大面积是3平方米;(8分)
(3)由题意知,BC长为 米,
∴S=x×( )=- x2+ x=- (x- )2+ .(11分)
因此,当x为 米时,矩形框架ABCD的面积S最大,最大面积是 平方米.(12分)
