北师大版九年级数学下册课件3.6直线和圆的位置关系 课件(共28张PPT)
文档属性
| 名称 | 北师大版九年级数学下册课件3.6直线和圆的位置关系 课件(共28张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-17 09:07:19 | ||
图片预览





文档简介
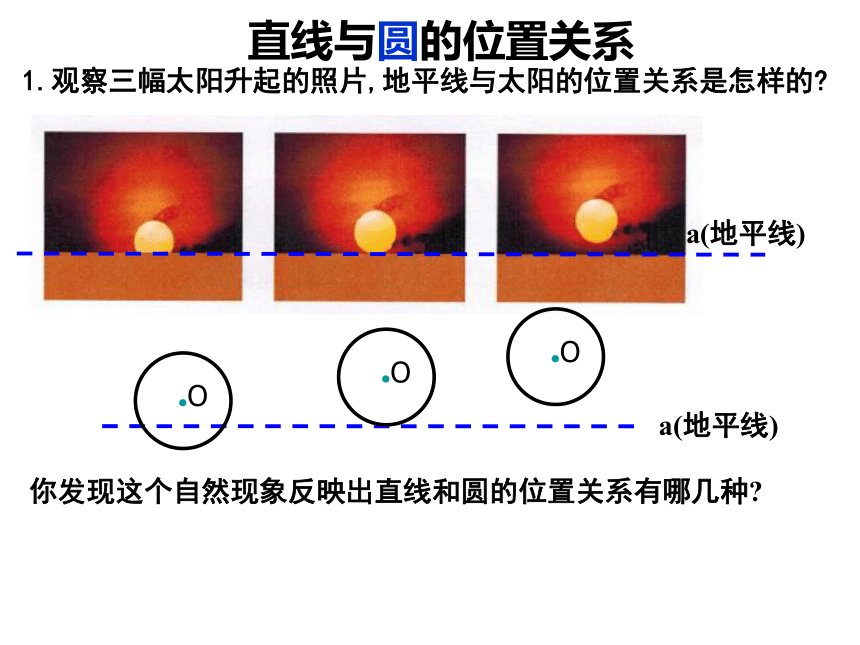
6 直线和圆的位置关系
九年级数学(下)第三章 圆
●O
●O
●O
4.确定圆的条件——
不在同一直线上的三点
圆心、半径
3.定理
不在同一条直线上的三个点确定一个圆.
1.经过一点可以作无数条直线;
2. 经过两个已知点A、B能作无数个圆
知识回顾
5.锐角三角形 在三角形的内部
直角三角形 --外心的位置--- 在斜边中点上
钝角三角形 在三角形的外部
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
知识回顾
6.点与圆的位置关系:
设⊙O的半径为r,则点P与⊙O的位置关系有:
(1)点P在⊙O上 OP=r
(2)点P在⊙O内 OP<r
(3)点P在⊙O外 OP>r
知识回顾
●O
●P1
●P2
●P3
直线与圆的位置关系
1.观察三幅太阳升起的照片,地平线与太阳的位置关系是怎样的?
你发现这个自然现象反映出直线和圆的位置关系有哪几种?
a(地平线)
a(地平线)
●O
●O
●O
直线与圆的位置关系
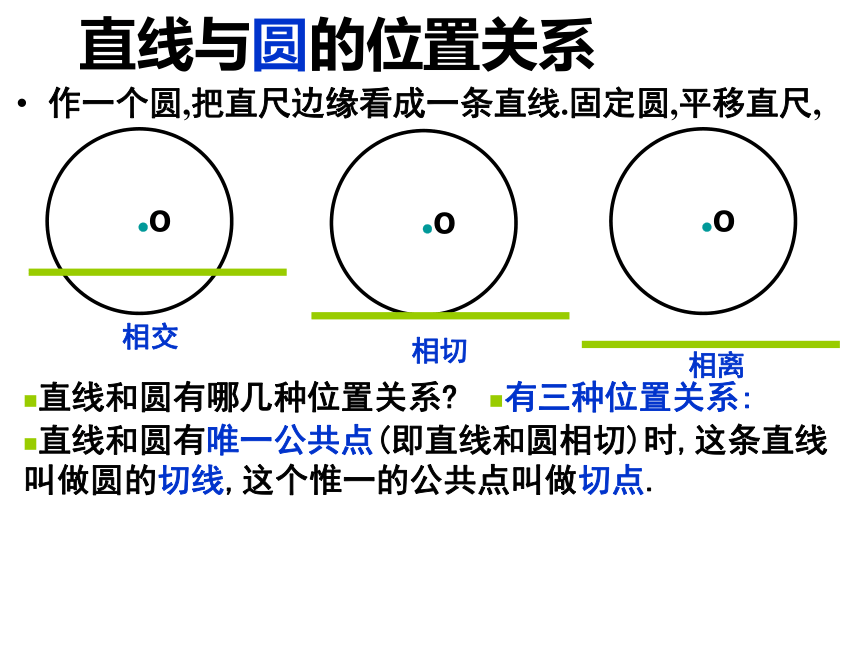
作一个圆,把直尺边缘看成一条直线.固定圆,平移直尺,
直线和圆有哪几种位置关系?
●O
●O
有三种位置关系:
相交
直线和圆有唯一公共点(即直线和圆相切)时,这条直线叫做圆的切线,这个惟一的公共点叫做切点.
●O
相离
相切
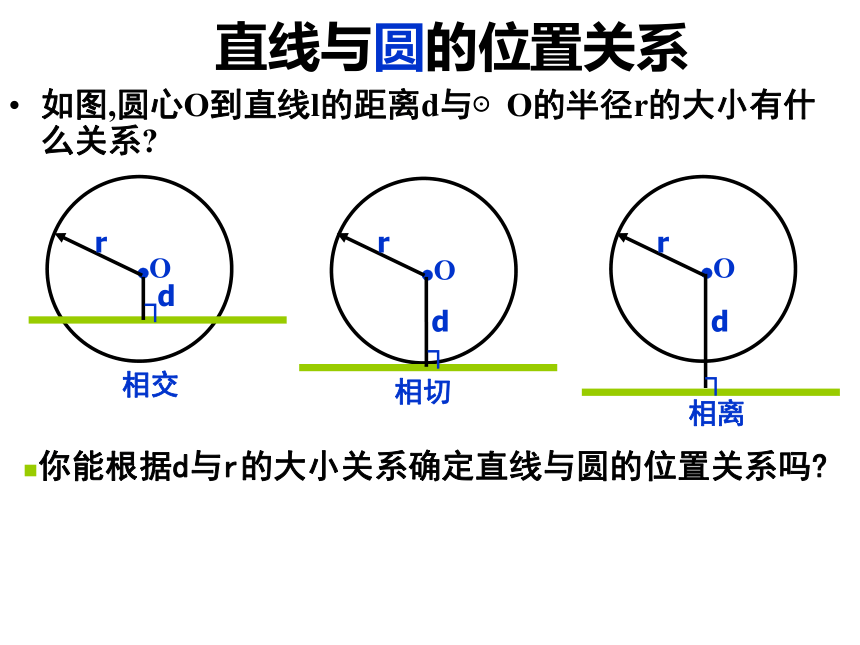
如图,圆心O到直线l的距离d与⊙O的半径r的大小有什么关系?
你能根据d与r的大小关系确定直线与圆的位置关系吗?
●O
●O
相交
●O
相切
相离
直线与圆的位置关系
r
r
r
d
┐
d
┐
┐
d
直线和圆相交
d r;
d r;
直线和圆相切
直线和圆相离
d r;
直线与圆的位置关系
<
=
>
●O
●O
相交
●O
相切
相离
r
r
r
d
┐
d
┐
┐
d
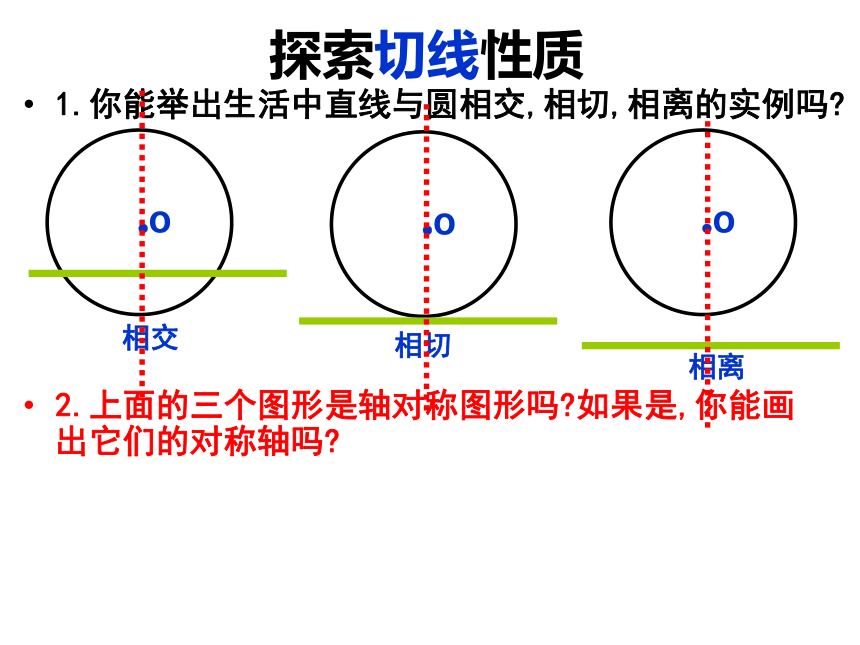
探索切线性质
1.你能举出生活中直线与圆相交,相切,相离的实例吗?
2.上面的三个图形是轴对称图形吗?如果是,你能画出它们的对称轴吗?
●O
●O
相交
●O
相切
相离
探索切线性质
如图,直线CD与⊙O相切于点A,直径AB与直线CD有怎样的位置关系?说说你的理由.
直径AB垂直于直线CD.
小颖的理由是:
∵右图是轴对称图形,AB是对称轴,
∴沿直线AB对折图形时,AC与AD重合,因此,∠BAC=∠BAD=90°.
C
D
B
●O
A
探索切线性质
小亮的理由是:直径AB与直线CD要么垂直,要么不垂直.
假设AB与CD不垂直,过点O作一条直径垂直于CD,垂足为M,
则OMC
D
B
●O
A
所以AB与CD垂直.
M
切线的性质定理
参考小颖和小亮的说理过程,请你写出这个命题
定理 圆的切线垂直于过切点的半径.
老师提示:
切线的性质定理是证明两线垂直的重要根据;
作过切点的半径是常用经验辅助线之一.
如图
∵CD是⊙O的切线,A是切点,OA是⊙O的半径,
∴CD⊥OA.
C
D
B
●O
A
直线何时变为切线
如图,AB是⊙O的直径,直线CD经过点A,CD与AB的夹角为∠α,当CD绕点A旋转时,
你能写出一个命题来表述这个事实吗?
1.随着∠α的变化,点O到CD的距离如何变化?直线CD与⊙O的位置关系如何变化?
2.当∠α等于多少度时,点O到CD的距离等于半径?此时,直线CD与⊙O有的位置关系?有为什么?
B
●O
A
C
D
┓
d
α
┏
d
α
d
┓
切线的判定定理
定理 过半径的外端,并且垂直于这条半径的直线是圆的切线.
C
D
B
●O
A
如图
∵OA是⊙O的半径,直线CD经过A点,且CD⊥OA,
∴ CD是⊙O的切线.
判定定理2:到圆心的距离等于半径的直线是圆的切线
判定定理1:经过半径外端点且垂直于这条半径的直线是圆的切线
切线的判定
例 如图,在△ABC中,作一个圆使它与这个三角形三边都相切.
老师提示:
假设符合条件的圆已作出,则它的圆心到三边的距离相等.因此,圆心在这个三角形三个角的平分线上,半径为圆心到三边的距离.
A
B
C
A
B
C
┓
┗
┗
┓
I●
●
●
●
●
┓
┗
┗
┓
┗
┗
┓
┗
┗
I●
┓
●
例 如图,在△ABC中,作一个圆使它与这个三角形三边都相切.
解:1.作∠B、∠C的平分线BE和CF,交点为I;
2.过I作ID⊥BC,垂足为D;
3.以I为圆,以ID为半径作⊙I.
∴ ⊙I就是所求的圆.
A
B
C
I●
┓
●
E
F
D
这样的圆可以作出几个?为什么?.
∵直线BE和CF只有一个交点I,并且点I到 △ABC三边的距离相等(为什么?),
∴因此和△ABC三边都相切的圆可以作出一个,并且只能作一个.
三角形与圆的位置关系
A
B
C
I●
●
┓
┗
┗
E
F
D
三角形与圆的位置关系
和三角形三边都相切的圆叫做三角形的内切圆.这个三角形叫做圆的外切三角形.
内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心.
老师提示:
多边形的边与圆的位置关系称为切.
A
B
C
●
I
A
B
C
I●
●
┓
┗
┗
E
F
D
内心到三角形三边的距离相等.
切线的性质定理的应用
1.已知Rt△ABC的斜边AB=8cm,直角边AC=4cm.
(1)以点C为圆心作圆,当半径为多长时,AB与⊙C 相切?
A
C
B
┐
解:(1)过C作CD⊥AB,垂足为D.
D
┛
∵AB=8cm,AC=4cm.
∴∠A=60°.
因此,当半径长为 cm时,AB与⊙C相切.
∴∠B=30°.
切线的性质定理的应用
1.已知Rt△ABC的斜边AB=8cm,直角边AC=4cm.
(2)以点C为圆心,分别以2cm,4cm为半径作两个圆,这两个圆与AB分别有怎样的位置关系?
当r=4cm时,dA
C
B
┐
D
┛
当r=2cm时,d>r,AB与⊙C相离;
解:(2)由(1)可知,圆心到AB的距离d= cm,所以
1.在Rt△ABC中, ∠C= 90°, ∠B= 30°,O为AB上一点, OA=m,⊙O的半径为r。当r与m满足怎样的关系时,
1)AC与⊙O相交?
2)AC与⊙O相切?
3)AC与⊙O相离?
知识技能
C
B
A
O
m
r
1.在Rt△ABC中, ∠C= 90°, ∠B= 30°,O为AB上一点, OA=m,⊙O的半径为r。当r与m满足怎样的关系时,
1)AC与⊙O相交?
2)AC与⊙O相切?
3)AC与⊙O相离?
D
练一练
2. 判断题
3.以三角形的一边为直径的圆恰好与另一边相切,则此三角形是__________三角形
直角
(1) 垂直于圆的半径的直线一定是这个圆的切线.( )
(2) 过圆的半径的外端的直线一定是这个圆的切线 . ( )
×
×
这节课有何收获?!
作业
1.用如下方法可以估测河流的大致宽度:如图,观测者站在岸边O处投下 一块石头,激起的半圆形波纹逐渐向远处扩展,当波纹刚好抵达对岸时,另一观测者记录下波纹沿着观测者所在岸边所扩展的距离,这一距离就是河流的大致宽度,请说明这种方法的合理性。
2. 以边长为3,4,5的三角形的三个顶点为圆心,分别作圆与对边相切,则这三个圆的半径分别是多少?
C
A
B
┐
数学理解
3.为了测量一个光盘的的直径,小明把直尺、光盘和三角尺按图所示放置于桌面上,并量出AB=6cm。这张光盘的直径是多少?
3.为了测量一个光盘的的直径,小明把直尺、光盘和三角尺按图所示放置于桌面上,并量出AB=6cm。这张光盘的直径是多少?
O
C
2
1
3
补充定理
已知:如图,P是⊙O外一点,PA是⊙O的切线,AB是弦.
A
B
P
●O
PA2=PB·PC
C
∠PAB= ∠C
弦切角:
弦与切线的夹角(∠PAB)
弦切角等于它所夹的弧所对的圆周角。
(∠PAB = C= ∠D)
D
1
2
3
如图,圆O中弦AB与CD相交于P,你有什么新发现吗?
·O
D
P
A
C
B
PA·PB=PC·PD
练习
九年级数学(下)第三章 圆
●O
●O
●O
4.确定圆的条件——
不在同一直线上的三点
圆心、半径
3.定理
不在同一条直线上的三个点确定一个圆.
1.经过一点可以作无数条直线;
2. 经过两个已知点A、B能作无数个圆
知识回顾
5.锐角三角形 在三角形的内部
直角三角形 --外心的位置--- 在斜边中点上
钝角三角形 在三角形的外部
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
知识回顾
6.点与圆的位置关系:
设⊙O的半径为r,则点P与⊙O的位置关系有:
(1)点P在⊙O上 OP=r
(2)点P在⊙O内 OP<r
(3)点P在⊙O外 OP>r
知识回顾
●O
●P1
●P2
●P3
直线与圆的位置关系
1.观察三幅太阳升起的照片,地平线与太阳的位置关系是怎样的?
你发现这个自然现象反映出直线和圆的位置关系有哪几种?
a(地平线)
a(地平线)
●O
●O
●O
直线与圆的位置关系
作一个圆,把直尺边缘看成一条直线.固定圆,平移直尺,
直线和圆有哪几种位置关系?
●O
●O
有三种位置关系:
相交
直线和圆有唯一公共点(即直线和圆相切)时,这条直线叫做圆的切线,这个惟一的公共点叫做切点.
●O
相离
相切
如图,圆心O到直线l的距离d与⊙O的半径r的大小有什么关系?
你能根据d与r的大小关系确定直线与圆的位置关系吗?
●O
●O
相交
●O
相切
相离
直线与圆的位置关系
r
r
r
d
┐
d
┐
┐
d
直线和圆相交
d r;
d r;
直线和圆相切
直线和圆相离
d r;
直线与圆的位置关系
<
=
>
●O
●O
相交
●O
相切
相离
r
r
r
d
┐
d
┐
┐
d
探索切线性质
1.你能举出生活中直线与圆相交,相切,相离的实例吗?
2.上面的三个图形是轴对称图形吗?如果是,你能画出它们的对称轴吗?
●O
●O
相交
●O
相切
相离
探索切线性质
如图,直线CD与⊙O相切于点A,直径AB与直线CD有怎样的位置关系?说说你的理由.
直径AB垂直于直线CD.
小颖的理由是:
∵右图是轴对称图形,AB是对称轴,
∴沿直线AB对折图形时,AC与AD重合,因此,∠BAC=∠BAD=90°.
C
D
B
●O
A
探索切线性质
小亮的理由是:直径AB与直线CD要么垂直,要么不垂直.
假设AB与CD不垂直,过点O作一条直径垂直于CD,垂足为M,
则OM
D
B
●O
A
所以AB与CD垂直.
M
切线的性质定理
参考小颖和小亮的说理过程,请你写出这个命题
定理 圆的切线垂直于过切点的半径.
老师提示:
切线的性质定理是证明两线垂直的重要根据;
作过切点的半径是常用经验辅助线之一.
如图
∵CD是⊙O的切线,A是切点,OA是⊙O的半径,
∴CD⊥OA.
C
D
B
●O
A
直线何时变为切线
如图,AB是⊙O的直径,直线CD经过点A,CD与AB的夹角为∠α,当CD绕点A旋转时,
你能写出一个命题来表述这个事实吗?
1.随着∠α的变化,点O到CD的距离如何变化?直线CD与⊙O的位置关系如何变化?
2.当∠α等于多少度时,点O到CD的距离等于半径?此时,直线CD与⊙O有的位置关系?有为什么?
B
●O
A
C
D
┓
d
α
┏
d
α
d
┓
切线的判定定理
定理 过半径的外端,并且垂直于这条半径的直线是圆的切线.
C
D
B
●O
A
如图
∵OA是⊙O的半径,直线CD经过A点,且CD⊥OA,
∴ CD是⊙O的切线.
判定定理2:到圆心的距离等于半径的直线是圆的切线
判定定理1:经过半径外端点且垂直于这条半径的直线是圆的切线
切线的判定
例 如图,在△ABC中,作一个圆使它与这个三角形三边都相切.
老师提示:
假设符合条件的圆已作出,则它的圆心到三边的距离相等.因此,圆心在这个三角形三个角的平分线上,半径为圆心到三边的距离.
A
B
C
A
B
C
┓
┗
┗
┓
I●
●
●
●
●
┓
┗
┗
┓
┗
┗
┓
┗
┗
I●
┓
●
例 如图,在△ABC中,作一个圆使它与这个三角形三边都相切.
解:1.作∠B、∠C的平分线BE和CF,交点为I;
2.过I作ID⊥BC,垂足为D;
3.以I为圆,以ID为半径作⊙I.
∴ ⊙I就是所求的圆.
A
B
C
I●
┓
●
E
F
D
这样的圆可以作出几个?为什么?.
∵直线BE和CF只有一个交点I,并且点I到 △ABC三边的距离相等(为什么?),
∴因此和△ABC三边都相切的圆可以作出一个,并且只能作一个.
三角形与圆的位置关系
A
B
C
I●
●
┓
┗
┗
E
F
D
三角形与圆的位置关系
和三角形三边都相切的圆叫做三角形的内切圆.这个三角形叫做圆的外切三角形.
内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心.
老师提示:
多边形的边与圆的位置关系称为切.
A
B
C
●
I
A
B
C
I●
●
┓
┗
┗
E
F
D
内心到三角形三边的距离相等.
切线的性质定理的应用
1.已知Rt△ABC的斜边AB=8cm,直角边AC=4cm.
(1)以点C为圆心作圆,当半径为多长时,AB与⊙C 相切?
A
C
B
┐
解:(1)过C作CD⊥AB,垂足为D.
D
┛
∵AB=8cm,AC=4cm.
∴∠A=60°.
因此,当半径长为 cm时,AB与⊙C相切.
∴∠B=30°.
切线的性质定理的应用
1.已知Rt△ABC的斜边AB=8cm,直角边AC=4cm.
(2)以点C为圆心,分别以2cm,4cm为半径作两个圆,这两个圆与AB分别有怎样的位置关系?
当r=4cm时,d
C
B
┐
D
┛
当r=2cm时,d>r,AB与⊙C相离;
解:(2)由(1)可知,圆心到AB的距离d= cm,所以
1.在Rt△ABC中, ∠C= 90°, ∠B= 30°,O为AB上一点, OA=m,⊙O的半径为r。当r与m满足怎样的关系时,
1)AC与⊙O相交?
2)AC与⊙O相切?
3)AC与⊙O相离?
知识技能
C
B
A
O
m
r
1.在Rt△ABC中, ∠C= 90°, ∠B= 30°,O为AB上一点, OA=m,⊙O的半径为r。当r与m满足怎样的关系时,
1)AC与⊙O相交?
2)AC与⊙O相切?
3)AC与⊙O相离?
D
练一练
2. 判断题
3.以三角形的一边为直径的圆恰好与另一边相切,则此三角形是__________三角形
直角
(1) 垂直于圆的半径的直线一定是这个圆的切线.( )
(2) 过圆的半径的外端的直线一定是这个圆的切线 . ( )
×
×
这节课有何收获?!
作业
1.用如下方法可以估测河流的大致宽度:如图,观测者站在岸边O处投下 一块石头,激起的半圆形波纹逐渐向远处扩展,当波纹刚好抵达对岸时,另一观测者记录下波纹沿着观测者所在岸边所扩展的距离,这一距离就是河流的大致宽度,请说明这种方法的合理性。
2. 以边长为3,4,5的三角形的三个顶点为圆心,分别作圆与对边相切,则这三个圆的半径分别是多少?
C
A
B
┐
数学理解
3.为了测量一个光盘的的直径,小明把直尺、光盘和三角尺按图所示放置于桌面上,并量出AB=6cm。这张光盘的直径是多少?
3.为了测量一个光盘的的直径,小明把直尺、光盘和三角尺按图所示放置于桌面上,并量出AB=6cm。这张光盘的直径是多少?
O
C
2
1
3
补充定理
已知:如图,P是⊙O外一点,PA是⊙O的切线,AB是弦.
A
B
P
●O
PA2=PB·PC
C
∠PAB= ∠C
弦切角:
弦与切线的夹角(∠PAB)
弦切角等于它所夹的弧所对的圆周角。
(∠PAB = C= ∠D)
D
1
2
3
如图,圆O中弦AB与CD相交于P,你有什么新发现吗?
·O
D
P
A
C
B
PA·PB=PC·PD
练习
