北师大版九下数学3.7切线长定理课件(共17张PPT)
文档属性
| 名称 | 北师大版九下数学3.7切线长定理课件(共17张PPT) | 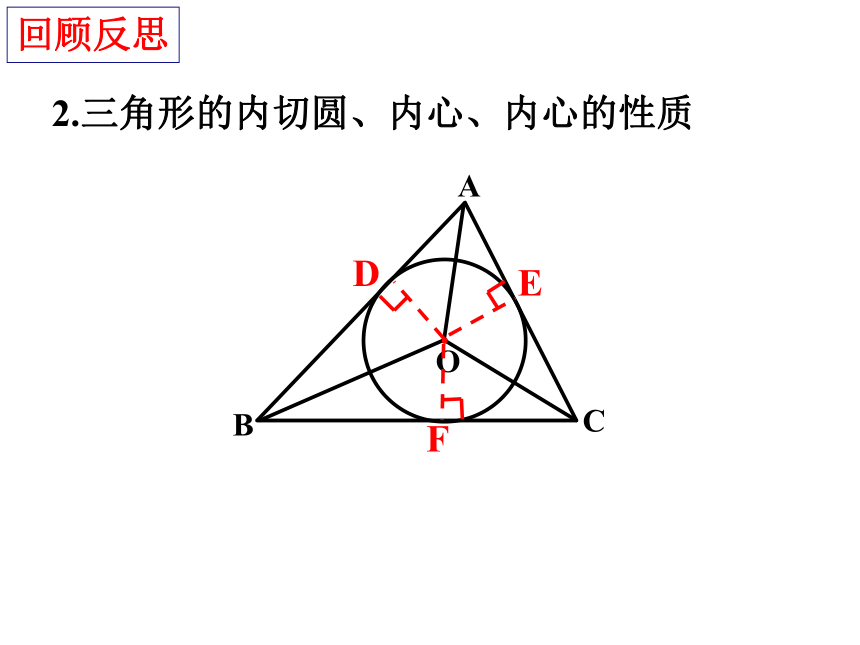 | |
| 格式 | ppt | ||
| 文件大小 | 628.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-17 16:28:58 | ||
图片预览



文档简介
回顾反思
2.三角形的内切圆、内心、内心的性质
D
E
F
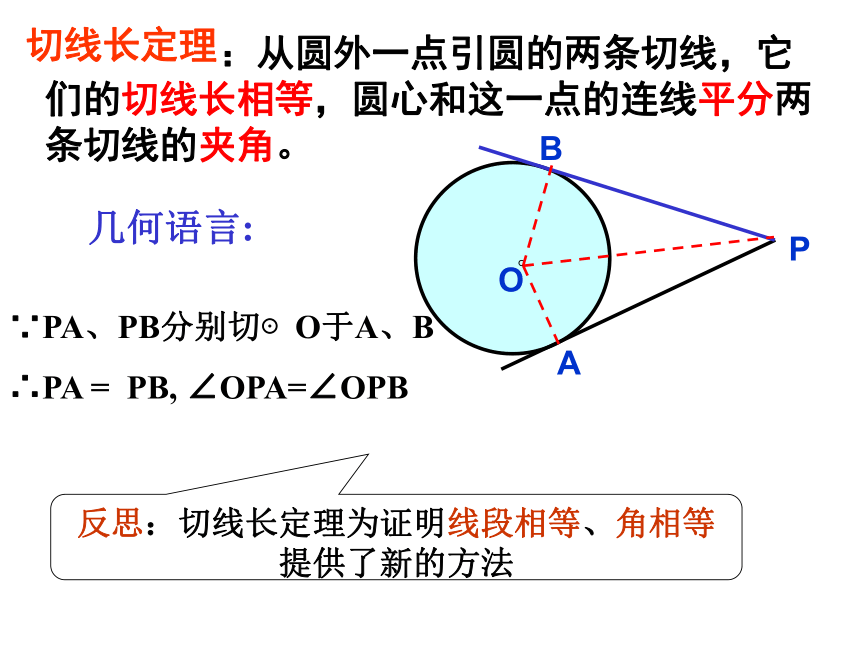
:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。
切线长定理
A
P
O
。
B
几何语言:
反思:切线长定理为证明线段相等、角相等提供了新的方法
∵PA、PB分别切⊙O于A、B
∴PA = PB, ∠OPA=∠OPB
A
B
C
I●
┓
●
E
F
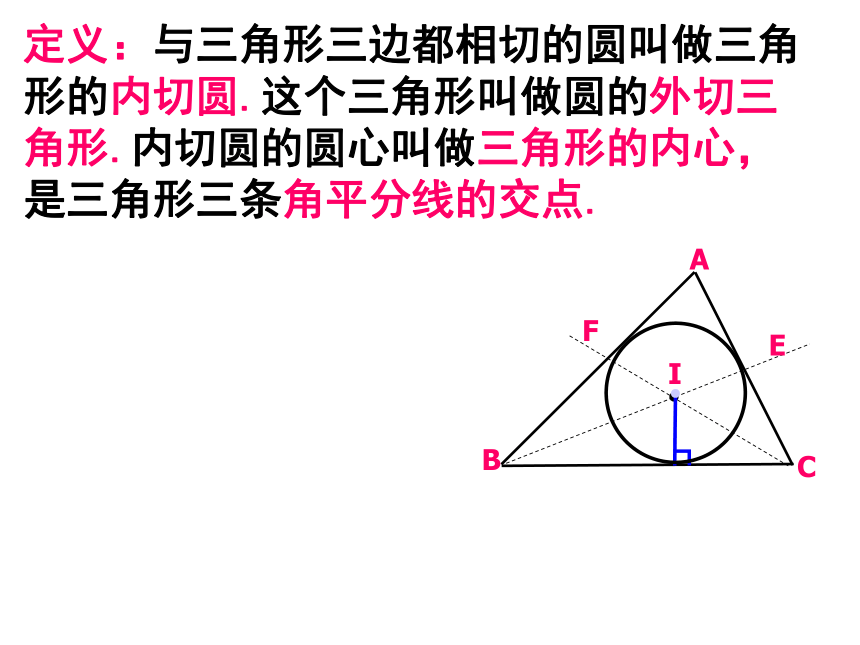
定义:与三角形三边都相切的圆叫做三角形的内切圆.这个三角形叫做圆的外切三角形.内切圆的圆心叫做三角形的内心,是三角形三条角平分线的交点.
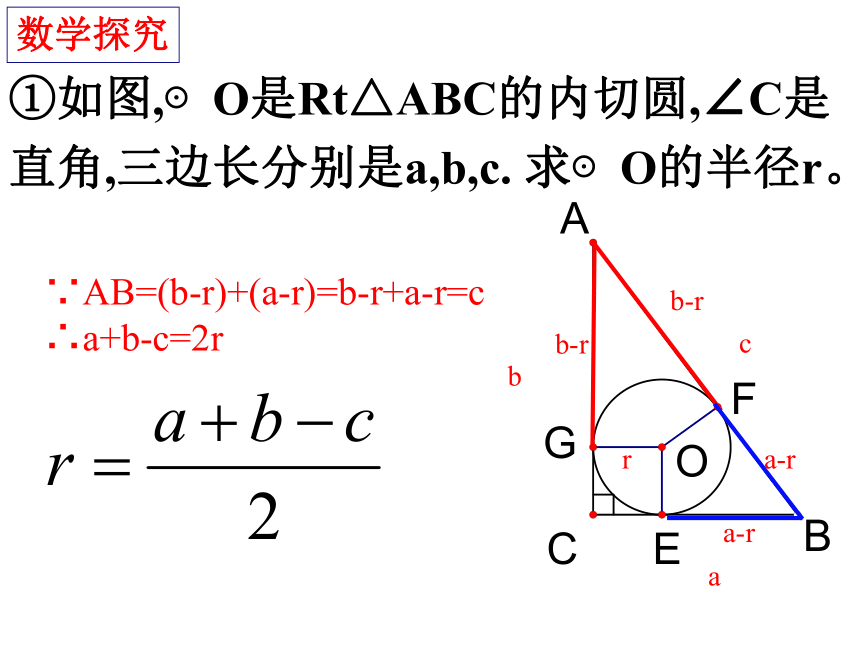
①如图,⊙O是Rt△ABC的内切圆,∠C是
直角,三边长分别是a,b,c. 求⊙O的半径r。
数学探究
a
b
c
r
b-r
b-r
a-r
a-r
∵AB=(b-r)+(a-r)=b-r+a-r=c
∴a+b-c=2r
例1:如图,△ABC中,∠C =90? ,它的内切圆O分别与边AB、BC、CA相切于点D、E、F,且BD=12,AD=8,求⊙O的半径r.
O
E
B
D
C
A
F
例题选讲
r
12
r
12
8
8
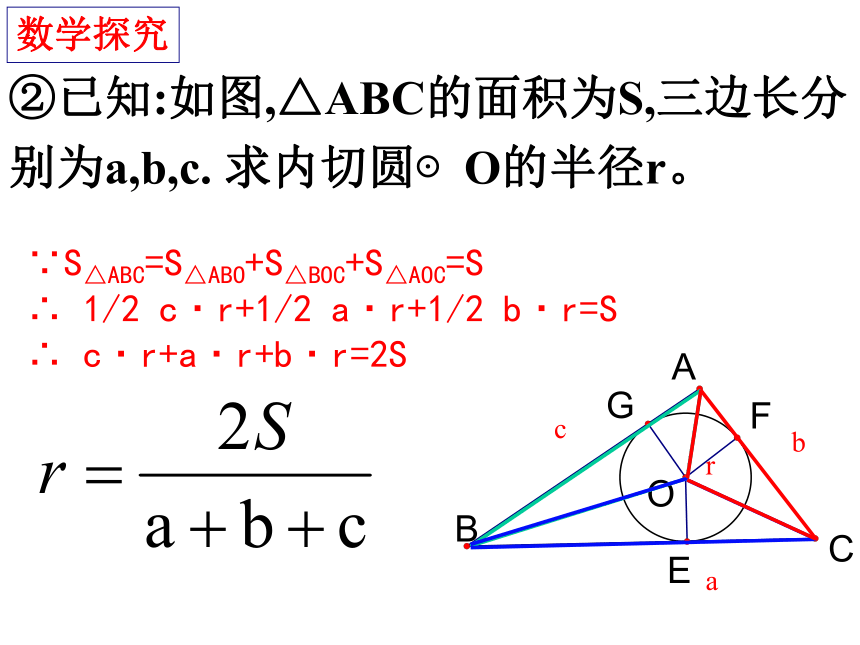
②已知:如图,△ABC的面积为S,三边长分
别为a,b,c. 求内切圆⊙O的半径r。
数学探究
a
b
c
r
∵S△ABC=S△ABO+S△BOC+S△AOC=S
∴ 1/2 c·r+1/2 a·r+1/2 b·r=S
∴ c·r+a·r+b·r=2S
例2:如图,△ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F,且AB=9cm,BC=14cm,CA=13cm,求AF、BD、CE的长。
x
13﹣x
x
13﹣x
9﹣x
9﹣x
例题选讲
A
D
C
B
O
F
E
例3:如图,PA和PB是⊙O的两条切线,A、B为切点,∠P=40°,点D在AB上,且AD=BE,BD=AF,求∠EDF的度数
例题选讲
回顾反思
1.切线长定理
O
B
P
·
·
A
·
从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角。
课后作业
1.已知三角形的周长为10,内切圆的半径为2,则该三角形的面积为 。
2.直角三角形的两个直角边长为7、24,则此三角形ABC的内切圆的半径为 。
3.直角三角形的外接圆半径为5cm,内切圆半径为1cm,则此三角形的周长是_______。
10
3
3
22
5
1
5
(2)观察OP与BC的位置关系,并给予证明。
(1)若OA=3cm, ∠APB=60°,则PA=______.
P
A
B
C
O
M
4、如图,AC为⊙O的直径,PA、PB分别切⊙O于点A、B,OP交⊙O于点M,连结BC。
课后作业
30°
3
(2)观察OP与BC的位置关系,并给予证明。
(1)若OA=3cm, ∠APB=60°,则PA=______.
P
A
B
C
O
M
4、如图,AC为⊙O的直径,PA、PB分别切⊙O于点A、B,OP交⊙O于点M,连结BC。
课后作业
5、已知:如图,PA、PB是⊙O的切线,切点分别是A、B,Q为⊙O上一点,过Q点作⊙O的切线,交PA、PB于E、F点,
(1)已知PA=12cm,求:△PEF的周长
(2)∠P=70°, ∠EOF的大小。
E
A
Q
P
F
B
O
5、已知:如图,PA、PB是⊙O的切线,切点分别是A、B,Q为⊙O上一点,过Q点作⊙O的切线,交PA、PB于E、F点,
(1)已知PA=12cm,求:△PEF的周长
(2)∠P=70°, ∠EOF的大小。
E
A
Q
P
F
B
O
· O
A
B
C
D
E
F
6、如图,AB是⊙O的直径,AD、DC、BC是切线,点A、E、B为切点,若BC=9,AD=4,求OE的长.
方法1
4
4
9
9
5
4
· O
A
B
C
D
E
6、如图,AB是⊙O的直径,AD、DC、BC是切线,点A、E、B为切点,若BC=9,AD=4,求OE的长.
4
9
方法2
2.三角形的内切圆、内心、内心的性质
D
E
F
:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。
切线长定理
A
P
O
。
B
几何语言:
反思:切线长定理为证明线段相等、角相等提供了新的方法
∵PA、PB分别切⊙O于A、B
∴PA = PB, ∠OPA=∠OPB
A
B
C
I●
┓
●
E
F
定义:与三角形三边都相切的圆叫做三角形的内切圆.这个三角形叫做圆的外切三角形.内切圆的圆心叫做三角形的内心,是三角形三条角平分线的交点.
①如图,⊙O是Rt△ABC的内切圆,∠C是
直角,三边长分别是a,b,c. 求⊙O的半径r。
数学探究
a
b
c
r
b-r
b-r
a-r
a-r
∵AB=(b-r)+(a-r)=b-r+a-r=c
∴a+b-c=2r
例1:如图,△ABC中,∠C =90? ,它的内切圆O分别与边AB、BC、CA相切于点D、E、F,且BD=12,AD=8,求⊙O的半径r.
O
E
B
D
C
A
F
例题选讲
r
12
r
12
8
8
②已知:如图,△ABC的面积为S,三边长分
别为a,b,c. 求内切圆⊙O的半径r。
数学探究
a
b
c
r
∵S△ABC=S△ABO+S△BOC+S△AOC=S
∴ 1/2 c·r+1/2 a·r+1/2 b·r=S
∴ c·r+a·r+b·r=2S
例2:如图,△ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F,且AB=9cm,BC=14cm,CA=13cm,求AF、BD、CE的长。
x
13﹣x
x
13﹣x
9﹣x
9﹣x
例题选讲
A
D
C
B
O
F
E
例3:如图,PA和PB是⊙O的两条切线,A、B为切点,∠P=40°,点D在AB上,且AD=BE,BD=AF,求∠EDF的度数
例题选讲
回顾反思
1.切线长定理
O
B
P
·
·
A
·
从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角。
课后作业
1.已知三角形的周长为10,内切圆的半径为2,则该三角形的面积为 。
2.直角三角形的两个直角边长为7、24,则此三角形ABC的内切圆的半径为 。
3.直角三角形的外接圆半径为5cm,内切圆半径为1cm,则此三角形的周长是_______。
10
3
3
22
5
1
5
(2)观察OP与BC的位置关系,并给予证明。
(1)若OA=3cm, ∠APB=60°,则PA=______.
P
A
B
C
O
M
4、如图,AC为⊙O的直径,PA、PB分别切⊙O于点A、B,OP交⊙O于点M,连结BC。
课后作业
30°
3
(2)观察OP与BC的位置关系,并给予证明。
(1)若OA=3cm, ∠APB=60°,则PA=______.
P
A
B
C
O
M
4、如图,AC为⊙O的直径,PA、PB分别切⊙O于点A、B,OP交⊙O于点M,连结BC。
课后作业
5、已知:如图,PA、PB是⊙O的切线,切点分别是A、B,Q为⊙O上一点,过Q点作⊙O的切线,交PA、PB于E、F点,
(1)已知PA=12cm,求:△PEF的周长
(2)∠P=70°, ∠EOF的大小。
E
A
Q
P
F
B
O
5、已知:如图,PA、PB是⊙O的切线,切点分别是A、B,Q为⊙O上一点,过Q点作⊙O的切线,交PA、PB于E、F点,
(1)已知PA=12cm,求:△PEF的周长
(2)∠P=70°, ∠EOF的大小。
E
A
Q
P
F
B
O
· O
A
B
C
D
E
F
6、如图,AB是⊙O的直径,AD、DC、BC是切线,点A、E、B为切点,若BC=9,AD=4,求OE的长.
方法1
4
4
9
9
5
4
· O
A
B
C
D
E
6、如图,AB是⊙O的直径,AD、DC、BC是切线,点A、E、B为切点,若BC=9,AD=4,求OE的长.
4
9
方法2
