北师大版七年级数学下册 1.6.2完全平方公式的应用 (21ppt)
文档属性
| 名称 | 北师大版七年级数学下册 1.6.2完全平方公式的应用 (21ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 422.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-17 13:36:22 | ||
图片预览




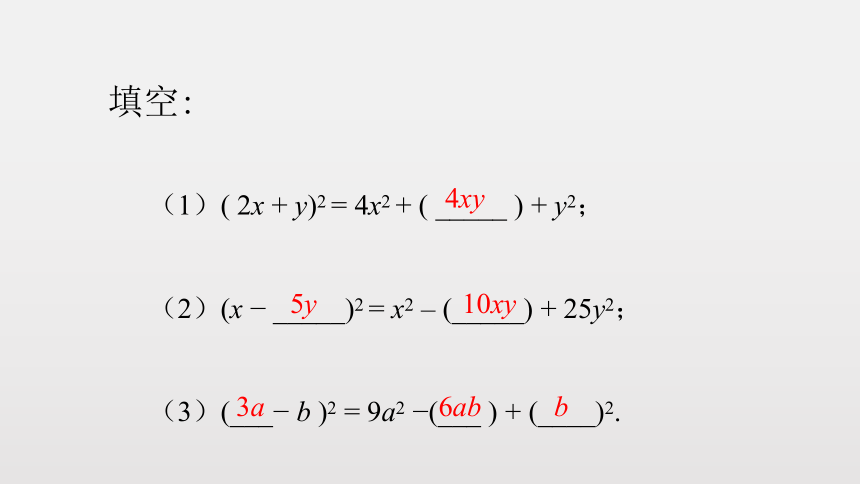




文档简介
第 一章 整式的乘除
第一章 整式的乘除
1.6 完全平方公式
第2课时
学 习 目 标
1.进一步掌握完全平方公式;(重点)
2.灵活运用完全平方公式进行计算.(难点)
提问:
(1) 什么是平方差公式?
(2) 什么是完全平方公式?
(3)语言叙述这两个公式?
复习导入
(a+b)(a-b)=a2-b2
(a+b)2=a2+2ab+b2,
(a-b)2=a2-2ab+b2.
【基础梳理】
1.完全平方公式
(1)语言叙述:两数和(或差)的平方,等于这两个数的平方和,加上(或减去)这两个数的积的2倍.
(2)字母表示:
(a+b)2=a2+2ab+b2,(a-b)2=a2-2ab+b2.
口诀:首平方,尾平方,二倍乘积放中央,符号跟前一个样.
2.完全平方公式的结构特点
公式的左边是一个二项式的平方;公式的右边是一个三项式.
3.推广:公式中的字母a,b可以表示具体的数,也可以表示单项式或多项式.
复习导入
填空:
(1)( 2x + y)2 = 4x2 + ( _____ ) + y2;
(2)(x ? _____)2 = x2 – (_____) + 25y2;
(3)(___? b )2 = 9a2 ?(___ ) + (____)2.
4xy
5y
10xy
3a
b
6ab
思考:怎样计算1022,1972更简便呢?
(1) 1022;
解:原式= (100+2)2
=10000+400+4
=10404.
(2) 1972.
解:原式= (200 –3)2
= (100)2+2×100×2+22
= (200)2-2×200×3+32
= 40000-1200400+9
= 38809.
类型一:利用完全平方公式进行简便运算
例1
方法总结:运用完全平方公式进行简便计算,要熟记完全平方公式的特征,将原式转化为能利用完全平方公式的形式.
(1)982-101×99; (2)20162-2016×4030+20152.
练一练1:
=(2016-2015)2
=1.
解:(1)原式=(100-2)2-(100+1)(100-1)
=1002-400+4-1002+1
=-395.
(2)原式=20162-2×2016×2015+20152
=1002-2×100×2+22-(1002-1)
计算:(1) (x+3)2-x2 ;
例2
你能用几种方法进行计算?试一试。
解: (1) 方法一
完全平方公式 ?合并同类项
(x+3)2-x2
=x2+6x+9-x2
=6x+9
方法二
平方差公式?单项式乘多项式.
(x+3)2-x2
=(x+3+x)(x+3-x)
=(2x+3)·3=6x+9
类型二:综合运用完全平方公式与平方差公式进行计算
(2)(a+b+3)(a+b-3);
(2)(a+b+3)(a+b-3)=[(a+b)+3][(a+b)-3]
=(a+b)2-32
=a2+2ab+b2-9
若不用一般的多项式乘以多项式 ,
怎样用公式来计算 ?
解:
温馨提示:将(a+b)看作一个整体,解题中渗透了整体的思想
(3)(x+5)2 –(x-2)(x-3)
解:
(3)(x+5)2-(x-2)(x-3)= x2+10x +25-(x2-5x+6)
= 15x+19
温馨提示:
1.注意运算的顺序。
2.(x?2)(x?3)展开后的结果要注意添括号。
(a+b+c) (a+b?c); (2) (a+b-c) (a-b?c);
(3) (a-b+c) (a-b?c); (4) (a-b-c) (-a+b?c);
?
?
?
?
练一练2:(注意比较异同):
做一做
有一位老人非常喜欢孩子,每当有孩子到他家做客时,老人都要拿出糖果招待他们。
来一个孩子,老人就给这个孩子一块糖,来两个孩子,老人就给每个孩子两块糖,来三个,就给每人三块糖,……
(1) 第一天有 a 个男孩一起去了老人家,老人一共给了这些孩子多少块糖?
a2
(2) 第二天有 b个女孩一起去了老人家,老人一共给了这些孩子多少块糖?
b2
(3) 第三天这(a+b)个孩子一起去看老人,老人一共给了这些孩子多少块糖?
(a+b)2
(4) 这些孩子第三天得到的糖果数与前两天他们得到的糖果总数哪个多?
第三天多;
多多少?
为什么?
∵(a+b)2=a2 + 2ab + b2
∴(a+b)2—(a2 + b2 ) = 2ab
2ab
已知x-y=6,xy=-8,求:
(1) x2+y2的值; (2)(x+y)2的值.
=36-16=20.
解:(1)∵x-y=6,xy=-8,
(x-y)2=x2+y2-2xy,
∴x2+y2=(x-y)2+2xy
(2)∵x2+y2=20,xy=-8,
∴(x+y)2=x2+y2+2xy
=20-16=4.
例3
类型三:完全平方公式的变形技巧
补充延伸:由(a+b)2 = a2 + 2ab + b2
(a-b)2 = a2 - 2ab + b2
?
?
?
?
?
?
(1). 已知(a-b)2=13,ab= 3,则a+b= .
(2). 已知(a+b)2=5,(a-b)2=6,则a2+b2= .
(a+b)2=(a-b)2+4ab=13+12=25,
a+b=±5.
±5
(a+b)2+(a-b)2=2a2 +2b2 =5+6=11,
?
?
?
练一练3:
4. 若a+b=5,ab=-6,求a2-ab+b2.
解:∵ (a+b)2 = a2 + 2ab + b2 , a+b=5,ab=-6
∴a2+b2=(a+b)2-2ab=52-2×(-6)=37
解:∵x+y=8,∴(x+y)2=64,即x2+y2+2xy=64①
∵x-y=4, ∴(x-y)2=16,即x2+y2-2xy=16②
①-②,得
4xy=48
∴xy=12
∴a2-ab+b2=a2+b2-ab=37-(-6)=43
练一练:
5. 已知x+y=8,x-y=4,求 xy和x2+y2的值.
①+②,得
2(x2+y2)=64+16=80
∴x2+y2=40
类型四:配方法
例5
1.已知x2 ? 4x+y2+6y+13=0,求x+y的值.
解:
原等式可化为:x2 ? 4x+4+y2+6y+9=(x-2)2+(y+3)2 =0
∵(x-2)2≥0,(y+3)2≥0,且(x-2)2+(y+3)2 =0
∴x-2=0,y+3=0
∴x=2,y=-3
∴x+y=-1
练一练6:
已知x2 +2x+y2 ? 6y+10=0,求x与y的值.
原等式可化为:x2+2x+1+y2-6y+9=(x+1)2+(y-3)2 =0
∵(x+1)2≥0,(y-3)2≥0,且(x+1)2+(y-3)2 =0
∴x+1=0,y-3=0
∴x=-1,y=3
解:
课堂小结
完全平方公式
法则
注意
(a±b)2= a2 ±2ab+b2
1.项数、符号、字母及其指数;
常用
结论
2.弄清完全平方公式和平方差公式不同(从公式结构特点及结果两方面).
a2+b2=(a+b)2-2ab=(a-b)2+2ab;
4ab=(a+b)2-(a-b)2.
作业:1、名校课堂P19-20
2、课本P27随堂练习和习题1.12
再见
第一章 整式的乘除
1.6 完全平方公式
第2课时
学 习 目 标
1.进一步掌握完全平方公式;(重点)
2.灵活运用完全平方公式进行计算.(难点)
提问:
(1) 什么是平方差公式?
(2) 什么是完全平方公式?
(3)语言叙述这两个公式?
复习导入
(a+b)(a-b)=a2-b2
(a+b)2=a2+2ab+b2,
(a-b)2=a2-2ab+b2.
【基础梳理】
1.完全平方公式
(1)语言叙述:两数和(或差)的平方,等于这两个数的平方和,加上(或减去)这两个数的积的2倍.
(2)字母表示:
(a+b)2=a2+2ab+b2,(a-b)2=a2-2ab+b2.
口诀:首平方,尾平方,二倍乘积放中央,符号跟前一个样.
2.完全平方公式的结构特点
公式的左边是一个二项式的平方;公式的右边是一个三项式.
3.推广:公式中的字母a,b可以表示具体的数,也可以表示单项式或多项式.
复习导入
填空:
(1)( 2x + y)2 = 4x2 + ( _____ ) + y2;
(2)(x ? _____)2 = x2 – (_____) + 25y2;
(3)(___? b )2 = 9a2 ?(___ ) + (____)2.
4xy
5y
10xy
3a
b
6ab
思考:怎样计算1022,1972更简便呢?
(1) 1022;
解:原式= (100+2)2
=10000+400+4
=10404.
(2) 1972.
解:原式= (200 –3)2
= (100)2+2×100×2+22
= (200)2-2×200×3+32
= 40000-1200400+9
= 38809.
类型一:利用完全平方公式进行简便运算
例1
方法总结:运用完全平方公式进行简便计算,要熟记完全平方公式的特征,将原式转化为能利用完全平方公式的形式.
(1)982-101×99; (2)20162-2016×4030+20152.
练一练1:
=(2016-2015)2
=1.
解:(1)原式=(100-2)2-(100+1)(100-1)
=1002-400+4-1002+1
=-395.
(2)原式=20162-2×2016×2015+20152
=1002-2×100×2+22-(1002-1)
计算:(1) (x+3)2-x2 ;
例2
你能用几种方法进行计算?试一试。
解: (1) 方法一
完全平方公式 ?合并同类项
(x+3)2-x2
=x2+6x+9-x2
=6x+9
方法二
平方差公式?单项式乘多项式.
(x+3)2-x2
=(x+3+x)(x+3-x)
=(2x+3)·3=6x+9
类型二:综合运用完全平方公式与平方差公式进行计算
(2)(a+b+3)(a+b-3);
(2)(a+b+3)(a+b-3)=[(a+b)+3][(a+b)-3]
=(a+b)2-32
=a2+2ab+b2-9
若不用一般的多项式乘以多项式 ,
怎样用公式来计算 ?
解:
温馨提示:将(a+b)看作一个整体,解题中渗透了整体的思想
(3)(x+5)2 –(x-2)(x-3)
解:
(3)(x+5)2-(x-2)(x-3)= x2+10x +25-(x2-5x+6)
= 15x+19
温馨提示:
1.注意运算的顺序。
2.(x?2)(x?3)展开后的结果要注意添括号。
(a+b+c) (a+b?c); (2) (a+b-c) (a-b?c);
(3) (a-b+c) (a-b?c); (4) (a-b-c) (-a+b?c);
?
?
?
?
练一练2:(注意比较异同):
做一做
有一位老人非常喜欢孩子,每当有孩子到他家做客时,老人都要拿出糖果招待他们。
来一个孩子,老人就给这个孩子一块糖,来两个孩子,老人就给每个孩子两块糖,来三个,就给每人三块糖,……
(1) 第一天有 a 个男孩一起去了老人家,老人一共给了这些孩子多少块糖?
a2
(2) 第二天有 b个女孩一起去了老人家,老人一共给了这些孩子多少块糖?
b2
(3) 第三天这(a+b)个孩子一起去看老人,老人一共给了这些孩子多少块糖?
(a+b)2
(4) 这些孩子第三天得到的糖果数与前两天他们得到的糖果总数哪个多?
第三天多;
多多少?
为什么?
∵(a+b)2=a2 + 2ab + b2
∴(a+b)2—(a2 + b2 ) = 2ab
2ab
已知x-y=6,xy=-8,求:
(1) x2+y2的值; (2)(x+y)2的值.
=36-16=20.
解:(1)∵x-y=6,xy=-8,
(x-y)2=x2+y2-2xy,
∴x2+y2=(x-y)2+2xy
(2)∵x2+y2=20,xy=-8,
∴(x+y)2=x2+y2+2xy
=20-16=4.
例3
类型三:完全平方公式的变形技巧
补充延伸:由(a+b)2 = a2 + 2ab + b2
(a-b)2 = a2 - 2ab + b2
?
?
?
?
?
?
(1). 已知(a-b)2=13,ab= 3,则a+b= .
(2). 已知(a+b)2=5,(a-b)2=6,则a2+b2= .
(a+b)2=(a-b)2+4ab=13+12=25,
a+b=±5.
±5
(a+b)2+(a-b)2=2a2 +2b2 =5+6=11,
?
?
?
练一练3:
4. 若a+b=5,ab=-6,求a2-ab+b2.
解:∵ (a+b)2 = a2 + 2ab + b2 , a+b=5,ab=-6
∴a2+b2=(a+b)2-2ab=52-2×(-6)=37
解:∵x+y=8,∴(x+y)2=64,即x2+y2+2xy=64①
∵x-y=4, ∴(x-y)2=16,即x2+y2-2xy=16②
①-②,得
4xy=48
∴xy=12
∴a2-ab+b2=a2+b2-ab=37-(-6)=43
练一练:
5. 已知x+y=8,x-y=4,求 xy和x2+y2的值.
①+②,得
2(x2+y2)=64+16=80
∴x2+y2=40
类型四:配方法
例5
1.已知x2 ? 4x+y2+6y+13=0,求x+y的值.
解:
原等式可化为:x2 ? 4x+4+y2+6y+9=(x-2)2+(y+3)2 =0
∵(x-2)2≥0,(y+3)2≥0,且(x-2)2+(y+3)2 =0
∴x-2=0,y+3=0
∴x=2,y=-3
∴x+y=-1
练一练6:
已知x2 +2x+y2 ? 6y+10=0,求x与y的值.
原等式可化为:x2+2x+1+y2-6y+9=(x+1)2+(y-3)2 =0
∵(x+1)2≥0,(y-3)2≥0,且(x+1)2+(y-3)2 =0
∴x+1=0,y-3=0
∴x=-1,y=3
解:
课堂小结
完全平方公式
法则
注意
(a±b)2= a2 ±2ab+b2
1.项数、符号、字母及其指数;
常用
结论
2.弄清完全平方公式和平方差公式不同(从公式结构特点及结果两方面).
a2+b2=(a+b)2-2ab=(a-b)2+2ab;
4ab=(a+b)2-(a-b)2.
作业:1、名校课堂P19-20
2、课本P27随堂练习和习题1.12
再见
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
