北师大版七年级下册数学 6.3 等可能事件的概率计算 课件 (共26张PPT)
文档属性
| 名称 | 北师大版七年级下册数学 6.3 等可能事件的概率计算 课件 (共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-17 09:14:46 | ||
图片预览





文档简介
等可能事件的概率
概
率
北师大版七年级下册第六章《概率初步》第三节《等可能事件概率》第三课时
小组热身赛开始
认真审题
稳中求胜
注重方法
小心陷阱
1
3
2
4
长方体盒子里有7个球,摸出黄球的概率为( )
摸出红球的概率为( )
小球在如图的地板上自由地滚动,它最终停留在白色方砖上的概率是多少?
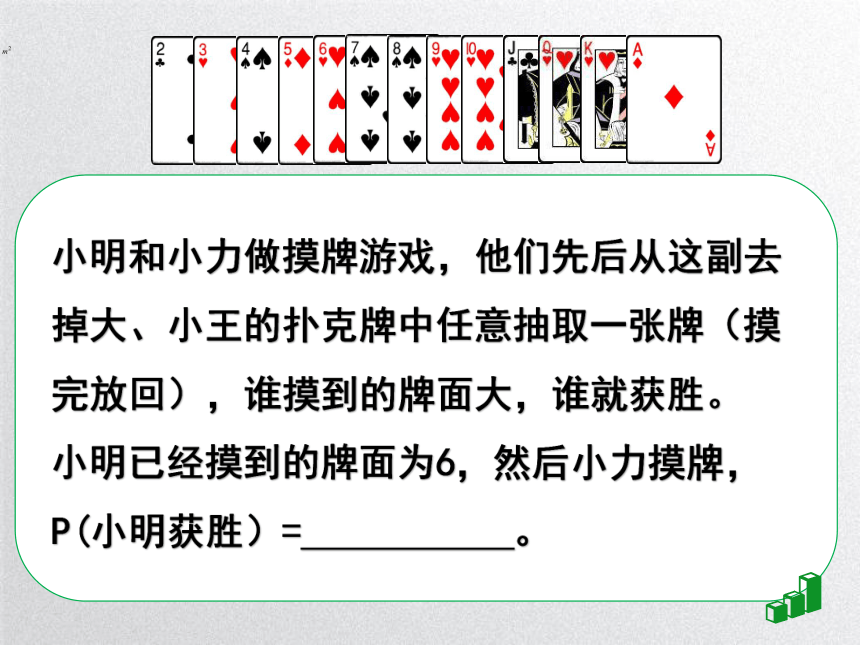
小明和小力做摸牌游戏,他们先后从这副去掉大、小王的扑克牌中任意抽取一张牌(摸完放回),谁摸到的牌面大,谁就获胜。现小明已经摸到的牌面为6,然后小力摸牌,
P(小明获胜)= 。
任意掷一枚均匀的骰子。
(1)P(掷出的点数小于3)=
(2)P(掷出的点数是7)=
教学目标
1
知识目标
2
3
能力目标
情感目标
掌握
等可能事件概率的大小与面积的关系。
能够
设计符合要求的简单概率模型。
感受
概率的应用价值。
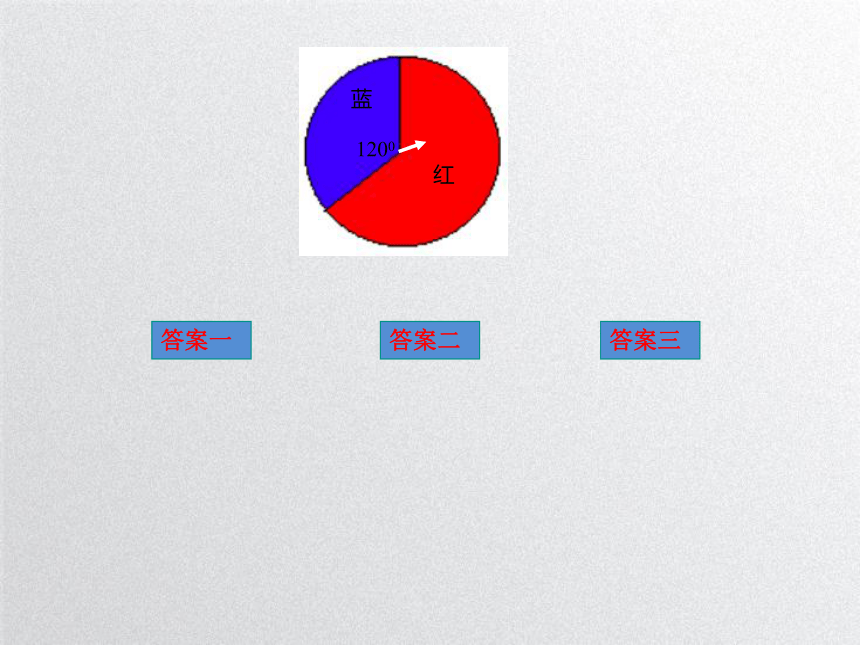
如图是一个可以自由转动的转盘, 转动转盘,当转盘停止时,指针落
在蓝色区域和红色区域的概率分别
是多少?
探究(一):概率的大小与面积的关系
1200
红
蓝
先独立思考、书写答案,然后小组交流
1200
红
蓝
答案一
答案二
答案三
1200
红
蓝
答案一
答案三
答案二
先把红色区域等分成2份,
这样转盘被分成3个等大扇形区域,
其中1个是蓝色, 2个是红色,
所以P(落在蓝色区域)= ,
P(落在红色区域)= 。
1200
红
蓝
答案一
答案三
答案二
利用圆心角度数计算,
P(落在蓝色区域)= , P(落在红色区域)=
1200
红
蓝
答案一
答案三
答案二
指针不是落在蓝色区域就是落在红色区域,落在蓝色色区域和红色区域的概率相等,
所以P(落在蓝色区域)=
P(落在红色区域)= 。
.
探究(二)逆向思维,设计概率大小类型题。
如图:转盘被等分成18个扇形,请在转盘的适当地方涂上颜色,使得自由转动这个转盘,当它停止转动时,指针落在红色区域的概率为 ,蓝色区域的概率为 ,
黄色区域的概率为 吗?
思维导图
概率
摸球
摸牌
掷骰子
转盘
等可能事件
小组竞赛
01
02
03
04
05
06
认真审题,注重语言表达
思考题
总结
一位汽车司机准备去商场购物,然后他随意把
汽车停在某个停车场内,停车场内一个停车位
置正好占一个方格且一个方格除颜色外完全一
样,则汽车停在蓝色区域的概率( )
一张写有密码的纸片被随意地埋在
下面矩形区域内(每个格大小相同)
(1)埋在哪个区域的可能性大?
(2)分别计算出埋在三个区域内的概率;
(3)埋在哪两个区域的概率相同。
A B C
如图是一个转盘,扇形1,2,3,4,5所对的圆心角分别是180°,90°,45°,30°,15°,任意转动转盘,求出指针分别指向1,2,3,4,5的概率。(指针恰好指向两扇形交线的概率视为零)。
小红和小明在操场上做游戏,他们先在地上画了半径为2m和3m的同心圆(如图),蒙上眼睛在一定距离外向圆内扔小石子,投中阴影小红胜,否则小明胜,未扔入圆内不算,请你帮他们计算小红和小明获胜的概率各是多少?
某电视频道播放正片与广告的时间之比为7:1,广告随机穿插在正片之间,小明随机地打开电视机,收看该频道,他开机就能看到正片的概率是多少?
如图是一个转盘,小颖认为转盘上共有三种不同的颜色,所以自由转动这个转盘,指针停在红色、黄色、或蓝色区域的概率都是 你认为呢?
思考题1
一只蚂蚁在如图所示的七巧板上任意爬行,已知它停在这副七巧板上的任一点的可能性相同,求停在黄颜色,粉颜色板上的概率。
中考闯关
我学会了
还有不足
意外收获
谈谈你的收获
等可能事件
概率
等面积
通过概率求面积
本节课堂精炼
预习下一课时
作 业
谢谢聆听
概
率
北师大版七年级下册第六章《概率初步》第三节《等可能事件概率》第三课时
小组热身赛开始
认真审题
稳中求胜
注重方法
小心陷阱
1
3
2
4
长方体盒子里有7个球,摸出黄球的概率为( )
摸出红球的概率为( )
小球在如图的地板上自由地滚动,它最终停留在白色方砖上的概率是多少?
小明和小力做摸牌游戏,他们先后从这副去掉大、小王的扑克牌中任意抽取一张牌(摸完放回),谁摸到的牌面大,谁就获胜。现小明已经摸到的牌面为6,然后小力摸牌,
P(小明获胜)= 。
任意掷一枚均匀的骰子。
(1)P(掷出的点数小于3)=
(2)P(掷出的点数是7)=
教学目标
1
知识目标
2
3
能力目标
情感目标
掌握
等可能事件概率的大小与面积的关系。
能够
设计符合要求的简单概率模型。
感受
概率的应用价值。
如图是一个可以自由转动的转盘, 转动转盘,当转盘停止时,指针落
在蓝色区域和红色区域的概率分别
是多少?
探究(一):概率的大小与面积的关系
1200
红
蓝
先独立思考、书写答案,然后小组交流
1200
红
蓝
答案一
答案二
答案三
1200
红
蓝
答案一
答案三
答案二
先把红色区域等分成2份,
这样转盘被分成3个等大扇形区域,
其中1个是蓝色, 2个是红色,
所以P(落在蓝色区域)= ,
P(落在红色区域)= 。
1200
红
蓝
答案一
答案三
答案二
利用圆心角度数计算,
P(落在蓝色区域)= , P(落在红色区域)=
1200
红
蓝
答案一
答案三
答案二
指针不是落在蓝色区域就是落在红色区域,落在蓝色色区域和红色区域的概率相等,
所以P(落在蓝色区域)=
P(落在红色区域)= 。
.
探究(二)逆向思维,设计概率大小类型题。
如图:转盘被等分成18个扇形,请在转盘的适当地方涂上颜色,使得自由转动这个转盘,当它停止转动时,指针落在红色区域的概率为 ,蓝色区域的概率为 ,
黄色区域的概率为 吗?
思维导图
概率
摸球
摸牌
掷骰子
转盘
等可能事件
小组竞赛
01
02
03
04
05
06
认真审题,注重语言表达
思考题
总结
一位汽车司机准备去商场购物,然后他随意把
汽车停在某个停车场内,停车场内一个停车位
置正好占一个方格且一个方格除颜色外完全一
样,则汽车停在蓝色区域的概率( )
一张写有密码的纸片被随意地埋在
下面矩形区域内(每个格大小相同)
(1)埋在哪个区域的可能性大?
(2)分别计算出埋在三个区域内的概率;
(3)埋在哪两个区域的概率相同。
A B C
如图是一个转盘,扇形1,2,3,4,5所对的圆心角分别是180°,90°,45°,30°,15°,任意转动转盘,求出指针分别指向1,2,3,4,5的概率。(指针恰好指向两扇形交线的概率视为零)。
小红和小明在操场上做游戏,他们先在地上画了半径为2m和3m的同心圆(如图),蒙上眼睛在一定距离外向圆内扔小石子,投中阴影小红胜,否则小明胜,未扔入圆内不算,请你帮他们计算小红和小明获胜的概率各是多少?
某电视频道播放正片与广告的时间之比为7:1,广告随机穿插在正片之间,小明随机地打开电视机,收看该频道,他开机就能看到正片的概率是多少?
如图是一个转盘,小颖认为转盘上共有三种不同的颜色,所以自由转动这个转盘,指针停在红色、黄色、或蓝色区域的概率都是 你认为呢?
思考题1
一只蚂蚁在如图所示的七巧板上任意爬行,已知它停在这副七巧板上的任一点的可能性相同,求停在黄颜色,粉颜色板上的概率。
中考闯关
我学会了
还有不足
意外收获
谈谈你的收获
等可能事件
概率
等面积
通过概率求面积
本节课堂精炼
预习下一课时
作 业
谢谢聆听
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
