北师大版数学八年级下册课件:1.2.1 勾股定理及其逆定理(共31张PPT)
文档属性
| 名称 | 北师大版数学八年级下册课件:1.2.1 勾股定理及其逆定理(共31张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 680.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-17 00:00:00 | ||
图片预览





文档简介
2 直角三角形
第1课时 勾股定理及其逆定理
北师版八年级数学下册
新课导入
我们学过直角三角形的哪些性质和判定方法?与同伴交流.
A
B
C
想一想
新课探究
(1)直角三角形的两个锐角有怎样的关系?为什么?
(2)如果一个三角形有两个角互余,那么这个三角形是直角三角形吗?为什么?
定理 直角三角形的两个锐角互余.
定理 有两个角互余的三角形是直角三角形.
A
B
C
∵∠B = 90°,
∴∠A +∠C = 90°.
勾股定理 直角三角形两条直角边的平方和等于斜边的平方.
教材中曾利用数方格和割补图形的方法得到了勾股定理.
b
b
a
a
S = a2 + b2
a
c
b
a
c
b
小正方形的面积= (a – b)2
即 c2 = a2 + b2.
= c2 – 4× ab
勾股定理的证明:
D
E
F
G
H
I
A
B
C
a
b
c
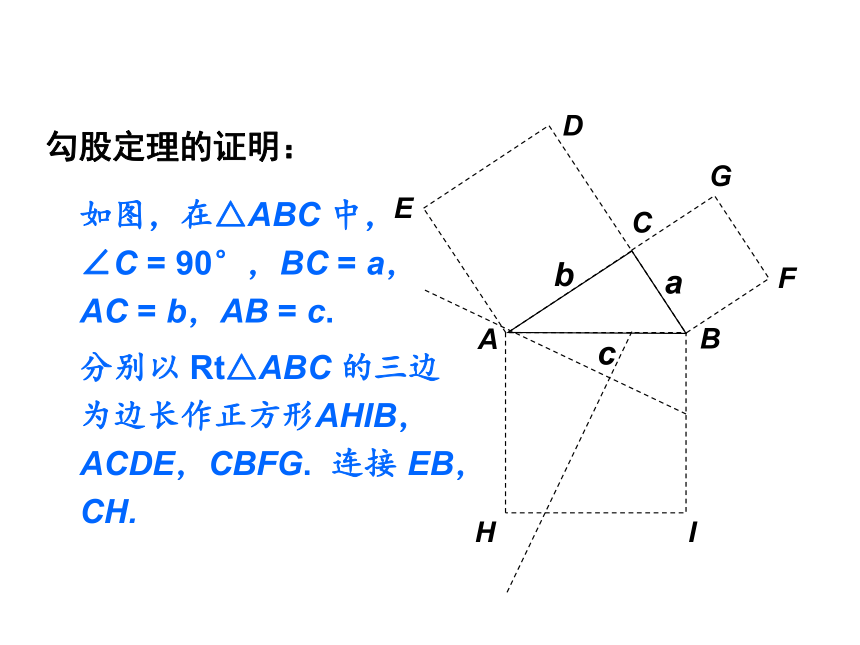
如图,在△ABC 中,∠C = 90°,BC = a,
AC = b,AB = c.
分别以 Rt△ABC 的三边为边长作正方形AHIB,ACDE,CBFG. 连接 EB,CH.
E
F
G
M
N
H
I
A
B
C
a
b
c
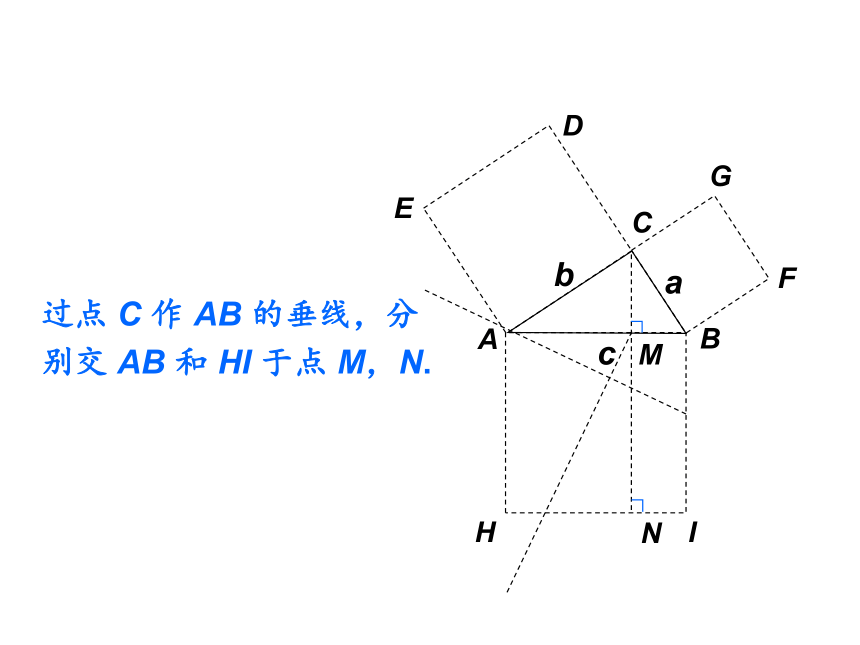
过点 C 作 AB 的垂线,分别交 AB 和 HI 于点 M,N.
D
E
F
G
M
N
H
I
A
B
C
a
b
c
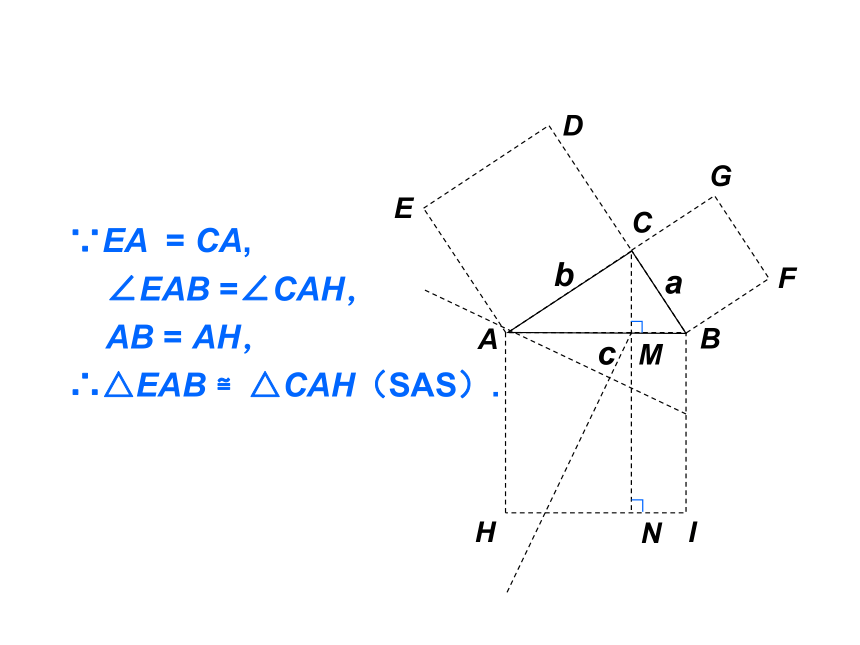
∵EA = CA,
∠EAB =∠CAH,
AB = AH,
∴△EAB ≌△CAH(SAS).
D
E
F
G
M
N
H
I
A
B
C
a
b
c
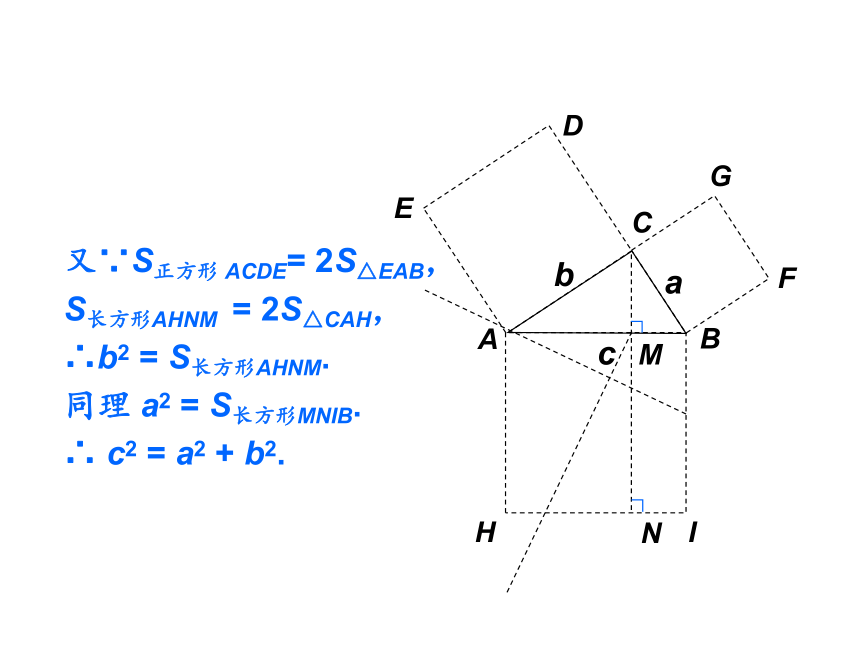
又∵S正方形 ACDE= 2S△EAB,
S长方形AHNM = 2S△CAH,
∴b2 = S长方形AHNM.
同理 a2 = S长方形MNIB.
∴ c2 = a2 + b2.
D
练习
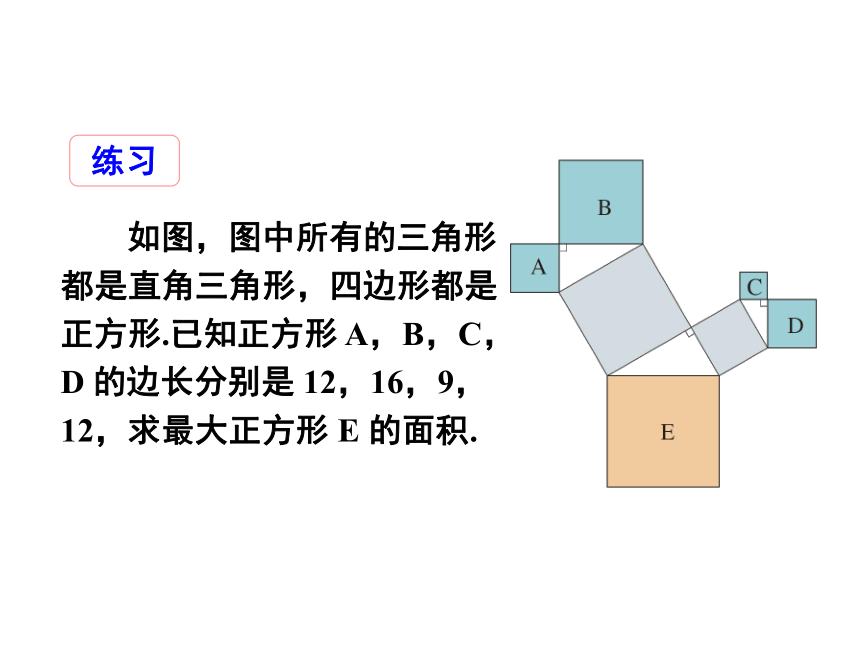
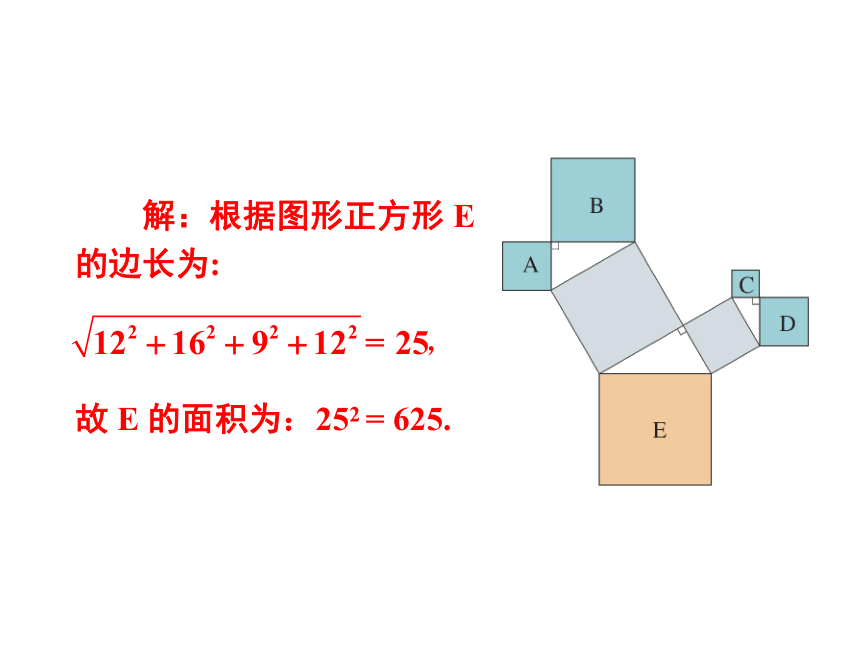
如图,图中所有的三角形都是直角三角形,四边形都是正方形.已知正方形 A,B,C,D 的边长分别是 12,16,9,12,求最大正方形 E 的面积.
解:根据图形正方形 E 的边长为:
故 E 的面积为:252 = 625.
反过来,在一个三角形中,当两边的平方和等于第三边的平方时,我们曾用度量的方法得出“这个三角形是直角三角形”的结论.你能证明此结论吗?
已知:如图,在△ABC 中,AB2 + AC2 = BC2.
求证:△ABC 是直角三角形.
A
B
C
证明:如图作 Rt△A'B'C',
A'
B'
C'
使∠A' = 90°,A'B' = AB,A’C' = AC,
则 A'B'2 + A'C'2 = B'C'2(勾股定理)
∵AB2 + AC2 = BC2,
∴BC2 = B'C'2.
∴BC = B'C'.
∴△ABC ≌ △A'B'C'(SSS).
∴∠A =∠A' = 90°.
因此,△ABC 是直角三角形.
A
B
C
定理 如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
判断下列三边组成的三角形是不是直角三角形.
(1)a = 2,b = 3,c = 4. ( )
(2)a = 9,b = 7,c = 12. ( )
(3)a = 25,b = 20,c = 15. ( )
×
×
√
练习
议一议
观察上面两个命题,它们的条件和结论之间有怎样的关系?在前面的学习中还有类似的命题吗?
上面两个定理的条件和结论互换了位置,即勾股定理的条件是第二个定理的结论,结论是第二个定理的条件.
再观察下面三组命题:
如果两个角是对顶角,那么它们相等;
如果两个角相等,那么它们是对顶角.
如果小明患了肺炎,那么他一定会发烧;
如果小明发烧,那么他一定患了肺炎.
一个三角形中相等的边所对的角相等;
一个三角形中相等的角所对的边相等.
在两个命题中,如果一个命题条件和结论分别是另一个命题的结论和条件,那么这两个命题称为互逆命题,其中一个命题称为另一个命题的逆命题.
想一想
你能写出命题“如果两个有理数相等,那么它们的平方相等”的逆命题吗?它们都是真命题吗?
逆命题:如果两个有理数的平方相等,那么这两个有理数相等.
原命题是真命题,逆命题是假命题.
如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,其中一个定理称为另一个定理的逆定理.
随堂演练
1. 在 Rt△ABC 中,∠C = 90°.
(1)已知 c = 25,b = 15,求 a;
(2)已知 a = ,∠A = 60°,求 b,c.
2. 已知直角三角形的两边长分别为 3,2,求另一条边长.
解:当斜边的长为 3 时,另一条边长
当两条直角边长分别为 3、2时,斜边长
3. 说出下列命题的逆命题,并判断每对命题的真假:
(1)四边形是多边形;
(2)两直线平行,同旁内角互补;
(3)如果 ab = 0,那么 a = 0,b = 0.
解:(1)多边形是四边形.原命题是真,逆命题是假.(2)同旁内角互补,两直线平行.原命题是真,逆命题是真.(3)如果那么 a = 0,
b = 0,那么 ab = 0.原命题是假,逆命题是真.
4. 如图,在四边形 ABCD 中,AB∥CD,E 为 BC 上的一点,且∠BAE = 25°,∠CDE = 65°,AE = 2,DE = 3,求 AD 的长.
解:∵AB∥CD,
∴ ∠BAD +∠ADC = 180°,
又∵∠BAE = 25°,∠CDE = 65°,
∴∠EAD +∠ ADE = 90°,
根据勾股定理,
AD2 = AE2 + DE2 = 22 + 32 = 13,
∴ AD =
解:由题意得:(a + b)(a – b)(a2 + b2 – c2) = 0,∴ a – b = 0 或 a2 + b2 – c2 = 0.
5. 已知 a、b、c 是△ABC 的三边长,且满足
,试判断△ABC 的形状.
当 a = b 时,△ABC 为等腰三角形;
当 a ≠ b 时,△ABC 为直角三角形.
6. 一个零件的形状如图所示,工人师傅量得这个零件各边尺寸如下(单位:dm):AB = 3,AD = 4,BC = 12,CD = 13.且∠DAB = 90°.你能求出这个零件的面积吗?
解:如图,连接 BD. 在Rt△ABD 中,
在△BCD 中,
BD2 + BC2 = 52 + 122 = 132 = CD2.
∴△BCD 为直角三角形,∠DBC = 90°.
课堂小结
定理 直角三角形的两个锐角互余.
定理 有两个角互余的三角形是直角三角形.
勾股定理 直角三角形两条直角边的平方和等于斜边的平方.
定理 如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
互逆命题
互逆命题
第1课时 勾股定理及其逆定理
北师版八年级数学下册
新课导入
我们学过直角三角形的哪些性质和判定方法?与同伴交流.
A
B
C
想一想
新课探究
(1)直角三角形的两个锐角有怎样的关系?为什么?
(2)如果一个三角形有两个角互余,那么这个三角形是直角三角形吗?为什么?
定理 直角三角形的两个锐角互余.
定理 有两个角互余的三角形是直角三角形.
A
B
C
∵∠B = 90°,
∴∠A +∠C = 90°.
勾股定理 直角三角形两条直角边的平方和等于斜边的平方.
教材中曾利用数方格和割补图形的方法得到了勾股定理.
b
b
a
a
S = a2 + b2
a
c
b
a
c
b
小正方形的面积= (a – b)2
即 c2 = a2 + b2.
= c2 – 4× ab
勾股定理的证明:
D
E
F
G
H
I
A
B
C
a
b
c
如图,在△ABC 中,∠C = 90°,BC = a,
AC = b,AB = c.
分别以 Rt△ABC 的三边为边长作正方形AHIB,ACDE,CBFG. 连接 EB,CH.
E
F
G
M
N
H
I
A
B
C
a
b
c
过点 C 作 AB 的垂线,分别交 AB 和 HI 于点 M,N.
D
E
F
G
M
N
H
I
A
B
C
a
b
c
∵EA = CA,
∠EAB =∠CAH,
AB = AH,
∴△EAB ≌△CAH(SAS).
D
E
F
G
M
N
H
I
A
B
C
a
b
c
又∵S正方形 ACDE= 2S△EAB,
S长方形AHNM = 2S△CAH,
∴b2 = S长方形AHNM.
同理 a2 = S长方形MNIB.
∴ c2 = a2 + b2.
D
练习
如图,图中所有的三角形都是直角三角形,四边形都是正方形.已知正方形 A,B,C,D 的边长分别是 12,16,9,12,求最大正方形 E 的面积.
解:根据图形正方形 E 的边长为:
故 E 的面积为:252 = 625.
反过来,在一个三角形中,当两边的平方和等于第三边的平方时,我们曾用度量的方法得出“这个三角形是直角三角形”的结论.你能证明此结论吗?
已知:如图,在△ABC 中,AB2 + AC2 = BC2.
求证:△ABC 是直角三角形.
A
B
C
证明:如图作 Rt△A'B'C',
A'
B'
C'
使∠A' = 90°,A'B' = AB,A’C' = AC,
则 A'B'2 + A'C'2 = B'C'2(勾股定理)
∵AB2 + AC2 = BC2,
∴BC2 = B'C'2.
∴BC = B'C'.
∴△ABC ≌ △A'B'C'(SSS).
∴∠A =∠A' = 90°.
因此,△ABC 是直角三角形.
A
B
C
定理 如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
判断下列三边组成的三角形是不是直角三角形.
(1)a = 2,b = 3,c = 4. ( )
(2)a = 9,b = 7,c = 12. ( )
(3)a = 25,b = 20,c = 15. ( )
×
×
√
练习
议一议
观察上面两个命题,它们的条件和结论之间有怎样的关系?在前面的学习中还有类似的命题吗?
上面两个定理的条件和结论互换了位置,即勾股定理的条件是第二个定理的结论,结论是第二个定理的条件.
再观察下面三组命题:
如果两个角是对顶角,那么它们相等;
如果两个角相等,那么它们是对顶角.
如果小明患了肺炎,那么他一定会发烧;
如果小明发烧,那么他一定患了肺炎.
一个三角形中相等的边所对的角相等;
一个三角形中相等的角所对的边相等.
在两个命题中,如果一个命题条件和结论分别是另一个命题的结论和条件,那么这两个命题称为互逆命题,其中一个命题称为另一个命题的逆命题.
想一想
你能写出命题“如果两个有理数相等,那么它们的平方相等”的逆命题吗?它们都是真命题吗?
逆命题:如果两个有理数的平方相等,那么这两个有理数相等.
原命题是真命题,逆命题是假命题.
如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,其中一个定理称为另一个定理的逆定理.
随堂演练
1. 在 Rt△ABC 中,∠C = 90°.
(1)已知 c = 25,b = 15,求 a;
(2)已知 a = ,∠A = 60°,求 b,c.
2. 已知直角三角形的两边长分别为 3,2,求另一条边长.
解:当斜边的长为 3 时,另一条边长
当两条直角边长分别为 3、2时,斜边长
3. 说出下列命题的逆命题,并判断每对命题的真假:
(1)四边形是多边形;
(2)两直线平行,同旁内角互补;
(3)如果 ab = 0,那么 a = 0,b = 0.
解:(1)多边形是四边形.原命题是真,逆命题是假.(2)同旁内角互补,两直线平行.原命题是真,逆命题是真.(3)如果那么 a = 0,
b = 0,那么 ab = 0.原命题是假,逆命题是真.
4. 如图,在四边形 ABCD 中,AB∥CD,E 为 BC 上的一点,且∠BAE = 25°,∠CDE = 65°,AE = 2,DE = 3,求 AD 的长.
解:∵AB∥CD,
∴ ∠BAD +∠ADC = 180°,
又∵∠BAE = 25°,∠CDE = 65°,
∴∠EAD +∠ ADE = 90°,
根据勾股定理,
AD2 = AE2 + DE2 = 22 + 32 = 13,
∴ AD =
解:由题意得:(a + b)(a – b)(a2 + b2 – c2) = 0,∴ a – b = 0 或 a2 + b2 – c2 = 0.
5. 已知 a、b、c 是△ABC 的三边长,且满足
,试判断△ABC 的形状.
当 a = b 时,△ABC 为等腰三角形;
当 a ≠ b 时,△ABC 为直角三角形.
6. 一个零件的形状如图所示,工人师傅量得这个零件各边尺寸如下(单位:dm):AB = 3,AD = 4,BC = 12,CD = 13.且∠DAB = 90°.你能求出这个零件的面积吗?
解:如图,连接 BD. 在Rt△ABD 中,
在△BCD 中,
BD2 + BC2 = 52 + 122 = 132 = CD2.
∴△BCD 为直角三角形,∠DBC = 90°.
课堂小结
定理 直角三角形的两个锐角互余.
定理 有两个角互余的三角形是直角三角形.
勾股定理 直角三角形两条直角边的平方和等于斜边的平方.
定理 如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
互逆命题
互逆命题
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
