北师大版数学八年级下册课件:3.4.简单的图案设计(共25张PPT)
文档属性
| 名称 | 北师大版数学八年级下册课件:3.4.简单的图案设计(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-17 00:00:00 | ||
图片预览




文档简介
北师版·八年级数学下册
4 简单的图案设计
复习导入
“图形变换”方式 :
图形变换
轴对称变换
平移变换
旋转变换
下面的图案可以看作由什么“基本图案”经过怎样的变换而形成的?
1
2
3
1 可以看成是第一个圆环经过三次平移得到的,平移的距离为圆的直径减去重合部分的长度.
2 第一个C经过两次平移得到的,平移的距离为两个C之间的距离.
3 可以看成是其中一个图形经过两次旋转,每次旋转120°得到的.
进行新课
在生活中,我们经常见到一些美丽的图案:
你能用平移、旋转、轴对称分析图中各图案的形成过程吗?
思考
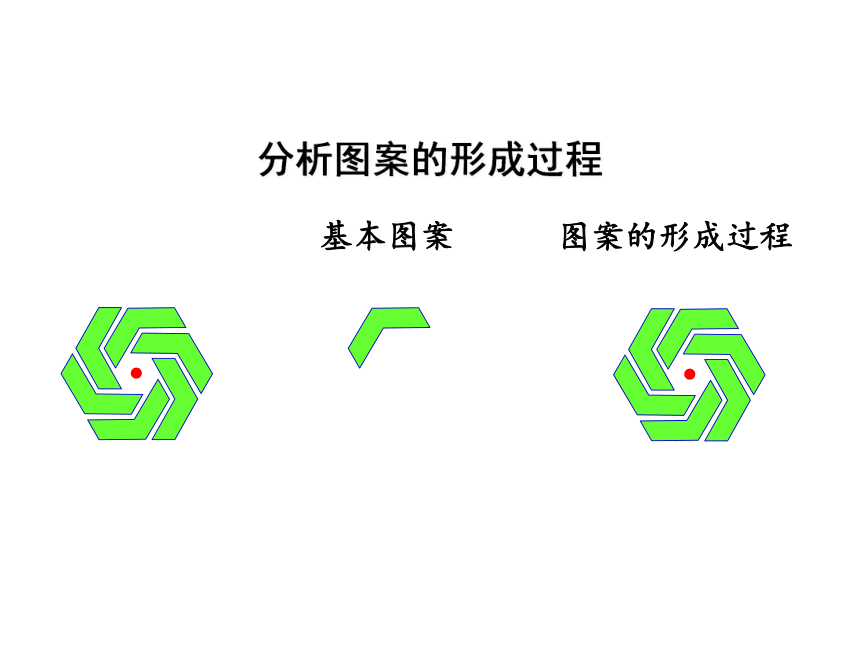
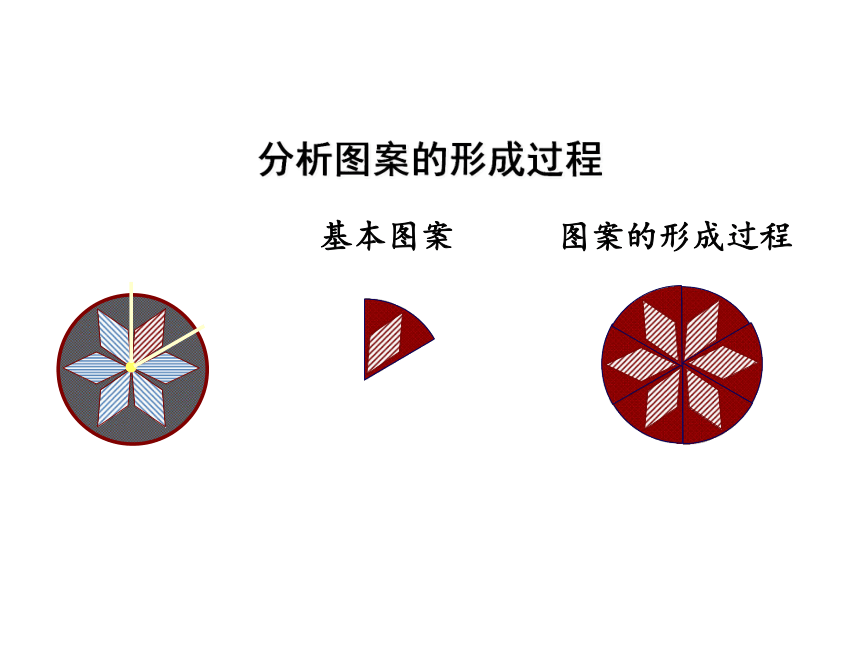
分析图案的形成过程
基本图案
图案的形成过程
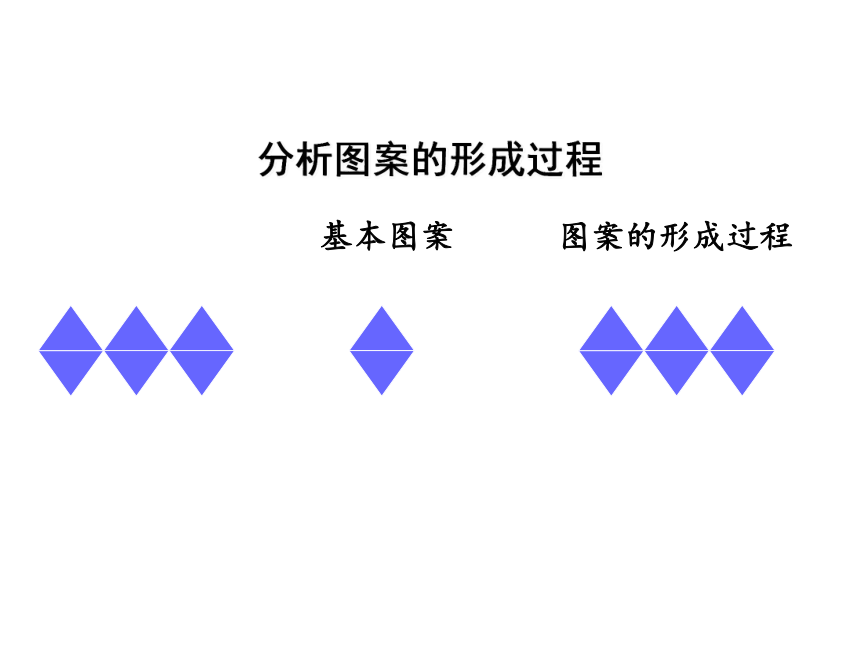
分析图案的形成过程
基本图案
图案的形成过程
分析图案的形成过程
基本图案
图案的形成过程
分析图案的形成过程
基本图案
图案的形成过程
分析图案的形成过程
基本图案
图案的形成过程
分析图案的形成过程
基本图案
图案的形成过程
归纳小结
“图案赏析”方法:
(1) 确定“基本图案”;
(2) 分析轴对称、平移、旋转等变换手法及组合的合理运用.
例 欣赏下图中的图案,并分析这个图案形成的过程.
基本图案有几个?
思考
三种不同颜色的“爬虫”(绿、白、黑),形状、大小完全相同.
1.分析同色“爬虫”、异色“爬虫”之间的关系.
2.若为旋转关系,你能指出“旋转中心”吗?
试一试
在图中,同色的“爬虫”之间是平移关系,所有同色的“爬虫”可以通过其中一只经过平移而得到;相邻的不同色的“爬虫”之间可以通过旋转而得到,其中旋转角为120°,旋转中心为“爬虫”头上、腿上或脚趾上一点.
图案赏析
随堂练习
1.国旗上的四个小五角星,通过怎样的移动可以相互得到( )
A.轴对称 B.平移 C.旋转 D.平移和旋转
2.起重机将重物垂直提起,这可以看作为数学上的( )
A.轴对称 B.平移 C.旋转 D.变形
D
B
3.下图是由12个全等三角形组成的,利用平移、轴对称或旋转分析这个图案的形成过程.
这个图形可以按照以下步骤形成的.
①以一个三角形的一条边为对称轴作与它对称的图形.
②将得到的这组图形以一条边的中点为旋转中心旋转180 °.
③分别以这两组图形为平移的“基本图案”,各平移两次,即可得到最终的图形.
4.仿照下图中的某个标志,每个小组设计一个图案.
课堂小结
1.“图案赏析”方法:
(1) 确定“基本图案”;
(2) 分析轴对称、平移、旋转等变换手法及组合的合理运用.
2.“图案设计”的整体构思:
(1) 突出主题:设计意图要求简捷、自然、别致,具有一定的意义;
(2) 构思图案:确定整幅图案的形状和“基本图案”;
(3) 形成图案:运用图形变换方式将“基本图案”演变成组合图案;
(4) 整理图案:对图案进行适当的修饰.
课后作业
1.完成课本P86 习题3.7;
2.完成练习册本课时的习题.
4 简单的图案设计
复习导入
“图形变换”方式 :
图形变换
轴对称变换
平移变换
旋转变换
下面的图案可以看作由什么“基本图案”经过怎样的变换而形成的?
1
2
3
1 可以看成是第一个圆环经过三次平移得到的,平移的距离为圆的直径减去重合部分的长度.
2 第一个C经过两次平移得到的,平移的距离为两个C之间的距离.
3 可以看成是其中一个图形经过两次旋转,每次旋转120°得到的.
进行新课
在生活中,我们经常见到一些美丽的图案:
你能用平移、旋转、轴对称分析图中各图案的形成过程吗?
思考
分析图案的形成过程
基本图案
图案的形成过程
分析图案的形成过程
基本图案
图案的形成过程
分析图案的形成过程
基本图案
图案的形成过程
分析图案的形成过程
基本图案
图案的形成过程
分析图案的形成过程
基本图案
图案的形成过程
分析图案的形成过程
基本图案
图案的形成过程
归纳小结
“图案赏析”方法:
(1) 确定“基本图案”;
(2) 分析轴对称、平移、旋转等变换手法及组合的合理运用.
例 欣赏下图中的图案,并分析这个图案形成的过程.
基本图案有几个?
思考
三种不同颜色的“爬虫”(绿、白、黑),形状、大小完全相同.
1.分析同色“爬虫”、异色“爬虫”之间的关系.
2.若为旋转关系,你能指出“旋转中心”吗?
试一试
在图中,同色的“爬虫”之间是平移关系,所有同色的“爬虫”可以通过其中一只经过平移而得到;相邻的不同色的“爬虫”之间可以通过旋转而得到,其中旋转角为120°,旋转中心为“爬虫”头上、腿上或脚趾上一点.
图案赏析
随堂练习
1.国旗上的四个小五角星,通过怎样的移动可以相互得到( )
A.轴对称 B.平移 C.旋转 D.平移和旋转
2.起重机将重物垂直提起,这可以看作为数学上的( )
A.轴对称 B.平移 C.旋转 D.变形
D
B
3.下图是由12个全等三角形组成的,利用平移、轴对称或旋转分析这个图案的形成过程.
这个图形可以按照以下步骤形成的.
①以一个三角形的一条边为对称轴作与它对称的图形.
②将得到的这组图形以一条边的中点为旋转中心旋转180 °.
③分别以这两组图形为平移的“基本图案”,各平移两次,即可得到最终的图形.
4.仿照下图中的某个标志,每个小组设计一个图案.
课堂小结
1.“图案赏析”方法:
(1) 确定“基本图案”;
(2) 分析轴对称、平移、旋转等变换手法及组合的合理运用.
2.“图案设计”的整体构思:
(1) 突出主题:设计意图要求简捷、自然、别致,具有一定的意义;
(2) 构思图案:确定整幅图案的形状和“基本图案”;
(3) 形成图案:运用图形变换方式将“基本图案”演变成组合图案;
(4) 整理图案:对图案进行适当的修饰.
课后作业
1.完成课本P86 习题3.7;
2.完成练习册本课时的习题.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
