北师大版数学八年级下册课件:6.2.1平行四边形的判定(1)(共23张PPT)
文档属性
| 名称 | 北师大版数学八年级下册课件:6.2.1平行四边形的判定(1)(共23张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 931.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-17 00:00:00 | ||
图片预览




文档简介
第1课时
平行四边形的判定(1)
北师版·八年级数学下册
2
平行四边形的判定
复习回顾
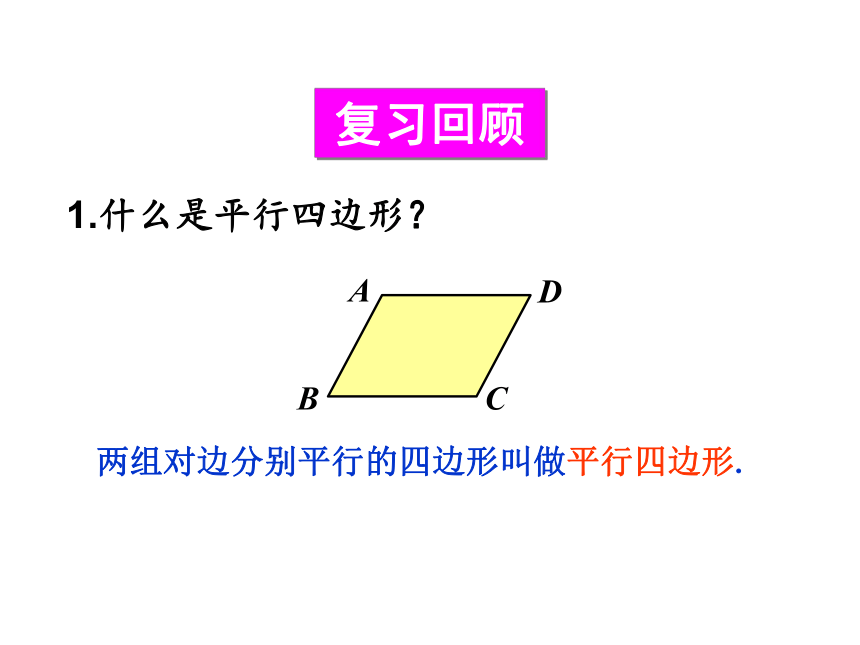
1.什么是平行四边形?
两组对边分别平行的四边形叫做平行四边形.
A
B
C
D
2.我们学行四边形的哪些性质?
平行四边形的两组对边分别相等;
平行四边形的两组对角分别相等;
边
∵四边形ABCD是平行四边形
∴AB=CD,AD=BC
.
角
∵四边形ABCD是平行四边形
∴∠A=∠C,∠D=∠B
.
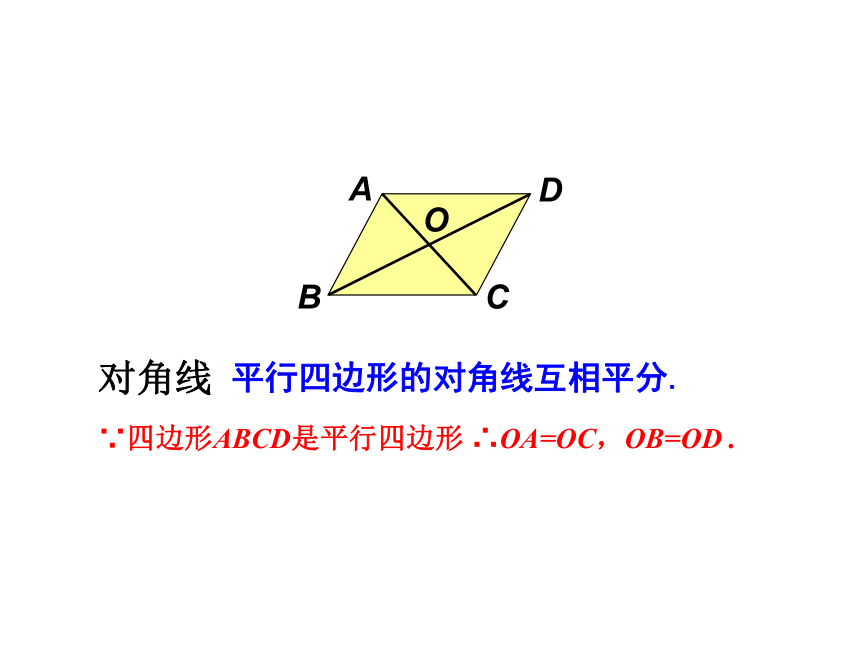
平行四边形的对角线互相平分.
对角线
∵四边形ABCD是平行四边形
∴OA=OC,OB=OD
.
A
B
C
D
O
推进新课
平行四边形的两组对边分别相等;
平行四边形的两组对角分别相等;
平行四边形的对角线互相平分.
讨论
我们已经学行四边形的这些性质,那么它们的逆命题各是什么呢?
两组对角分别相等的四边形是平行四边形;
对角线互相平分的四边形是平行四边形.
两组对边分别相等的四边形是平行四边形;
思考
我们得到的这些逆命题都成立吗?我们一起探讨一下吧!
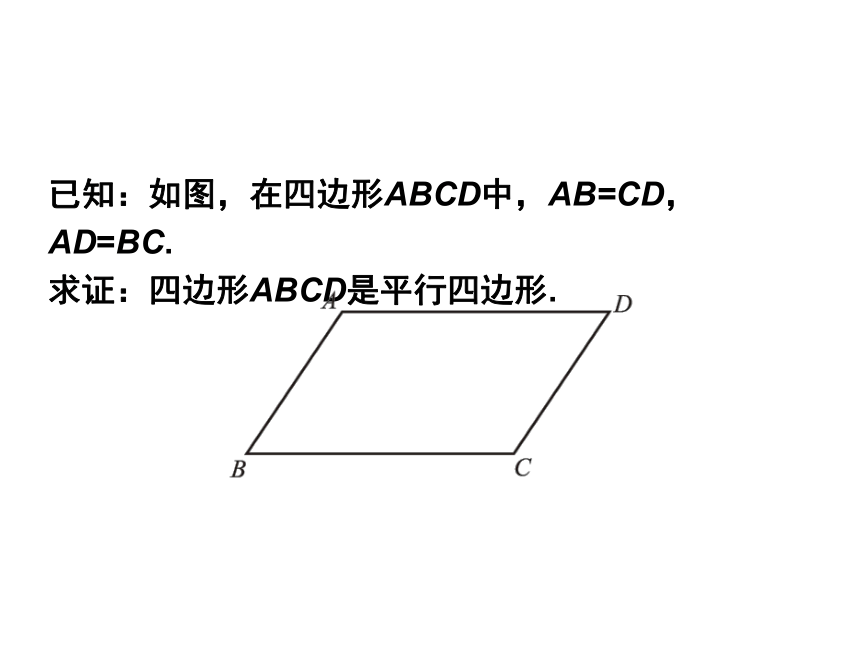
已知:如图,在四边形ABCD中,AB=CD,AD=BC.
求证:四边形ABCD是平行四边形.
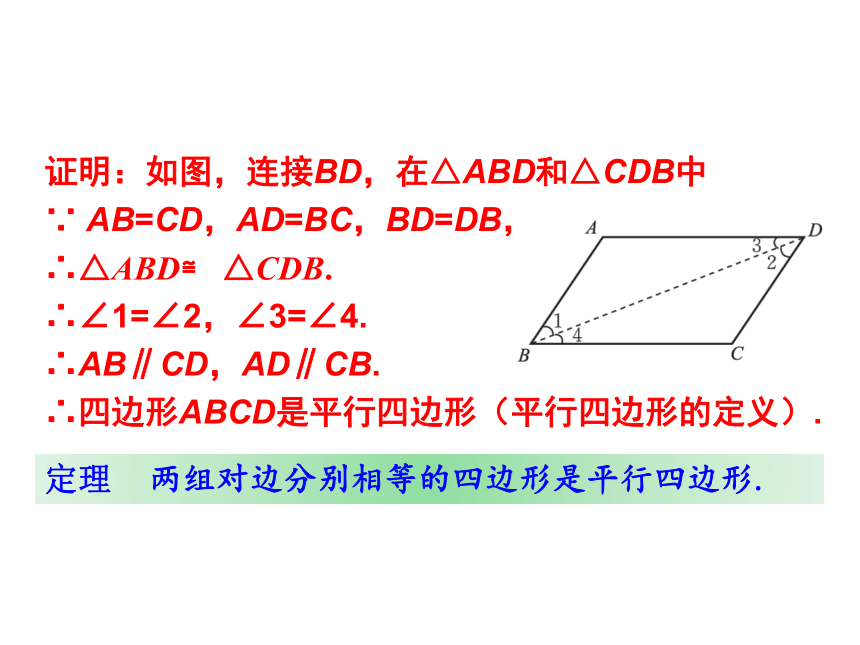
证明:如图,连接BD,在△ABD和△CDB中
∵
AB=CD,AD=BC,BD=DB,
∴△ABD≌
△CDB.
∴∠1=∠2,∠3=∠4.
∴AB∥CD,AD∥CB.
∴四边形ABCD是平行四边形(平行四边形的定义).
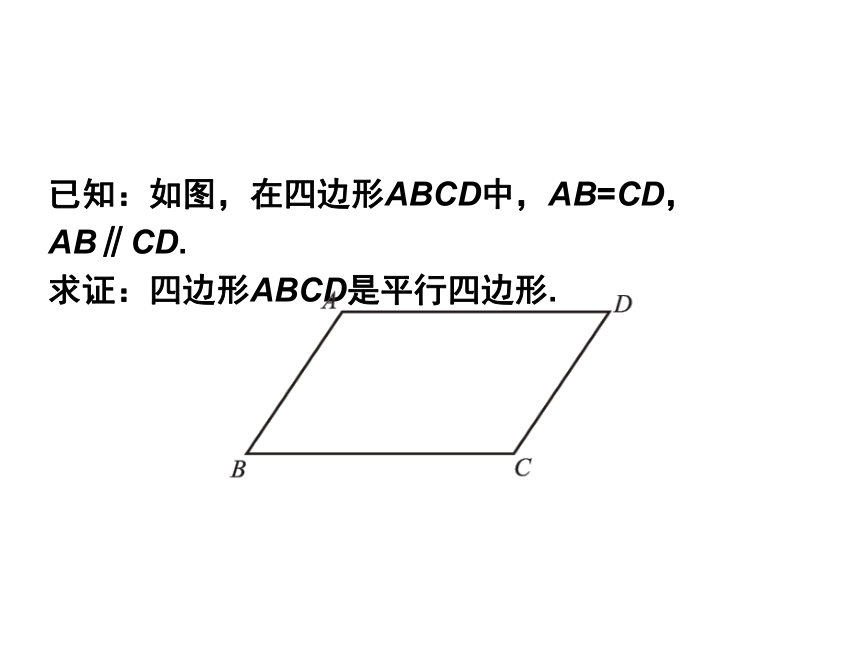
已知:如图,在四边形ABCD中,AB=CD,AB∥CD.
求证:四边形ABCD是平行四边形.
证明:如图,连接AC.
∵
AB∥CD,
∴∠BAC
=
∠DCA.
又∵AB
=
CD,AC
=
CA,
∴△ABC≌△CDA,
∴BC
=
DA.
∴四边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形).
归纳小结
两组对边分别平行的四边形是平行四边形;
A
B
C
D
O
AD∥BC
AB∥DC
四边形ABCD是平行四边形
两组对边分别相等的四边形是平行四边形;
AD
=
BC
AB
=
DC
四边形ABCD是平行四边形
A
B
C
D
O
一组对边平行且相等的四边形是平行四边形;
AD∥BC
AD
=
BC
四边形ABCD是平行四边形
A
B
C
D
O
例1
已知:如图,在
ABCD中,E,F分别为AD和CB的中点.
求证:四边形BFDE是平行四边形.
证明:∵
四边形ABCD是平行四边形,
∴AD
=
CB(平行四边形的对边相等),
AD∥CB(平行四边形的定义).
∵E,F
分别是AD和CB的中点,
∴ED=
AD,FB=
CB.
∴ED
=
FB,ED∥FB.
∴四边形BFDE是平行四边形(一组对边平行且相等的四边形是平行四边形).
练习
1.
如图,线段AD是线段BC经过平移得到的,分别连接AB,CD,四边形ABCD是平行四边形吗?请说明理由.
2.
如图,AC=BD,AB=CD=EF,CE=DF.图中有哪些互相平行的线段?请说明理由.
随堂练习
1.已知:在平行四边形ABCD中,点
E,F,G,H分别是AB,BC,CD,DA的中点.则下图中有几个平行四边形?
解:9个,分别是四边形ABFH,DCFH,AEGD,BEGC,ABCD,AEOH,DGOH,BEOF,CGOF.
O
2.已知:在四边形ABCD中,AB∥CD,要使四边形ABCD为平行四边形,需添加一个条件是什么?
A
B
C
D
解:AD∥BC或AB=CD
3.
□
ABCD的对角线相交于点O,点E、F、G、H分别是OA、OB、OC、OD的中点。四边形EFGH是平行四边形吗?为什么?
答:四边形EFGH是平行四边形.
理由是:
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
又∵点E,F,G,H分别是OA,OB,OC,OD的中点,
∴EF=1/2AB,EF∥AB.
GH=1/2CD,GH∥CD.
∴EF∥GH,EF=GH.
∴四边形EFGH是平行四边形.
课堂小结
平行四边形的判定方法:
1.完成课本P142-143
习题6.3,
2.完成练习册本课时的习题.
课后作业
平行四边形的判定(1)
北师版·八年级数学下册
2
平行四边形的判定
复习回顾
1.什么是平行四边形?
两组对边分别平行的四边形叫做平行四边形.
A
B
C
D
2.我们学行四边形的哪些性质?
平行四边形的两组对边分别相等;
平行四边形的两组对角分别相等;
边
∵四边形ABCD是平行四边形
∴AB=CD,AD=BC
.
角
∵四边形ABCD是平行四边形
∴∠A=∠C,∠D=∠B
.
平行四边形的对角线互相平分.
对角线
∵四边形ABCD是平行四边形
∴OA=OC,OB=OD
.
A
B
C
D
O
推进新课
平行四边形的两组对边分别相等;
平行四边形的两组对角分别相等;
平行四边形的对角线互相平分.
讨论
我们已经学行四边形的这些性质,那么它们的逆命题各是什么呢?
两组对角分别相等的四边形是平行四边形;
对角线互相平分的四边形是平行四边形.
两组对边分别相等的四边形是平行四边形;
思考
我们得到的这些逆命题都成立吗?我们一起探讨一下吧!
已知:如图,在四边形ABCD中,AB=CD,AD=BC.
求证:四边形ABCD是平行四边形.
证明:如图,连接BD,在△ABD和△CDB中
∵
AB=CD,AD=BC,BD=DB,
∴△ABD≌
△CDB.
∴∠1=∠2,∠3=∠4.
∴AB∥CD,AD∥CB.
∴四边形ABCD是平行四边形(平行四边形的定义).
已知:如图,在四边形ABCD中,AB=CD,AB∥CD.
求证:四边形ABCD是平行四边形.
证明:如图,连接AC.
∵
AB∥CD,
∴∠BAC
=
∠DCA.
又∵AB
=
CD,AC
=
CA,
∴△ABC≌△CDA,
∴BC
=
DA.
∴四边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形).
归纳小结
两组对边分别平行的四边形是平行四边形;
A
B
C
D
O
AD∥BC
AB∥DC
四边形ABCD是平行四边形
两组对边分别相等的四边形是平行四边形;
AD
=
BC
AB
=
DC
四边形ABCD是平行四边形
A
B
C
D
O
一组对边平行且相等的四边形是平行四边形;
AD∥BC
AD
=
BC
四边形ABCD是平行四边形
A
B
C
D
O
例1
已知:如图,在
ABCD中,E,F分别为AD和CB的中点.
求证:四边形BFDE是平行四边形.
证明:∵
四边形ABCD是平行四边形,
∴AD
=
CB(平行四边形的对边相等),
AD∥CB(平行四边形的定义).
∵E,F
分别是AD和CB的中点,
∴ED=
AD,FB=
CB.
∴ED
=
FB,ED∥FB.
∴四边形BFDE是平行四边形(一组对边平行且相等的四边形是平行四边形).
练习
1.
如图,线段AD是线段BC经过平移得到的,分别连接AB,CD,四边形ABCD是平行四边形吗?请说明理由.
2.
如图,AC=BD,AB=CD=EF,CE=DF.图中有哪些互相平行的线段?请说明理由.
随堂练习
1.已知:在平行四边形ABCD中,点
E,F,G,H分别是AB,BC,CD,DA的中点.则下图中有几个平行四边形?
解:9个,分别是四边形ABFH,DCFH,AEGD,BEGC,ABCD,AEOH,DGOH,BEOF,CGOF.
O
2.已知:在四边形ABCD中,AB∥CD,要使四边形ABCD为平行四边形,需添加一个条件是什么?
A
B
C
D
解:AD∥BC或AB=CD
3.
□
ABCD的对角线相交于点O,点E、F、G、H分别是OA、OB、OC、OD的中点。四边形EFGH是平行四边形吗?为什么?
答:四边形EFGH是平行四边形.
理由是:
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
又∵点E,F,G,H分别是OA,OB,OC,OD的中点,
∴EF=1/2AB,EF∥AB.
GH=1/2CD,GH∥CD.
∴EF∥GH,EF=GH.
∴四边形EFGH是平行四边形.
课堂小结
平行四边形的判定方法:
1.完成课本P142-143
习题6.3,
2.完成练习册本课时的习题.
课后作业
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
