北师大版数学八年级下册课件:6.4.多边形的内角和与外角和(共28张PPT)
文档属性
| 名称 | 北师大版数学八年级下册课件:6.4.多边形的内角和与外角和(共28张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 795.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-17 08:41:43 | ||
图片预览




文档简介
4.多边形的内角和与外角和
北师版·八年级数学下册
新课导入
三角形是如何定义的?
思考
三角形是由同一平面内不在同一直线上的三条线段‘首尾’顺次连接所组成的封闭图形.
仿照三角形定义,你能学着给四边形.五边形……n边形下定义吗?
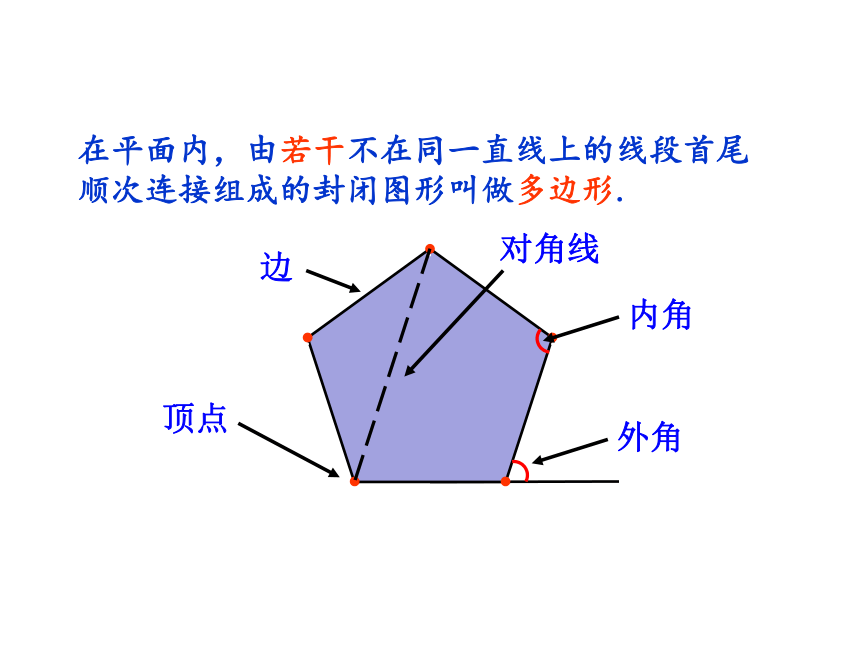
在平面内,由若干不在同一直线上的线段首尾顺次连接组成的封闭图形叫做多边形.
.
.
.
.
.
顶点
对角线
边
内角
外角
推进新课
(1)上图中广场中心的边缘是一个五边形,你能设法求出它的五个内角的和吗?与同伴交流.
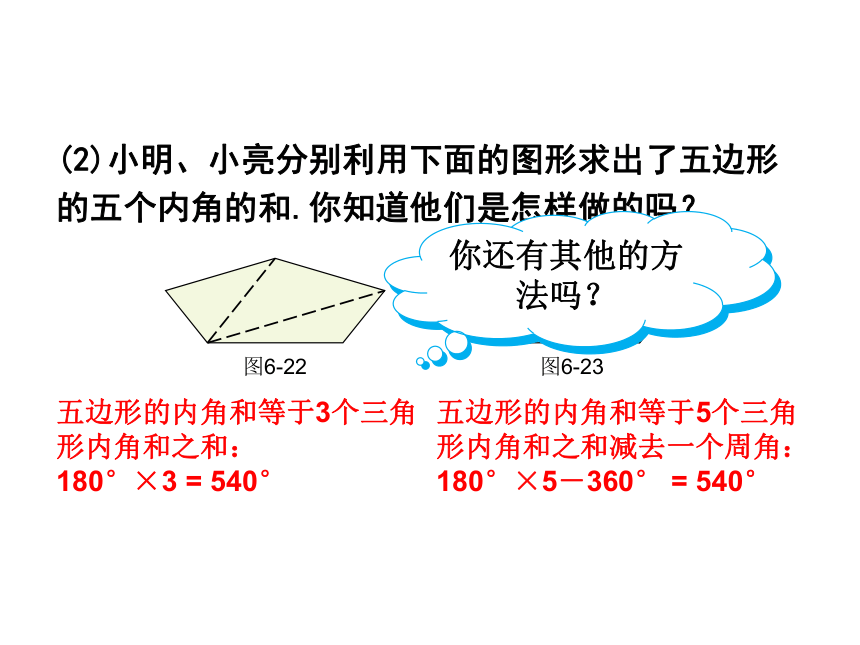
(2)小明、小亮分别利用下面的图形求出了五边形的五个内角的和.你知道他们是怎样做的吗?
图6-22
图6-23
五边形的内角和等于3个三角形内角和之和:
180°×3 = 540°
五边形的内角和等于5个三角形内角和之和减去一个周角:
180°×5-360° = 540°
你还有其他的方法吗?
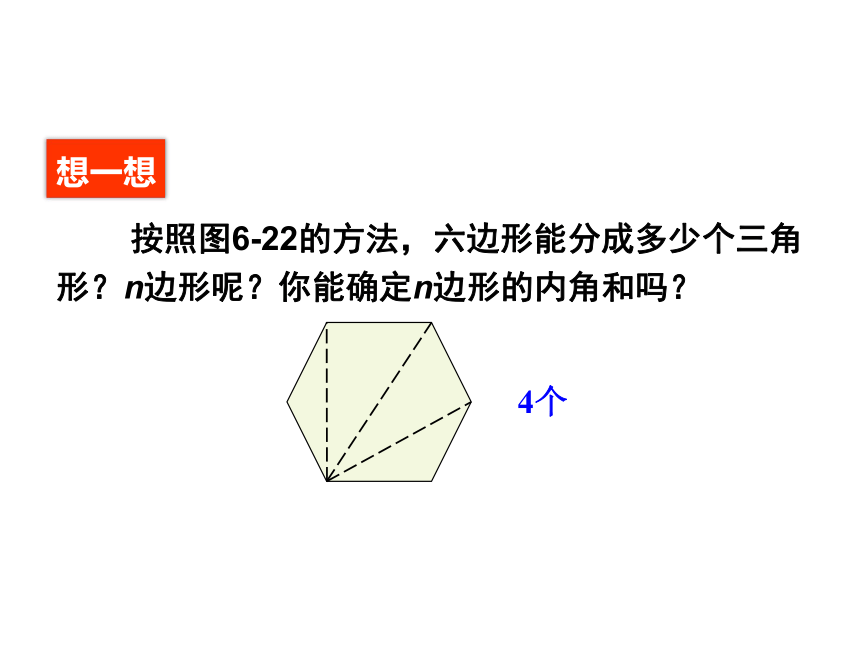
按照图6-22的方法,六边形能分成多少个三角形?n边形呢?你能确定n边形的内角和吗?
想一想
4个
……
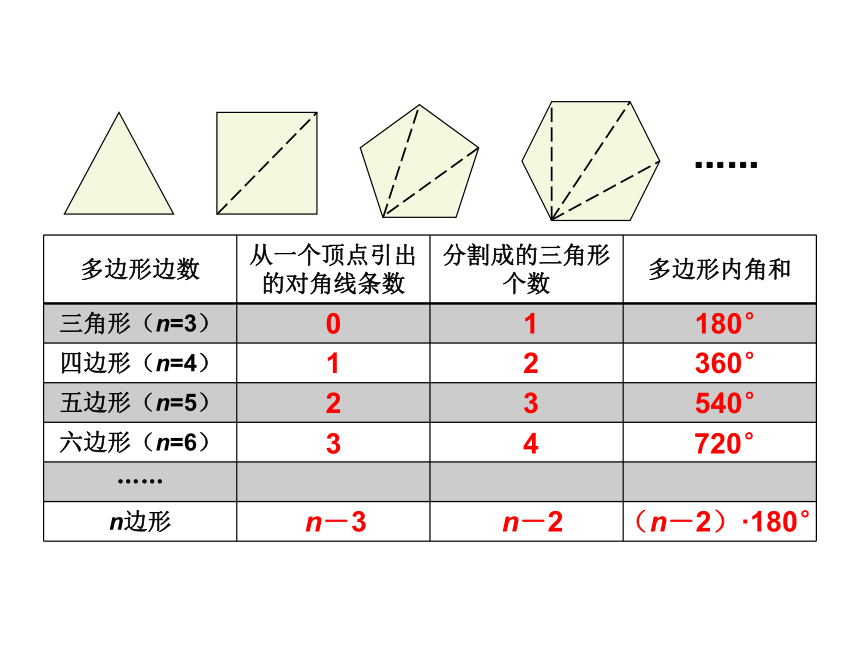
多边形边数
从一个顶点引出的对角线条数
分割成的三角形个数
多边形内角和
三角形(n=3)
四边形(n=4)
五边形(n=5)
六边形(n=6)
……
n边形
0
1
180°
1
2
360°
2
3
540°
3
4
720°
n-3
n-2
(n-2)·180°
归纳小结
定理 n边形的内角和等于(n-2)·180°(n是大于或等于3的自然数).
按照图6-22的方法再试一试.
例1 如图,在四边形ABCD中,∠A+∠C=180°.
∠B与∠D有怎样的关系?
解:∵∠A+∠B+∠C+∠D
=(4-2)×180°=360°,
∴ ∠B+∠D
=360°-( ∠A+∠C )
=360°-180°=180°.
观察图中的多边形,它们的边、角有什么特点?
想一想
正多边形定义:在平面内,每个内角都相等、每条边也都相等的多边形叫做正多边形。
1.一个多边形的边都相等,它的内角一定都相等吗?
2.一个多边形的内角都相等,它的边一定都相等吗?
思考
1. 正三角形、正四边形、正五边形、正六边形、正八边形的内角分别是多少度?
练习
60°
90°
108°
120°
135°
正n边形呢?
2. 小彬求出一个正多边形的一个内角为145°.他的计算正确吗?如果正确,他求的是正几边形的内角?如果不正确,请说明理由.
如图,小刚沿一个五边形广场周围的小路,按逆时针方向跑步.
(1)小刚每从一条小路转到下一条小路时,跑步方向改变的角是哪个角?在图上标出这些角.
(2)他每跑完一圈,跑步方向改变的角一共有几个?它们的和是多少?
小刚是这样思考的:如图,跑步方向改变的角分别是∠1,∠2,∠3,∠4,∠5.
∵∠1+∠EAB=180°,∠2+∠ABC=180°,
∠3+∠BCD=180°,∠4+∠CDE=180°,
∠5+∠DEA=180°,
∴∠1+∠EAB+∠2+∠ABC+∠3+∠BCD+
∠4+∠CDE+∠5+∠DEA=900°
∵五边形的内角和为(5-2)×180°=540°,
即∠EAB+∠ABC+∠BCD+∠CDE+∠DEA=540°
∴∠1+∠2+∠3+∠4+∠5=360°
1 .如果广场的形状是六边形,那么还有类似的结论吗?
问题延伸
2 .如果广场的形状是八边形呢?
6×180°-(6-2)×180°=360°
8×180°-(8-2)×180°=360°
1.多边形内角的一边与另一边的反向延长线所组成的角叫做这个多边形的外角.
2.在每个顶点处取这个多边形的一个外角,它们的和叫做这个多边形的外角和.
归纳小结
定理 多边形的外角和都等于360°.
1 . 还有什么方法可以推导出多边形外角和公式?
思考
2 . 利用多边形外角和的结论,能否推导出多边形内角和的结论?
例2 一个多边形的内角和等于它的外角和的3倍,它是几边形?
解:设这个多边形是n边形,则它的内角和是(n-2)·180°,外角和等于360°.根据题意,得(n-2)·180°=3×360°.
解得n=8.
所以,这个多边形是八边形.
一个多边形的内角和是外角和的2倍,它是几边形?如果这个多边形的每个内角都相等,那么每个内角等于多少度?
练习
随堂练习
1.四边形ABCD中,如果∠A+∠C+∠D=280°,则∠B的度数是( )
A.80° B.90° C.170° D.20°
2.一个多边形的内角和等于1080°,这个多边形的边数是( )
A.9 B.8 C.7 D.6
A
B
3.内角和等于外角和2倍的多边形是( )
A.五边形 B.六边形
C.七边形 D.八边形
4.六边形的内角和等于______度.
5.正十边形的每一个内角的度数等于______,每一个外角的度数等于______.
B
720
144°
36°
6.已知:如图,在四边形ABCD中,∠A=∠C=
90°,BE平分∠ABC,DF平分∠ADC.BE与DF有怎样的位置关系?为什么?
解:BE∥DF.
理由:∵∠A=∠C=90°,
∴∠A+∠C=180°.
∴∠ABC+∠ADC=360°-180°=180°.
∵∠ABE=1/2∠ABC,∠ADF=1/2∠ADC,
∴∠ABE+∠ADF= 1/2(∠ABC+∠ADC)=1/2 ×180°=90°.
又∵∠ABE+∠AEB=90°,
∴∠AEB=∠ADF,
∴BE∥DF(同位角相等,两直线平行).
7. 如图,以五边形的每个顶点为圆心,以1为半径画圆,求圆与五边形重合的面积.
解:(5-2)×180°÷360°×12×π=1.5π.
课堂小结
谈谈你在这节课中,有什么收获?
1.完成课本P155习题6.7;P157习题6.8,
2.完成练习册本课时的习题.
课后作业
北师版·八年级数学下册
新课导入
三角形是如何定义的?
思考
三角形是由同一平面内不在同一直线上的三条线段‘首尾’顺次连接所组成的封闭图形.
仿照三角形定义,你能学着给四边形.五边形……n边形下定义吗?
在平面内,由若干不在同一直线上的线段首尾顺次连接组成的封闭图形叫做多边形.
.
.
.
.
.
顶点
对角线
边
内角
外角
推进新课
(1)上图中广场中心的边缘是一个五边形,你能设法求出它的五个内角的和吗?与同伴交流.
(2)小明、小亮分别利用下面的图形求出了五边形的五个内角的和.你知道他们是怎样做的吗?
图6-22
图6-23
五边形的内角和等于3个三角形内角和之和:
180°×3 = 540°
五边形的内角和等于5个三角形内角和之和减去一个周角:
180°×5-360° = 540°
你还有其他的方法吗?
按照图6-22的方法,六边形能分成多少个三角形?n边形呢?你能确定n边形的内角和吗?
想一想
4个
……
多边形边数
从一个顶点引出的对角线条数
分割成的三角形个数
多边形内角和
三角形(n=3)
四边形(n=4)
五边形(n=5)
六边形(n=6)
……
n边形
0
1
180°
1
2
360°
2
3
540°
3
4
720°
n-3
n-2
(n-2)·180°
归纳小结
定理 n边形的内角和等于(n-2)·180°(n是大于或等于3的自然数).
按照图6-22的方法再试一试.
例1 如图,在四边形ABCD中,∠A+∠C=180°.
∠B与∠D有怎样的关系?
解:∵∠A+∠B+∠C+∠D
=(4-2)×180°=360°,
∴ ∠B+∠D
=360°-( ∠A+∠C )
=360°-180°=180°.
观察图中的多边形,它们的边、角有什么特点?
想一想
正多边形定义:在平面内,每个内角都相等、每条边也都相等的多边形叫做正多边形。
1.一个多边形的边都相等,它的内角一定都相等吗?
2.一个多边形的内角都相等,它的边一定都相等吗?
思考
1. 正三角形、正四边形、正五边形、正六边形、正八边形的内角分别是多少度?
练习
60°
90°
108°
120°
135°
正n边形呢?
2. 小彬求出一个正多边形的一个内角为145°.他的计算正确吗?如果正确,他求的是正几边形的内角?如果不正确,请说明理由.
如图,小刚沿一个五边形广场周围的小路,按逆时针方向跑步.
(1)小刚每从一条小路转到下一条小路时,跑步方向改变的角是哪个角?在图上标出这些角.
(2)他每跑完一圈,跑步方向改变的角一共有几个?它们的和是多少?
小刚是这样思考的:如图,跑步方向改变的角分别是∠1,∠2,∠3,∠4,∠5.
∵∠1+∠EAB=180°,∠2+∠ABC=180°,
∠3+∠BCD=180°,∠4+∠CDE=180°,
∠5+∠DEA=180°,
∴∠1+∠EAB+∠2+∠ABC+∠3+∠BCD+
∠4+∠CDE+∠5+∠DEA=900°
∵五边形的内角和为(5-2)×180°=540°,
即∠EAB+∠ABC+∠BCD+∠CDE+∠DEA=540°
∴∠1+∠2+∠3+∠4+∠5=360°
1 .如果广场的形状是六边形,那么还有类似的结论吗?
问题延伸
2 .如果广场的形状是八边形呢?
6×180°-(6-2)×180°=360°
8×180°-(8-2)×180°=360°
1.多边形内角的一边与另一边的反向延长线所组成的角叫做这个多边形的外角.
2.在每个顶点处取这个多边形的一个外角,它们的和叫做这个多边形的外角和.
归纳小结
定理 多边形的外角和都等于360°.
1 . 还有什么方法可以推导出多边形外角和公式?
思考
2 . 利用多边形外角和的结论,能否推导出多边形内角和的结论?
例2 一个多边形的内角和等于它的外角和的3倍,它是几边形?
解:设这个多边形是n边形,则它的内角和是(n-2)·180°,外角和等于360°.根据题意,得(n-2)·180°=3×360°.
解得n=8.
所以,这个多边形是八边形.
一个多边形的内角和是外角和的2倍,它是几边形?如果这个多边形的每个内角都相等,那么每个内角等于多少度?
练习
随堂练习
1.四边形ABCD中,如果∠A+∠C+∠D=280°,则∠B的度数是( )
A.80° B.90° C.170° D.20°
2.一个多边形的内角和等于1080°,这个多边形的边数是( )
A.9 B.8 C.7 D.6
A
B
3.内角和等于外角和2倍的多边形是( )
A.五边形 B.六边形
C.七边形 D.八边形
4.六边形的内角和等于______度.
5.正十边形的每一个内角的度数等于______,每一个外角的度数等于______.
B
720
144°
36°
6.已知:如图,在四边形ABCD中,∠A=∠C=
90°,BE平分∠ABC,DF平分∠ADC.BE与DF有怎样的位置关系?为什么?
解:BE∥DF.
理由:∵∠A=∠C=90°,
∴∠A+∠C=180°.
∴∠ABC+∠ADC=360°-180°=180°.
∵∠ABE=1/2∠ABC,∠ADF=1/2∠ADC,
∴∠ABE+∠ADF= 1/2(∠ABC+∠ADC)=1/2 ×180°=90°.
又∵∠ABE+∠AEB=90°,
∴∠AEB=∠ADF,
∴BE∥DF(同位角相等,两直线平行).
7. 如图,以五边形的每个顶点为圆心,以1为半径画圆,求圆与五边形重合的面积.
解:(5-2)×180°÷360°×12×π=1.5π.
课堂小结
谈谈你在这节课中,有什么收获?
1.完成课本P155习题6.7;P157习题6.8,
2.完成练习册本课时的习题.
课后作业
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
