北师大版数学七年级下册第二章 相交线与平行线 复习课件 (共28张PPT)
文档属性
| 名称 | 北师大版数学七年级下册第二章 相交线与平行线 复习课件 (共28张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 764.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-17 00:00:00 | ||
图片预览



文档简介
章末复习
北师大版七年级数学下册
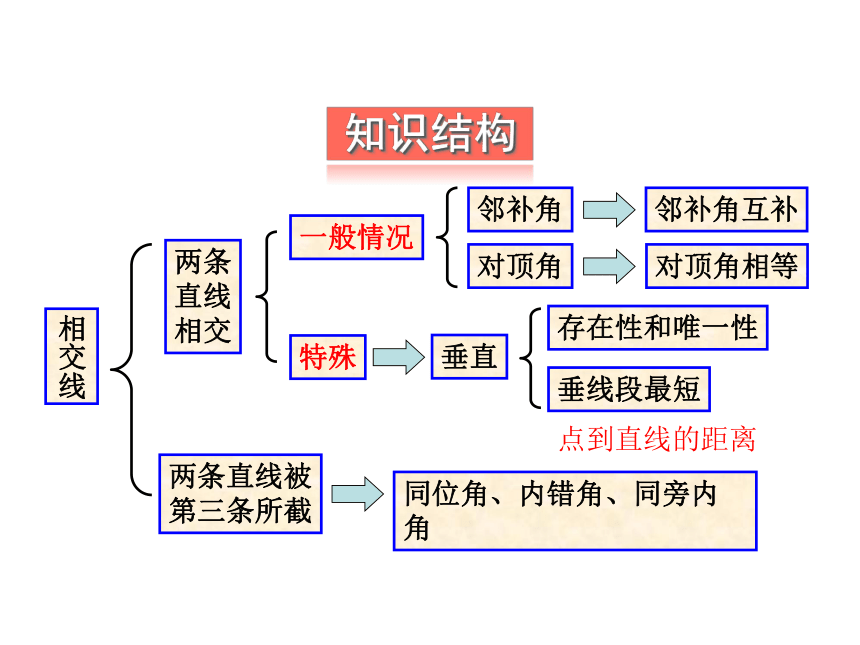
知识结构
相交线
两条直线相交
一般情况
邻补角
对顶角
邻补角互补
对顶角相等
特殊
垂直
存在性和唯一性
垂线段最短
两条直线被
第三条所截
同位角、内错角、同旁内角
点到直线的距离
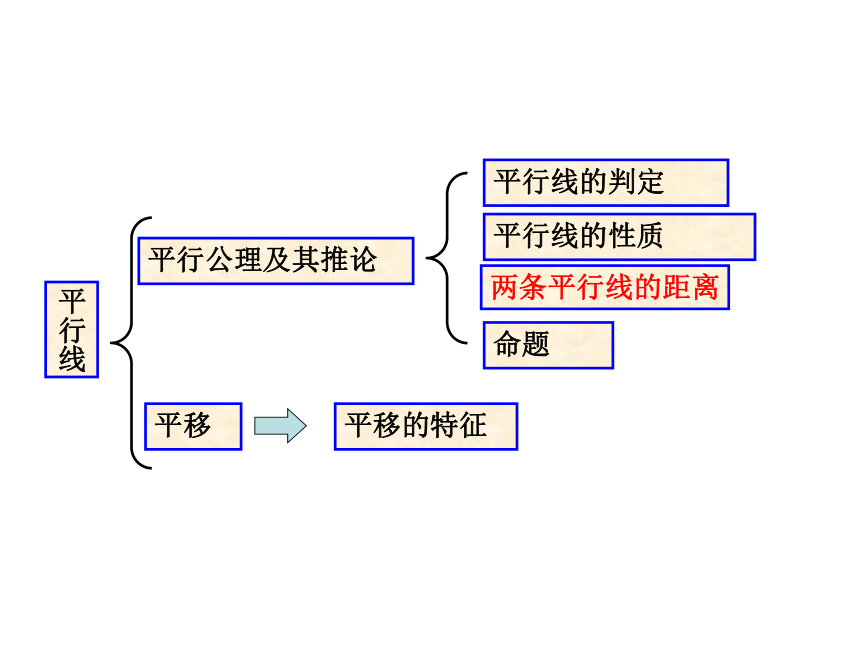
平行线
平行公理及其推论
平行线的判定
平行线的性质
两条平行线的距离
命题
平移
平移的特征
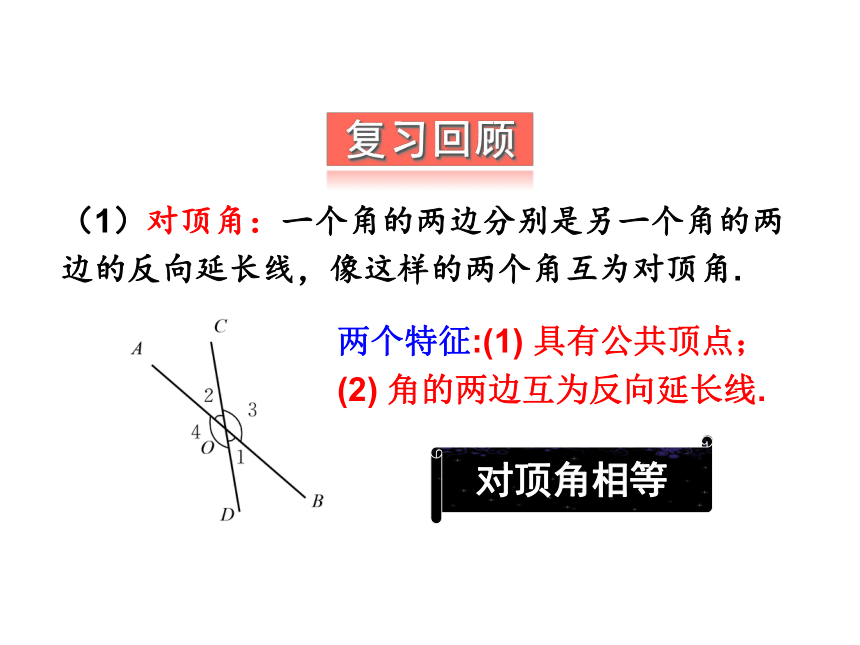
复习回顾
(1)对顶角:一个角的两边分别是另一个角的两边的反向延长线,像这样的两个角互为对顶角.
两个特征:(1) 具有公共顶点;
(2) 角的两边互为反向延长线.
对顶角相等
(2)补角:如果两个角的和是180°,那么称这两个角互为补角.
(3)余角:如果两个角的和是90°,那么称这两个角互为余角.
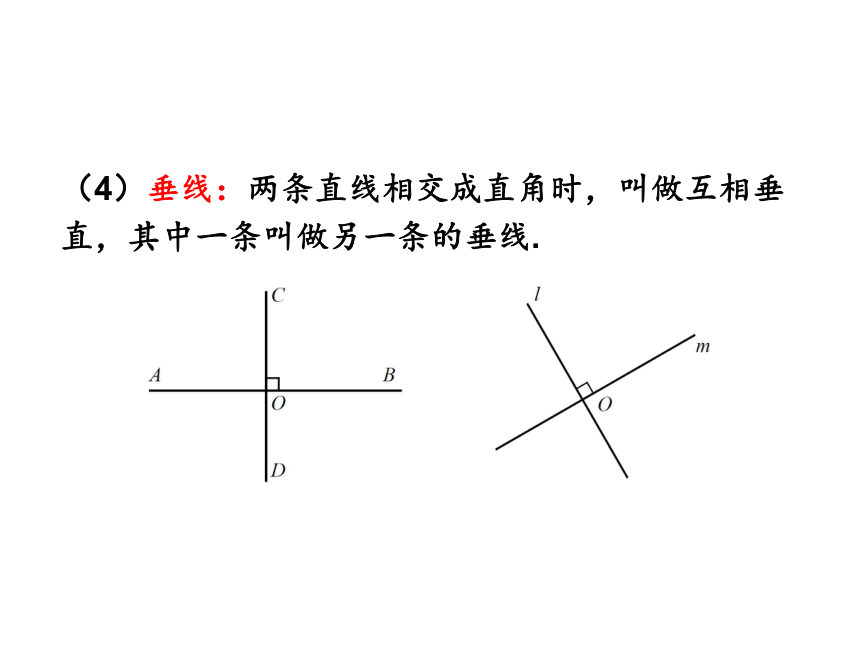
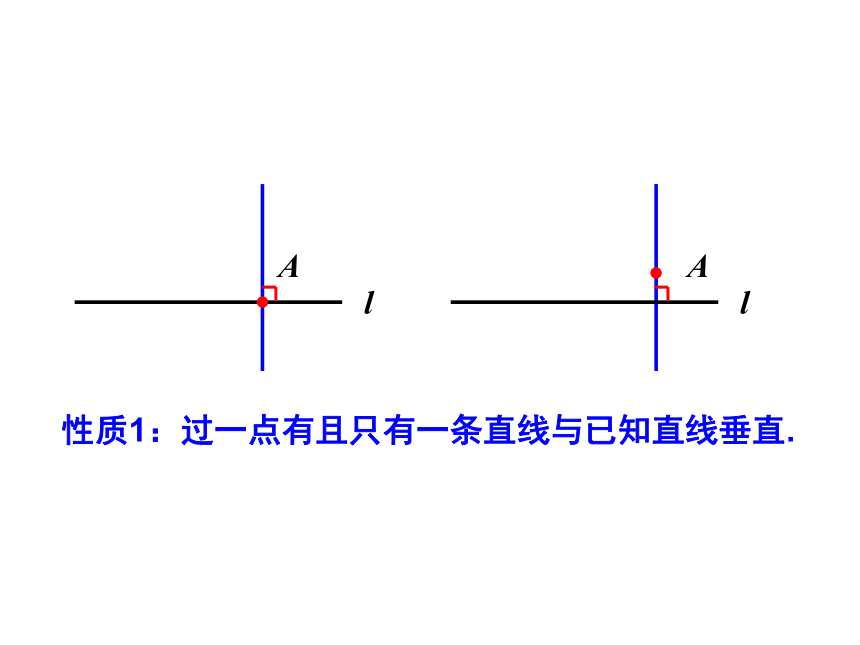
(4)垂线:两条直线相交成直角时,叫做互相垂直,其中一条叫做另一条的垂线.
l
A
l
A
性质1:过一点有且只有一条直线与已知直线垂直.
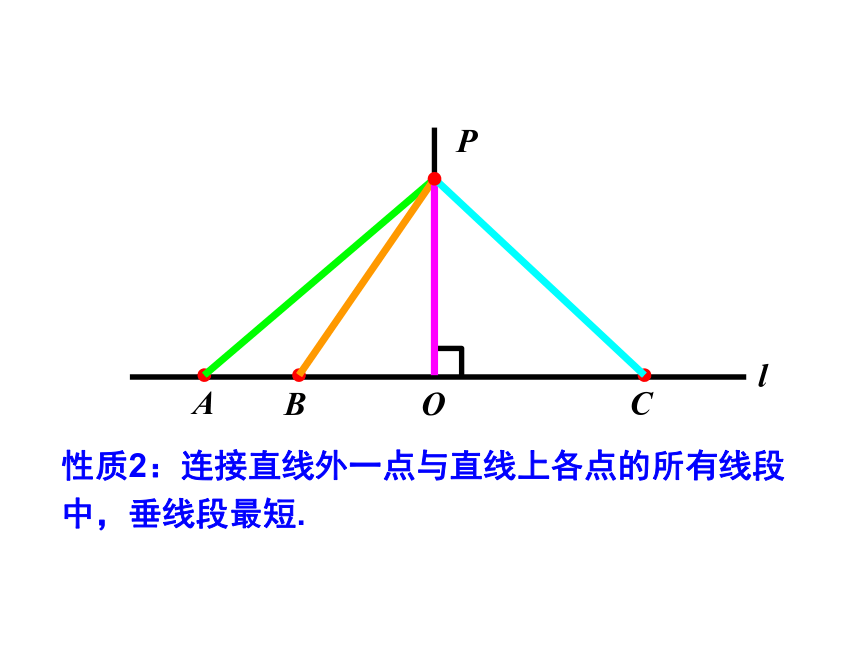
性质2:连接直线外一点与直线上各点的所有线段中,垂线段最短.
l
O
C
B
A
P
(5)平行线:在同一平面内,不相交的两条直线叫做平行线.
b
a
c
1
2
3
4
5
6
7
8
∠1与∠5像这样具有相同位置关系的一对角叫做同位角.
∠4与∠6像这样的一对角叫做内错角.
∠4与∠5像这样的一对角叫做同旁内角.
过直线外一点有且只有一条直线与这条直线平行.
平行于同一条直线的两条直线平行.
A
B
P
a
b
c
A
B
C
D
4
1
3
2
(6)平行线的性质:
性质1:两直线平行,同位角相等.
性质2:两直线平行,内错角相等.
性质3:两直线平行,同旁内角互补.
(7)平行线的判定:
判定1:同位角相等,两直线平行.
判定2:内错角相等,两直线平行.
判定3:同旁内角互补,两直线平行.
A
B
C
D
4
1
3
2
典例精析
例1 下列说法错误的是( )
A.同位角不一定相等
B.内错角都相等
C.同旁内角可能相等
D.同旁内角互补则两直线平行
B
例2 同一平面内,下列说法:①过两点有且只有一条直线;②两直线不平行,则一定相交;③过一点有且只有一条直线与已知直线垂直;④过一点有且仅有一条直线与已知直线平行,其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
D
例3 如图,下列条件能证明AD∥BC的是( )
A.∠A=∠C B.∠B=∠D
C.∠B=∠C D.∠A+∠B=180°
D
例4 如图,
(1)∵∠ABD=∠BDC(已知),∴ ___∥ ___ ( );
(2)∵∠DBC=∠ADB(已知),∴ ___∥ ___ ( );
(3)∵∠CBE=∠DCB(已知),∴ ___ ∥___ ( );
(4)∵∠CBE=∠A,(已知),∴ ___ ∥ ___ ( );
(5)∵∠A+∠ADC=180°(已知),∴ ___ ∥ ___( );
(6)∵∠A+∠ABC=180°(已知),∴ ___ ∥ ___( ).
解:(1)CD∥AB,内错角相等,两直线平行;
(2)AD∥BC,内错角相等,两直线平行;
(3)CD∥BE,内错角相等,两直线平行;
(4)AD∥BC,同位角相等,两直线平行;
(5)AB∥CD,同旁内角互补,两直线平行;
(6)AD∥BC,同旁内角互补,两直线平行.
例5 如图,∠1=∠2,AC平分∠DAB,DC∥AB吗?为什么?
解:DC∥AB.理由:
因为由AC平分∠DAB,故∠1=∠CAB,又∠1=∠2,所以∠2=∠CAB.因而AB∥CD(内错角相等,两直线平行).
例6 如图,∠ABC=∠ADC,BF和DE分别平分∠ABC和∠ADC,∠1=∠2,DE∥FB吗?为什么?
解:DE∥FB.理由:
因为∠ADC=∠ABC,且∠2=∠ADE,
∠CBF=∠ABF,故∠2=∠ABF.
又∠2=∠1,因此∠1=∠ABF,
所以DE∥BF(同位角相等,两直线平行).
例7 如图,AB∥CD,∠BAE=30°,∠ECD=60°,那么∠AEC度数为多少?
解:如图,过E作EF∥AB,
则∠1=∠A=30°;因为AB∥CD,
所以EF∥CD(如果两条直线都与第三条直线平行,那么这两条直线也互相平行),
所以∠2=∠C=60°,
那么∠AEC=∠1+∠2=30°+60°=90°.
随堂练习
1.如图,BC⊥AC,CB=8cm,AC=6cm,AB=10cm,那么点A到BC的距离是______,点B到AC的距离是______ ,A、B两点的距离是______ ,点C到AB的距离是______.
6cm
8cm
10cm
4.8cm
2.设a、b、c为平面上三条不同直线,
若a//b,b//c,则a与c的位置关系是________;
若a⊥b,b⊥c,则a与c的位置关系是________;
若a//b,b⊥c,则a与c的位置关系是________.
平行
平行
垂直
3.下列图形中,由AB∥CD,能得到∠1=∠2的是( )
B
4. 如图,直线L1∥L2,则∠α为( )
A.150° B.140° C.130° D.120°
D
5.(1)如图,已知∠1=∠2,试判断a、b的位置关系.(2)直线a//b,∠1=∠2吗?为什么?
解:(1)a∥b.理由:
因为∠1=∠2,又因为∠2=∠3(对顶角相等),所以∠1=∠3,所以a∥b(同位角相等两直线平行).
(2)∠1=∠2.理由:因为a∥b,所以∠1=∠3(两直线平行,同位角相等).又因为∠2=∠3(对顶角相等).所以∠1=∠2.
6.如图,已知△ABC,AD⊥BC于D,E为AB上一点,EF⊥BC于F,DG//BA交CA于G.∠1与∠2相等吗?为什么?
解:∠1=∠2.理由:
因为AD⊥BC,FE⊥BC,
所以∠EFB=∠ADB=90°,所以EF//AD,
所以∠2=∠3,
因为DG//BA,所以∠3=∠1,所以∠1=∠2.
课堂小结
谈谈你在这节课中,有什么收获?
课后作业
1.完成课本P58-60 复习题;
2.完成练习册本课时的习题.
北师大版七年级数学下册
知识结构
相交线
两条直线相交
一般情况
邻补角
对顶角
邻补角互补
对顶角相等
特殊
垂直
存在性和唯一性
垂线段最短
两条直线被
第三条所截
同位角、内错角、同旁内角
点到直线的距离
平行线
平行公理及其推论
平行线的判定
平行线的性质
两条平行线的距离
命题
平移
平移的特征
复习回顾
(1)对顶角:一个角的两边分别是另一个角的两边的反向延长线,像这样的两个角互为对顶角.
两个特征:(1) 具有公共顶点;
(2) 角的两边互为反向延长线.
对顶角相等
(2)补角:如果两个角的和是180°,那么称这两个角互为补角.
(3)余角:如果两个角的和是90°,那么称这两个角互为余角.
(4)垂线:两条直线相交成直角时,叫做互相垂直,其中一条叫做另一条的垂线.
l
A
l
A
性质1:过一点有且只有一条直线与已知直线垂直.
性质2:连接直线外一点与直线上各点的所有线段中,垂线段最短.
l
O
C
B
A
P
(5)平行线:在同一平面内,不相交的两条直线叫做平行线.
b
a
c
1
2
3
4
5
6
7
8
∠1与∠5像这样具有相同位置关系的一对角叫做同位角.
∠4与∠6像这样的一对角叫做内错角.
∠4与∠5像这样的一对角叫做同旁内角.
过直线外一点有且只有一条直线与这条直线平行.
平行于同一条直线的两条直线平行.
A
B
P
a
b
c
A
B
C
D
4
1
3
2
(6)平行线的性质:
性质1:两直线平行,同位角相等.
性质2:两直线平行,内错角相等.
性质3:两直线平行,同旁内角互补.
(7)平行线的判定:
判定1:同位角相等,两直线平行.
判定2:内错角相等,两直线平行.
判定3:同旁内角互补,两直线平行.
A
B
C
D
4
1
3
2
典例精析
例1 下列说法错误的是( )
A.同位角不一定相等
B.内错角都相等
C.同旁内角可能相等
D.同旁内角互补则两直线平行
B
例2 同一平面内,下列说法:①过两点有且只有一条直线;②两直线不平行,则一定相交;③过一点有且只有一条直线与已知直线垂直;④过一点有且仅有一条直线与已知直线平行,其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
D
例3 如图,下列条件能证明AD∥BC的是( )
A.∠A=∠C B.∠B=∠D
C.∠B=∠C D.∠A+∠B=180°
D
例4 如图,
(1)∵∠ABD=∠BDC(已知),∴ ___∥ ___ ( );
(2)∵∠DBC=∠ADB(已知),∴ ___∥ ___ ( );
(3)∵∠CBE=∠DCB(已知),∴ ___ ∥___ ( );
(4)∵∠CBE=∠A,(已知),∴ ___ ∥ ___ ( );
(5)∵∠A+∠ADC=180°(已知),∴ ___ ∥ ___( );
(6)∵∠A+∠ABC=180°(已知),∴ ___ ∥ ___( ).
解:(1)CD∥AB,内错角相等,两直线平行;
(2)AD∥BC,内错角相等,两直线平行;
(3)CD∥BE,内错角相等,两直线平行;
(4)AD∥BC,同位角相等,两直线平行;
(5)AB∥CD,同旁内角互补,两直线平行;
(6)AD∥BC,同旁内角互补,两直线平行.
例5 如图,∠1=∠2,AC平分∠DAB,DC∥AB吗?为什么?
解:DC∥AB.理由:
因为由AC平分∠DAB,故∠1=∠CAB,又∠1=∠2,所以∠2=∠CAB.因而AB∥CD(内错角相等,两直线平行).
例6 如图,∠ABC=∠ADC,BF和DE分别平分∠ABC和∠ADC,∠1=∠2,DE∥FB吗?为什么?
解:DE∥FB.理由:
因为∠ADC=∠ABC,且∠2=∠ADE,
∠CBF=∠ABF,故∠2=∠ABF.
又∠2=∠1,因此∠1=∠ABF,
所以DE∥BF(同位角相等,两直线平行).
例7 如图,AB∥CD,∠BAE=30°,∠ECD=60°,那么∠AEC度数为多少?
解:如图,过E作EF∥AB,
则∠1=∠A=30°;因为AB∥CD,
所以EF∥CD(如果两条直线都与第三条直线平行,那么这两条直线也互相平行),
所以∠2=∠C=60°,
那么∠AEC=∠1+∠2=30°+60°=90°.
随堂练习
1.如图,BC⊥AC,CB=8cm,AC=6cm,AB=10cm,那么点A到BC的距离是______,点B到AC的距离是______ ,A、B两点的距离是______ ,点C到AB的距离是______.
6cm
8cm
10cm
4.8cm
2.设a、b、c为平面上三条不同直线,
若a//b,b//c,则a与c的位置关系是________;
若a⊥b,b⊥c,则a与c的位置关系是________;
若a//b,b⊥c,则a与c的位置关系是________.
平行
平行
垂直
3.下列图形中,由AB∥CD,能得到∠1=∠2的是( )
B
4. 如图,直线L1∥L2,则∠α为( )
A.150° B.140° C.130° D.120°
D
5.(1)如图,已知∠1=∠2,试判断a、b的位置关系.(2)直线a//b,∠1=∠2吗?为什么?
解:(1)a∥b.理由:
因为∠1=∠2,又因为∠2=∠3(对顶角相等),所以∠1=∠3,所以a∥b(同位角相等两直线平行).
(2)∠1=∠2.理由:因为a∥b,所以∠1=∠3(两直线平行,同位角相等).又因为∠2=∠3(对顶角相等).所以∠1=∠2.
6.如图,已知△ABC,AD⊥BC于D,E为AB上一点,EF⊥BC于F,DG//BA交CA于G.∠1与∠2相等吗?为什么?
解:∠1=∠2.理由:
因为AD⊥BC,FE⊥BC,
所以∠EFB=∠ADB=90°,所以EF//AD,
所以∠2=∠3,
因为DG//BA,所以∠3=∠1,所以∠1=∠2.
课堂小结
谈谈你在这节课中,有什么收获?
课后作业
1.完成课本P58-60 复习题;
2.完成练习册本课时的习题.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
