北师大版数学七年级下册课件:2.1.1 对顶角、余角和补角(共23张PPT)
文档属性
| 名称 | 北师大版数学七年级下册课件:2.1.1 对顶角、余角和补角(共23张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-17 12:35:58 | ||
图片预览





文档简介
第1课时 对顶角、余角和补角
1 两条直线的位置关系
情境导入
生活中处处可见道路、房屋、山川、桥梁。在大自然的杰作和人类的创造物中,蕴含着无数的相交线和平行线。我们知道:
在同一平面内,两条直线的位置关系有相交和平行两种.
在同一平面内,不相交的两条直线叫平行线.
探索新知
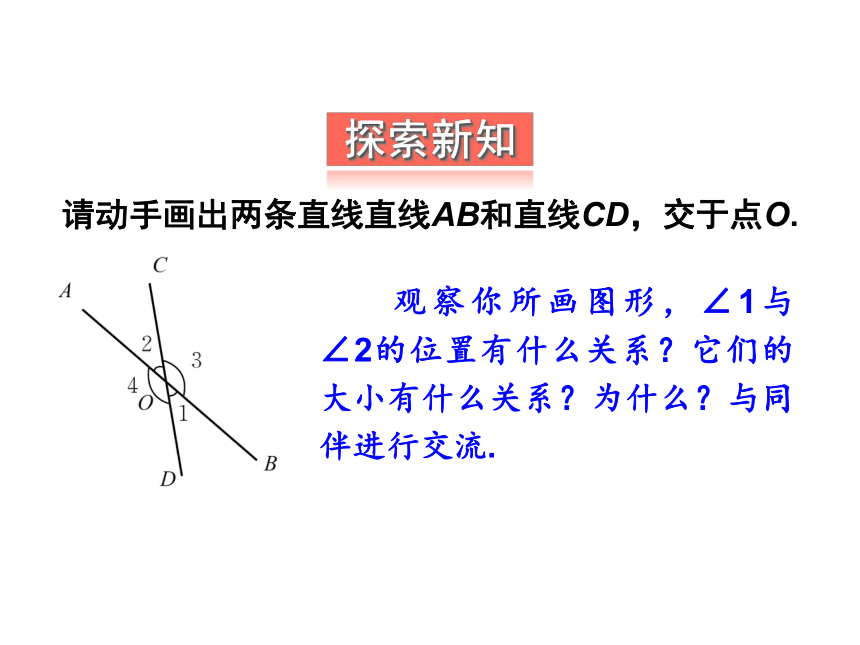
请动手画出两条直线直线AB和直线CD,交于点O.
观察你所画图形,∠1与∠2的位置有什么关系?它们的大小有什么关系?为什么?与同伴进行交流.
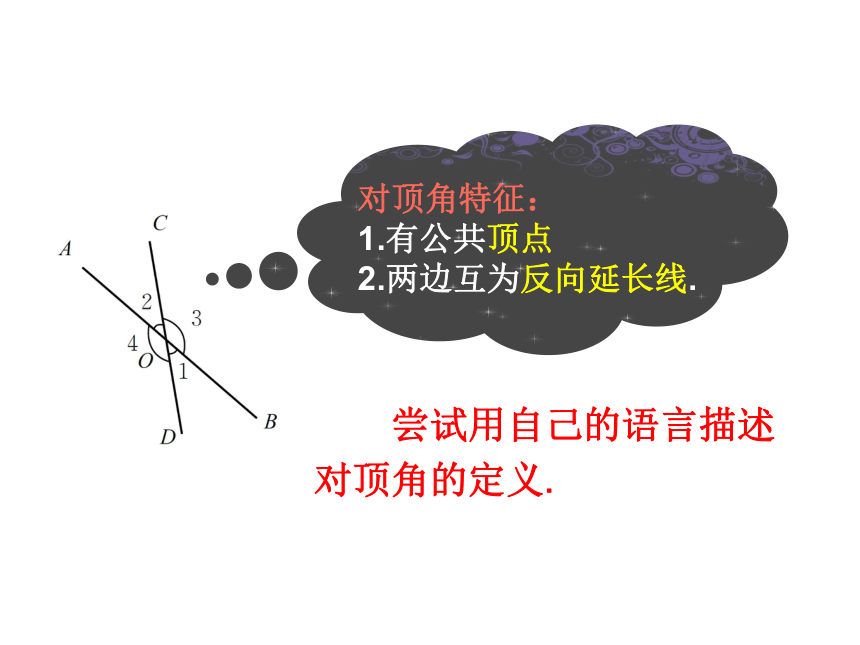
对顶角特征:
1.有公共顶点
2.两边互为反向延长线.
尝试用自己的语言描述对顶角的定义.
归纳总结
直线AB与CD相交于点O,∠1与∠2有公共顶点O,它们的两边互为反向延长线,具有这种位置关系的两个角叫做对顶角.
请你观察图中∠1和∠2这组对顶角,你发现它们的大小有什么关系?
因为∠1+∠3=180°(平角定义)
∠2+∠3=180°(平角定义)
所以∠1=∠2(等量代换)
对顶角相等
对顶角有如下性质:
认一认
(1)下列各图中,∠1与∠2是对顶角的是( )
D
O
2
1
3
4
E
B
A
C
D
(2)如图所示,直AB、CD相交于O点,OE是射线,则∠1的对顶角是_______,∠4的对顶角是_______ .
∠AOD
∠3
做一做
如图所示,有一个破损的扇形零件,利用图中的量角器可以量出这个扇形零件的圆心角的度数吗?你能说出所量角的度数是多少吗?为什么?
1.画出两个角,使它们的和为90°.
2.画出两个角,使它们的和为180°.
3.用自己的语言描述补角余角的定义.
如果两个角的和是90°,那么称这两个角互为余角. 简称这两个角互余.
如果两个角的和是180°,那么称这两个角互为补角. 简称这两个角互补.
小组交流,互相点评
下列说法正确的有 ____________(填序号)
①已知∠A=40°,则∠A的余角等于50°.
②若∠1+∠2=180°,则∠1和∠2互为补角.
③若∠1+∠2+∠3=180°,则∠1、∠2、∠3互补.
④若∠A=40°26′,则∠A的补角=139°34′.
⑤一个角的补角必为钝角.
⑥一个锐角的补角比这个角的余角大90°.
判断
①②④⑥
做一做
如图,打台球时,选择适当的方向用白球击打红球,反弹后的红球会直接入袋,此时,∠1=∠2.
将左图简化为右图,ON与DC相交所成的∠DON等于90°,且∠1=∠2.
在右图中:
(1)有哪些角互为补角?有哪些角互为余角?
(2)∠3与∠4有什么关系?为什么?
(3)∠AOC与∠BOD有什么关系?为什么?
同角或等角的补角相等,同角或等角的余角相等
随堂练习
1.①.因为∠1+∠2=90?,∠2+∠3=90?,所以∠1=____,理由是______________________.
② 因为∠1+∠2=180?,∠2+∠3=180?,所以∠1=____,理由是______________________.
∠3
同角的余角相等
∠3
同角的补角相等
2.如图,点O在直线AB上,∠DOC和∠BOE都等于90°.
A
O
B
D
C
E
请找出图中互余的角、互补的角、相等的角,并说明理由.先独立探究,再小组交流.
3.如图,直线AB、CD相交于点O,OE平分∠AOB,OB平分∠DOF,若∠DOE=50°,求∠DOF的度数.
解:因为AB为直线,OE平分∠AOB,
所以∠AOE=∠BOE=90°,
因为∠DOE=50°,
所以∠DOB=40°.
因为OB平分∠DOF,
所以∠DOB=∠FOB=40°
所以∠DOF=80°.
4.如图,直线AB、CD相交于点O,OE把∠BOD分成两部分.
(1)图中∠AOC的对顶角是________,∠EOB的邻补角是________.
(2)若∠AOC=70°,且∠BOE∶
∠EOD=2∶3,求∠AOE的度数.
∠BOD
∠AOE
解:因为∠AOC=70°,
所以∠BOD=∠AOC=70°,
因为∠BOE∶∠EOD=2∶3,
所以∠BOE=28°,
所以∠AOE=180°-28°=152°.
课堂小结
谈谈你在这节课中,有什么收获?
课后作业
1.完成课本P40 习题2.1;
2.完成练习册本课时的习题.
1 两条直线的位置关系
情境导入
生活中处处可见道路、房屋、山川、桥梁。在大自然的杰作和人类的创造物中,蕴含着无数的相交线和平行线。我们知道:
在同一平面内,两条直线的位置关系有相交和平行两种.
在同一平面内,不相交的两条直线叫平行线.
探索新知
请动手画出两条直线直线AB和直线CD,交于点O.
观察你所画图形,∠1与∠2的位置有什么关系?它们的大小有什么关系?为什么?与同伴进行交流.
对顶角特征:
1.有公共顶点
2.两边互为反向延长线.
尝试用自己的语言描述对顶角的定义.
归纳总结
直线AB与CD相交于点O,∠1与∠2有公共顶点O,它们的两边互为反向延长线,具有这种位置关系的两个角叫做对顶角.
请你观察图中∠1和∠2这组对顶角,你发现它们的大小有什么关系?
因为∠1+∠3=180°(平角定义)
∠2+∠3=180°(平角定义)
所以∠1=∠2(等量代换)
对顶角相等
对顶角有如下性质:
认一认
(1)下列各图中,∠1与∠2是对顶角的是( )
D
O
2
1
3
4
E
B
A
C
D
(2)如图所示,直AB、CD相交于O点,OE是射线,则∠1的对顶角是_______,∠4的对顶角是_______ .
∠AOD
∠3
做一做
如图所示,有一个破损的扇形零件,利用图中的量角器可以量出这个扇形零件的圆心角的度数吗?你能说出所量角的度数是多少吗?为什么?
1.画出两个角,使它们的和为90°.
2.画出两个角,使它们的和为180°.
3.用自己的语言描述补角余角的定义.
如果两个角的和是90°,那么称这两个角互为余角. 简称这两个角互余.
如果两个角的和是180°,那么称这两个角互为补角. 简称这两个角互补.
小组交流,互相点评
下列说法正确的有 ____________(填序号)
①已知∠A=40°,则∠A的余角等于50°.
②若∠1+∠2=180°,则∠1和∠2互为补角.
③若∠1+∠2+∠3=180°,则∠1、∠2、∠3互补.
④若∠A=40°26′,则∠A的补角=139°34′.
⑤一个角的补角必为钝角.
⑥一个锐角的补角比这个角的余角大90°.
判断
①②④⑥
做一做
如图,打台球时,选择适当的方向用白球击打红球,反弹后的红球会直接入袋,此时,∠1=∠2.
将左图简化为右图,ON与DC相交所成的∠DON等于90°,且∠1=∠2.
在右图中:
(1)有哪些角互为补角?有哪些角互为余角?
(2)∠3与∠4有什么关系?为什么?
(3)∠AOC与∠BOD有什么关系?为什么?
同角或等角的补角相等,同角或等角的余角相等
随堂练习
1.①.因为∠1+∠2=90?,∠2+∠3=90?,所以∠1=____,理由是______________________.
② 因为∠1+∠2=180?,∠2+∠3=180?,所以∠1=____,理由是______________________.
∠3
同角的余角相等
∠3
同角的补角相等
2.如图,点O在直线AB上,∠DOC和∠BOE都等于90°.
A
O
B
D
C
E
请找出图中互余的角、互补的角、相等的角,并说明理由.先独立探究,再小组交流.
3.如图,直线AB、CD相交于点O,OE平分∠AOB,OB平分∠DOF,若∠DOE=50°,求∠DOF的度数.
解:因为AB为直线,OE平分∠AOB,
所以∠AOE=∠BOE=90°,
因为∠DOE=50°,
所以∠DOB=40°.
因为OB平分∠DOF,
所以∠DOB=∠FOB=40°
所以∠DOF=80°.
4.如图,直线AB、CD相交于点O,OE把∠BOD分成两部分.
(1)图中∠AOC的对顶角是________,∠EOB的邻补角是________.
(2)若∠AOC=70°,且∠BOE∶
∠EOD=2∶3,求∠AOE的度数.
∠BOD
∠AOE
解:因为∠AOC=70°,
所以∠BOD=∠AOC=70°,
因为∠BOE∶∠EOD=2∶3,
所以∠BOE=28°,
所以∠AOE=180°-28°=152°.
课堂小结
谈谈你在这节课中,有什么收获?
课后作业
1.完成课本P40 习题2.1;
2.完成练习册本课时的习题.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
