北师大版数学七年级下册课件:4.1.2三角形的三边关系(18张PPT)
文档属性
| 名称 | 北师大版数学七年级下册课件:4.1.2三角形的三边关系(18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 486.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-17 12:39:27 | ||
图片预览



文档简介
北师大版七年级数学下册
第2课时 三角形的三边关系
新课导入
将三角形按角的大小可以分为几类?
锐角三角形 :三个内角都是锐角.
直角三角形 :有一个内角为直角.
钝角三角形 :有一个内角为钝角.
如果按边来分又可以分为几类
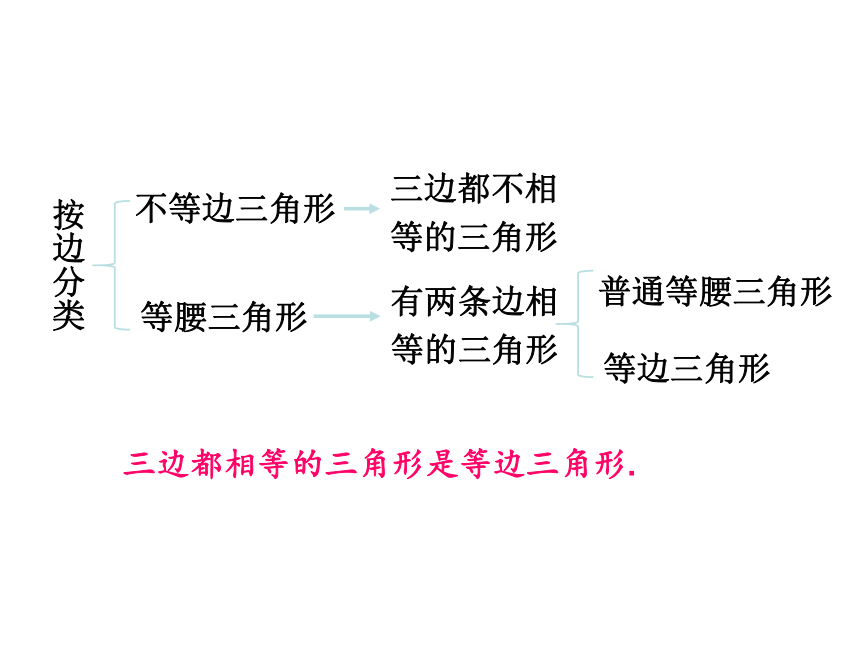
按边分类
不等边三角形
等腰三角形
三边都不相等的三角形
有两条边相等的三角形
普通等腰三角形
等边三角形
三边都相等的三角形是等边三角形.
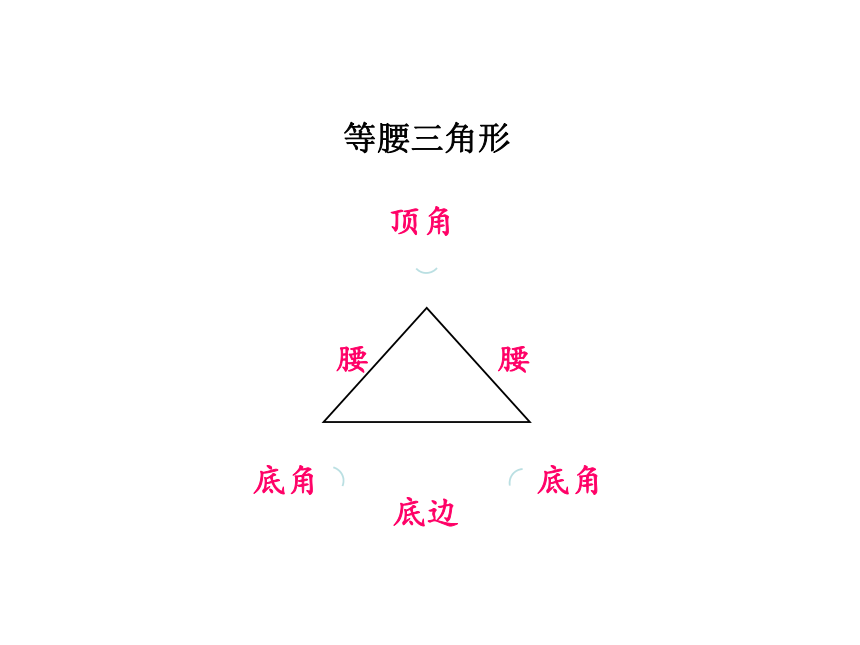
等腰三角形
顶角
底角
底角
底边
腰
腰
议一议
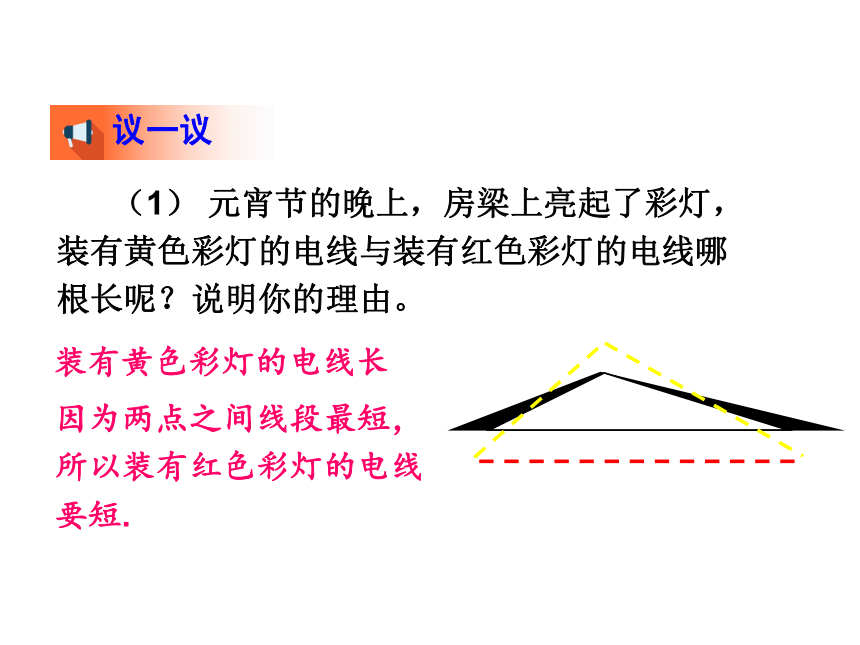
(1) 元宵节的晚上,房梁上亮起了彩灯,装有黄色彩灯的电线与装有红色彩灯的电线哪根长呢?说明你的理由。
装有黄色彩灯的电线长
因为两点之间线段最短,所以装有红色彩灯的电线要短.
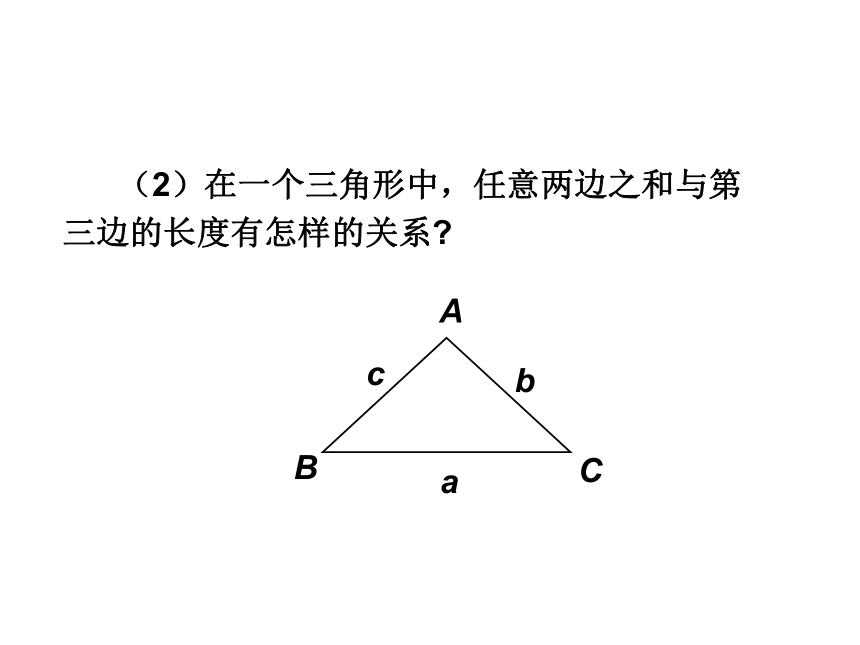
(2)在一个三角形中,任意两边之和与第三边的长度有怎样的关系?
A
B
C
a
b
c
三角形任意两边之和大于第三边
A
B
C
a
b
c
a + b > c
a + c > b
c + b > a
三角形任意两边之差小于第三边
A
B
C
a
b
c
|a – b| < c
|a – c| < b
|c – b| < a
例 有两根长度分别为 5cm 和 8cm 的木棒,用长度为 2cm 的木棒与它们能摆成三角形吗?为什么?长度为 13cm 的木棒呢?
解:取长度为2cm的木棒时,由于2+5=7 < 8,出现了两边之和小于第三边的情况,所以它们不能摆成三角形.
取长度为13cm的木棒时,由于5+8=13,出现了两边之和等于第三边的情况,所以它们也不能摆成三角形.
如果一根木棒能与长度分别为 5 cm 和 8 cm 的两根木棒摆成三角形,那么它的长度取值范围是什么?
想一想
8-5 < x < 5+8
3 < x < 13
随堂演练
1.三条线段的长度分别为:
B
(1)3cm,4cm,5cm;
(2)8cm,7cm,15cm;
(3)13cm,12cm,20cm;(4)5cm,5cm,11cm.
能组成三角形的有( )组.
A.1 B.2 C.3 D.4
2.现有长度分别为1cm,2cm,3cm,4cm,5cm 的五条线段,从其中选三条线段为边可以构成_____个的不同的三角形.
3
3.如果三角形的两边长分别是 2 和 4,且第三边是奇数,那么第三边长为______. 若第三边为偶数,那么三角形的周长______.
3或5
10
4.已知等腰三角形的两边长分别为4、9,求它的周长.
解:因为三角形是等腰三角形,
所以,当腰长为4时,
三角形的三边分别为:4、4、9,而4+4<9,
所以不能构成一个三角形,应舍去.
当腰长为9时,
三角形的三边分别为:9、9、4,4+9>9,
所以能构成一个三角形.
即周长为22.
5.某地有四个汽车停车场,位于如图所示的四边形ABCD 的四个顶点,现在要建立一个汽车维修站,你能利用“三角形任意两边之和大于第三边”在四边形ABCD的内部找一点P,使点 P 到 A,B,C,D 四点的距离之和最小吗?
A
B
C
D
A
B
C
D
H
解:如图所示,连接AC,BD,它们的交点 H 就是汽车维修站的位置.
A
B
C
D
H
H′
理由:任取异于点 H 的点H′,连接AH′、BH′、CH′、DH′,根据三角形的两边之和大于第三边有:
AH′ + H′C > AH + HC,
BH′ + H′D > BH + HD
即 AH + HC + BH + HD 最小.
课堂小结
三角形任意两边之和大于第三边.
三角形任意两边之差小于第三边.
第2课时 三角形的三边关系
新课导入
将三角形按角的大小可以分为几类?
锐角三角形 :三个内角都是锐角.
直角三角形 :有一个内角为直角.
钝角三角形 :有一个内角为钝角.
如果按边来分又可以分为几类
按边分类
不等边三角形
等腰三角形
三边都不相等的三角形
有两条边相等的三角形
普通等腰三角形
等边三角形
三边都相等的三角形是等边三角形.
等腰三角形
顶角
底角
底角
底边
腰
腰
议一议
(1) 元宵节的晚上,房梁上亮起了彩灯,装有黄色彩灯的电线与装有红色彩灯的电线哪根长呢?说明你的理由。
装有黄色彩灯的电线长
因为两点之间线段最短,所以装有红色彩灯的电线要短.
(2)在一个三角形中,任意两边之和与第三边的长度有怎样的关系?
A
B
C
a
b
c
三角形任意两边之和大于第三边
A
B
C
a
b
c
a + b > c
a + c > b
c + b > a
三角形任意两边之差小于第三边
A
B
C
a
b
c
|a – b| < c
|a – c| < b
|c – b| < a
例 有两根长度分别为 5cm 和 8cm 的木棒,用长度为 2cm 的木棒与它们能摆成三角形吗?为什么?长度为 13cm 的木棒呢?
解:取长度为2cm的木棒时,由于2+5=7 < 8,出现了两边之和小于第三边的情况,所以它们不能摆成三角形.
取长度为13cm的木棒时,由于5+8=13,出现了两边之和等于第三边的情况,所以它们也不能摆成三角形.
如果一根木棒能与长度分别为 5 cm 和 8 cm 的两根木棒摆成三角形,那么它的长度取值范围是什么?
想一想
8-5 < x < 5+8
3 < x < 13
随堂演练
1.三条线段的长度分别为:
B
(1)3cm,4cm,5cm;
(2)8cm,7cm,15cm;
(3)13cm,12cm,20cm;(4)5cm,5cm,11cm.
能组成三角形的有( )组.
A.1 B.2 C.3 D.4
2.现有长度分别为1cm,2cm,3cm,4cm,5cm 的五条线段,从其中选三条线段为边可以构成_____个的不同的三角形.
3
3.如果三角形的两边长分别是 2 和 4,且第三边是奇数,那么第三边长为______. 若第三边为偶数,那么三角形的周长______.
3或5
10
4.已知等腰三角形的两边长分别为4、9,求它的周长.
解:因为三角形是等腰三角形,
所以,当腰长为4时,
三角形的三边分别为:4、4、9,而4+4<9,
所以不能构成一个三角形,应舍去.
当腰长为9时,
三角形的三边分别为:9、9、4,4+9>9,
所以能构成一个三角形.
即周长为22.
5.某地有四个汽车停车场,位于如图所示的四边形ABCD 的四个顶点,现在要建立一个汽车维修站,你能利用“三角形任意两边之和大于第三边”在四边形ABCD的内部找一点P,使点 P 到 A,B,C,D 四点的距离之和最小吗?
A
B
C
D
A
B
C
D
H
解:如图所示,连接AC,BD,它们的交点 H 就是汽车维修站的位置.
A
B
C
D
H
H′
理由:任取异于点 H 的点H′,连接AH′、BH′、CH′、DH′,根据三角形的两边之和大于第三边有:
AH′ + H′C > AH + HC,
BH′ + H′D > BH + HD
即 AH + HC + BH + HD 最小.
课堂小结
三角形任意两边之和大于第三边.
三角形任意两边之差小于第三边.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
