第20章 一次函数 单元测试卷 (解析版)
文档属性
| 名称 | 第20章 一次函数 单元测试卷 (解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-17 08:50:02 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第20章
一次函数
单元测试卷
一.选择题(共6小题)
1.下列函数中,一次函数是
A.
B.
C.
D.、是常数)
2.一次函数的图象经过
A.第一、二、三象限
B.第一、三、四象限
C.第一、二、四象限
D.第二、三、四象限
3.点、点在直线上,则
A.
B.
C.
D.无法比较、大小
4.在一次函数中,函数的值随的值增大而减小,那么常数的取值范围是
A.
B.
C.
D.
5.若一次函数的图象不经过第三象限,则、的取值范围是
A.,
B.,
C.,
D.,
6.已知正比例函数与,则它们图象的大致位置不可能的是
A.
B.
C.
D.
二.填空题(共12小题)
7.若函数是一次函数,那么 .
8.已知一次函数,那么 .
9.一次函数的图象不经过第
象限.
10.一次函数与轴的交点坐标是
.
11.已知一次函数的图象经过点,则截距为 .
12.已知函数,当时,自变量的取值范围是 .
13.如果点在一次函数的图象上,那么 .
14.已知一次函数的图象与直线平行,那么 .
15.如果把线沿轴向下平移1个单位,那么得到的直线的表达式为 .
16.已知一次函数,函数值随自变量的值增大而减小,那么的取值范围是 .
17.如图,已知一次函数的图象经过点与,那么关于的不等式的解集是 .
18.小明从家步行到学校需走的路程为1800米.图中的折线反映了小明从家步行到学校所走的路程(米与时间(分钟)的函数关系,根据图象提供的信息,当小明从家出发去学校步行15分钟时,到学校还需步行 米.
三.解答题(共7小题)
19.直线经过点,且截距为8,求直线的解析式.
20.已知点是直线上的一点,若该直线和轴相交于点,求点的坐标.
21.已知函数,
(1)若函数图象经过原点,求的值;
(2)若这个函数是一次函数,且随着的增大而减小,求的取值范围.
22.如图,在平面直角坐标系中,一次函数的图象与正比例函数的图象交于点,与轴交于点.
(1)求、的值;
(2)求的面积.
23.小明从地出发向地行走,同时晓阳从地出发向地行走,小明、晓阳离地的距离(千米)与已用时间(分钟)之间的函数关系分别如图中、所示.
(1)小明与晓阳出发几分钟时相遇?
(2)求晓阳到达地的时间.
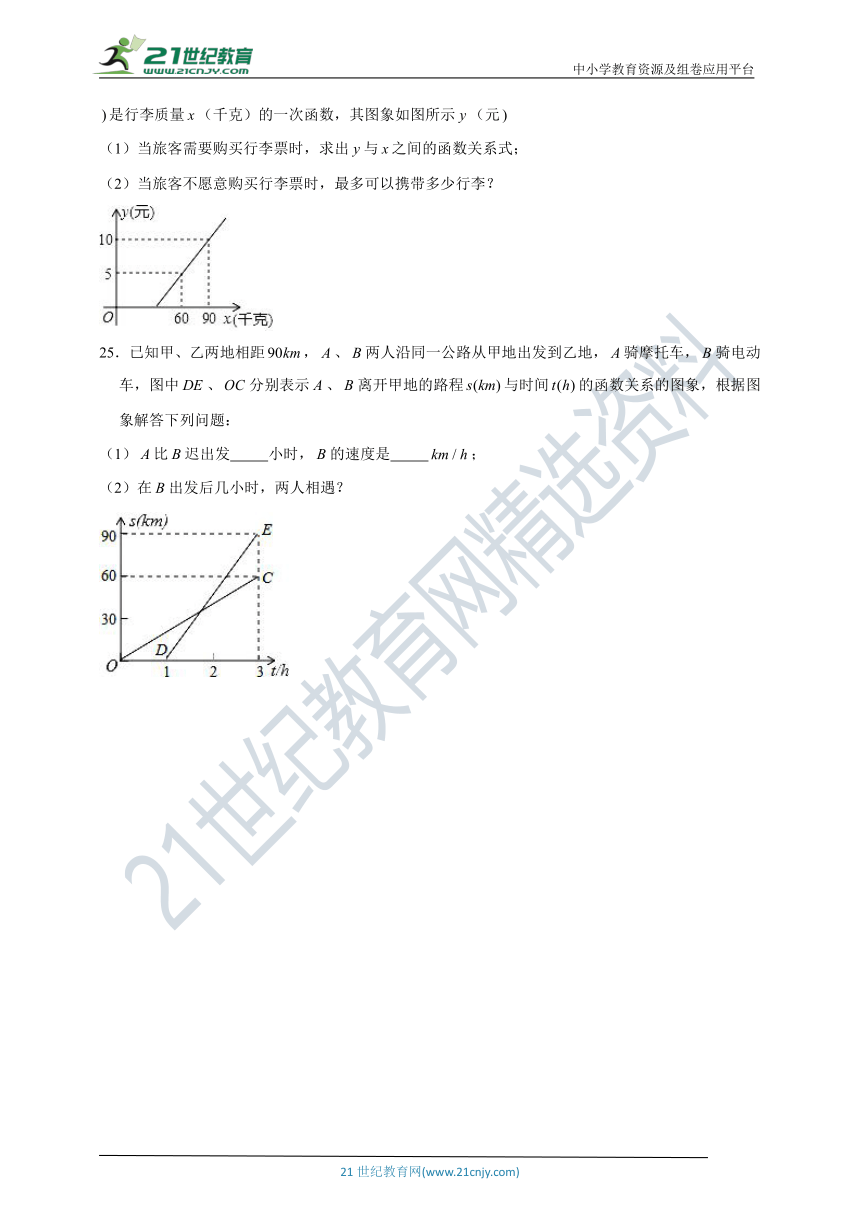
24.旅客乘车按规定可以随身携带一定质量的行李,如果超过规定,则需购买行李票,设行李票(元是行李质量(千克)的一次函数,其图象如图所示(元
(1)当旅客需要购买行李票时,求出与之间的函数关系式;
(2)当旅客不愿意购买行李票时,最多可以携带多少行李?
25.已知甲、乙两地相距,、两人沿同一公路从甲地出发到乙地,骑摩托车,骑电动车,图中、分别表示、离开甲地的路程与时间的函数关系的图象,根据图象解答下列问题:
(1)比迟出发
小时,的速度是
;
(2)在出发后几小时,两人相遇?
参考答案
一.选择题(共6小题)
1.下列函数中,一次函数是
A.
B.
C.
D.、是常数)
解:、自变量在分母上,不符合一次函数定义;
、是二次函数,故选项错误;
、是正比例函数也是一次函数,故选项正确;
、少,不符合一次函数定义;
故选:.
2.一次函数的图象经过
A.第一、二、三象限
B.第一、三、四象限
C.第一、二、四象限
D.第二、三、四象限
解:,
图象经过第一、三象限,
,
图象与轴的交点在轴上方,
一次函数的图象经过第一、二、三象限.
故选:.
3.点、点在直线上,则
A.
B.
C.
D.无法比较、大小
解:点、点在直线上,
,,
,
故选:.
4.在一次函数中,函数的值随的值增大而减小,那么常数的取值范围是
A.
B.
C.
D.
解:由题意得,
解得,
故选:.
5.若一次函数的图象不经过第三象限,则、的取值范围是
A.,
B.,
C.,
D.,
解:一次函数的图象不经过第三象限,
直线经过第一、二、四象限或第二、四象限,
,.
故选:.
6.已知正比例函数与,则它们图象的大致位置不可能的是
A.
B.
C.
D.
解:当时,正比例函数的图象过原点、二、四象限,正比例函数的图象经过原点,一、三象限,符合;
当时,正比例函数的图象过原点、一、三象限,正比例函数的图象经过原点,一、三象限,符合;
当时,正比例函数的图象过原点、一、三象限,正比例函数的图象经过原点,二、四象限,符合;
综上,它们图象的大致位置不可能的是,
故选:.
二.填空题(共12小题)
7.若函数是一次函数,那么 .
解:由题意得,且,
解得:且,
.
故答案为:.
8.已知一次函数,那么 .
解:当时,.
故答案为:.
9.一次函数的图象不经过第 二 象限.
解:一次函数中的,
该函数图象经过第一、三象限.
又,
该函数图象与轴交于负半轴,
该函数图象经过第一、三、四象限,即不经过第二象限.
故答案是:二.
10.一次函数与轴的交点坐标是 .
解:把代入得:,
,
即一次函数与轴的交点坐标是.
故答案为:.
11.已知一次函数的图象经过点,则截距为 3 .
解:一次函数的图象经过点,
,
一次函数的截距为3.
故答案为:3.
12.已知函数,当时,自变量的取值范围是 .
解:,
当时,,解得,
又,
随着的增大而减小,
当时,.
故答案为:.
13.如果点在一次函数的图象上,那么 1 .
解:点在一次函数的图象上,
.
故答案为:1.
14.已知一次函数的图象与直线平行,那么 4 .
解:一次函数的图象与直线平行,
,
,
故答案为:4.
15.如果把线沿轴向下平移1个单位,那么得到的直线的表达式为 .
解:把线沿轴向下平移1个单位,那么得到的直线的表达式为.
故答案为:.
16.已知一次函数,函数值随自变量的值增大而减小,那么的取值范围是 .
解:由题意得,,
解得,;
故答案为.
17.如图,已知一次函数的图象经过点与,那么关于的不等式的解集是 .
解:由题意可得:一次函数中,时,图象在轴下方,,
则关于的不等式的解集是,
故答案为:.
18.小明从家步行到学校需走的路程为1800米.图中的折线反映了小明从家步行到学校所走的路程(米与时间(分钟)的函数关系,根据图象提供的信息,当小明从家出发去学校步行15分钟时,到学校还需步行 350 米.
解:当时,设,
将、代入,得:
,
解得:,
;
当时,,
(米
当小明从家出发去学校步行15分钟时,到学校还需步行350米,
故答案为:350.
三.解答题(共7小题)
19.直线经过点,且截距为8,求直线的解析式.
解:由题意:设直线的解析式为
经过点,
,
解得
所求直线的解析式是.
20.已知点是直线上的一点,若该直线和轴相交于点,求点的坐标.
解:将代入,得:,
解得:,
直线的解析式为.
当时,,
解得:,
点的坐标为,.
21.已知函数,
(1)若函数图象经过原点,求的值;
(2)若这个函数是一次函数,且随着的增大而减小,求的取值范围.
解:(1)把代入,得:,;
(2)根据随的增大而减小说明.即.
解得:.
22.如图,在平面直角坐标系中,一次函数的图象与正比例函数的图象交于点,与轴交于点.
(1)求、的值;
(2)求的面积.
解:(1)正比例函数的图象过点.
.
又一次函数的图象过点.
,
.
(2)一次函数的图象与轴交于点,
,
.
23.小明从地出发向地行走,同时晓阳从地出发向地行走,小明、晓阳离地的距离(千米)与已用时间(分钟)之间的函数关系分别如图中、所示.
(1)小明与晓阳出发几分钟时相遇?
(2)求晓阳到达地的时间.
解:(1)由图象可得,
小明的速度为(千米分钟),
(分钟),
即小明与晓阳出发12分钟时相遇;
(2)晓阳的速度为:(千米分钟),
(分钟),
即晓阳到达地用时20分钟.
24.旅客乘车按规定可以随身携带一定质量的行李,如果超过规定,则需购买行李票,设行李票(元是行李质量(千克)的一次函数,其图象如图所示(元
(1)当旅客需要购买行李票时,求出与之间的函数关系式;
(2)当旅客不愿意购买行李票时,最多可以携带多少行李?
解:(1)设一次函数关系式为,
如图所示,有,
解得,
所以与之间的函数关系式为.
(2)由(1)知,当时,有,
解得.
故旅客最多可免费携带行李30千克.
25.已知甲、乙两地相距,、两人沿同一公路从甲地出发到乙地,骑摩托车,骑电动车,图中、分别表示、离开甲地的路程与时间的函数关系的图象,根据图象解答下列问题:
(1)比迟出发 1 小时,的速度是
;
(2)在出发后几小时,两人相遇?
解:(1)由图象可得,
比迟出发1小时,的速度是:,
故答案为:1,20;
(2)设段对应的函数解析式是,
则,得,
即段对应的函数解析式是,
设段对应的函数解析式是,
,得,
即段对应的函数解析式是,
,得,
出发小时,两人相遇.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
第20章
一次函数
单元测试卷
一.选择题(共6小题)
1.下列函数中,一次函数是
A.
B.
C.
D.、是常数)
2.一次函数的图象经过
A.第一、二、三象限
B.第一、三、四象限
C.第一、二、四象限
D.第二、三、四象限
3.点、点在直线上,则
A.
B.
C.
D.无法比较、大小
4.在一次函数中,函数的值随的值增大而减小,那么常数的取值范围是
A.
B.
C.
D.
5.若一次函数的图象不经过第三象限,则、的取值范围是
A.,
B.,
C.,
D.,
6.已知正比例函数与,则它们图象的大致位置不可能的是
A.
B.
C.
D.
二.填空题(共12小题)
7.若函数是一次函数,那么 .
8.已知一次函数,那么 .
9.一次函数的图象不经过第
象限.
10.一次函数与轴的交点坐标是
.
11.已知一次函数的图象经过点,则截距为 .
12.已知函数,当时,自变量的取值范围是 .
13.如果点在一次函数的图象上,那么 .
14.已知一次函数的图象与直线平行,那么 .
15.如果把线沿轴向下平移1个单位,那么得到的直线的表达式为 .
16.已知一次函数,函数值随自变量的值增大而减小,那么的取值范围是 .
17.如图,已知一次函数的图象经过点与,那么关于的不等式的解集是 .
18.小明从家步行到学校需走的路程为1800米.图中的折线反映了小明从家步行到学校所走的路程(米与时间(分钟)的函数关系,根据图象提供的信息,当小明从家出发去学校步行15分钟时,到学校还需步行 米.
三.解答题(共7小题)
19.直线经过点,且截距为8,求直线的解析式.
20.已知点是直线上的一点,若该直线和轴相交于点,求点的坐标.
21.已知函数,
(1)若函数图象经过原点,求的值;
(2)若这个函数是一次函数,且随着的增大而减小,求的取值范围.
22.如图,在平面直角坐标系中,一次函数的图象与正比例函数的图象交于点,与轴交于点.
(1)求、的值;
(2)求的面积.
23.小明从地出发向地行走,同时晓阳从地出发向地行走,小明、晓阳离地的距离(千米)与已用时间(分钟)之间的函数关系分别如图中、所示.
(1)小明与晓阳出发几分钟时相遇?
(2)求晓阳到达地的时间.
24.旅客乘车按规定可以随身携带一定质量的行李,如果超过规定,则需购买行李票,设行李票(元是行李质量(千克)的一次函数,其图象如图所示(元
(1)当旅客需要购买行李票时,求出与之间的函数关系式;
(2)当旅客不愿意购买行李票时,最多可以携带多少行李?
25.已知甲、乙两地相距,、两人沿同一公路从甲地出发到乙地,骑摩托车,骑电动车,图中、分别表示、离开甲地的路程与时间的函数关系的图象,根据图象解答下列问题:
(1)比迟出发
小时,的速度是
;
(2)在出发后几小时,两人相遇?
参考答案
一.选择题(共6小题)
1.下列函数中,一次函数是
A.
B.
C.
D.、是常数)
解:、自变量在分母上,不符合一次函数定义;
、是二次函数,故选项错误;
、是正比例函数也是一次函数,故选项正确;
、少,不符合一次函数定义;
故选:.
2.一次函数的图象经过
A.第一、二、三象限
B.第一、三、四象限
C.第一、二、四象限
D.第二、三、四象限
解:,
图象经过第一、三象限,
,
图象与轴的交点在轴上方,
一次函数的图象经过第一、二、三象限.
故选:.
3.点、点在直线上,则
A.
B.
C.
D.无法比较、大小
解:点、点在直线上,
,,
,
故选:.
4.在一次函数中,函数的值随的值增大而减小,那么常数的取值范围是
A.
B.
C.
D.
解:由题意得,
解得,
故选:.
5.若一次函数的图象不经过第三象限,则、的取值范围是
A.,
B.,
C.,
D.,
解:一次函数的图象不经过第三象限,
直线经过第一、二、四象限或第二、四象限,
,.
故选:.
6.已知正比例函数与,则它们图象的大致位置不可能的是
A.
B.
C.
D.
解:当时,正比例函数的图象过原点、二、四象限,正比例函数的图象经过原点,一、三象限,符合;
当时,正比例函数的图象过原点、一、三象限,正比例函数的图象经过原点,一、三象限,符合;
当时,正比例函数的图象过原点、一、三象限,正比例函数的图象经过原点,二、四象限,符合;
综上,它们图象的大致位置不可能的是,
故选:.
二.填空题(共12小题)
7.若函数是一次函数,那么 .
解:由题意得,且,
解得:且,
.
故答案为:.
8.已知一次函数,那么 .
解:当时,.
故答案为:.
9.一次函数的图象不经过第 二 象限.
解:一次函数中的,
该函数图象经过第一、三象限.
又,
该函数图象与轴交于负半轴,
该函数图象经过第一、三、四象限,即不经过第二象限.
故答案是:二.
10.一次函数与轴的交点坐标是 .
解:把代入得:,
,
即一次函数与轴的交点坐标是.
故答案为:.
11.已知一次函数的图象经过点,则截距为 3 .
解:一次函数的图象经过点,
,
一次函数的截距为3.
故答案为:3.
12.已知函数,当时,自变量的取值范围是 .
解:,
当时,,解得,
又,
随着的增大而减小,
当时,.
故答案为:.
13.如果点在一次函数的图象上,那么 1 .
解:点在一次函数的图象上,
.
故答案为:1.
14.已知一次函数的图象与直线平行,那么 4 .
解:一次函数的图象与直线平行,
,
,
故答案为:4.
15.如果把线沿轴向下平移1个单位,那么得到的直线的表达式为 .
解:把线沿轴向下平移1个单位,那么得到的直线的表达式为.
故答案为:.
16.已知一次函数,函数值随自变量的值增大而减小,那么的取值范围是 .
解:由题意得,,
解得,;
故答案为.
17.如图,已知一次函数的图象经过点与,那么关于的不等式的解集是 .
解:由题意可得:一次函数中,时,图象在轴下方,,
则关于的不等式的解集是,
故答案为:.
18.小明从家步行到学校需走的路程为1800米.图中的折线反映了小明从家步行到学校所走的路程(米与时间(分钟)的函数关系,根据图象提供的信息,当小明从家出发去学校步行15分钟时,到学校还需步行 350 米.
解:当时,设,
将、代入,得:
,
解得:,
;
当时,,
(米
当小明从家出发去学校步行15分钟时,到学校还需步行350米,
故答案为:350.
三.解答题(共7小题)
19.直线经过点,且截距为8,求直线的解析式.
解:由题意:设直线的解析式为
经过点,
,
解得
所求直线的解析式是.
20.已知点是直线上的一点,若该直线和轴相交于点,求点的坐标.
解:将代入,得:,
解得:,
直线的解析式为.
当时,,
解得:,
点的坐标为,.
21.已知函数,
(1)若函数图象经过原点,求的值;
(2)若这个函数是一次函数,且随着的增大而减小,求的取值范围.
解:(1)把代入,得:,;
(2)根据随的增大而减小说明.即.
解得:.
22.如图,在平面直角坐标系中,一次函数的图象与正比例函数的图象交于点,与轴交于点.
(1)求、的值;
(2)求的面积.
解:(1)正比例函数的图象过点.
.
又一次函数的图象过点.
,
.
(2)一次函数的图象与轴交于点,
,
.
23.小明从地出发向地行走,同时晓阳从地出发向地行走,小明、晓阳离地的距离(千米)与已用时间(分钟)之间的函数关系分别如图中、所示.
(1)小明与晓阳出发几分钟时相遇?
(2)求晓阳到达地的时间.
解:(1)由图象可得,
小明的速度为(千米分钟),
(分钟),
即小明与晓阳出发12分钟时相遇;
(2)晓阳的速度为:(千米分钟),
(分钟),
即晓阳到达地用时20分钟.
24.旅客乘车按规定可以随身携带一定质量的行李,如果超过规定,则需购买行李票,设行李票(元是行李质量(千克)的一次函数,其图象如图所示(元
(1)当旅客需要购买行李票时,求出与之间的函数关系式;
(2)当旅客不愿意购买行李票时,最多可以携带多少行李?
解:(1)设一次函数关系式为,
如图所示,有,
解得,
所以与之间的函数关系式为.
(2)由(1)知,当时,有,
解得.
故旅客最多可免费携带行李30千克.
25.已知甲、乙两地相距,、两人沿同一公路从甲地出发到乙地,骑摩托车,骑电动车,图中、分别表示、离开甲地的路程与时间的函数关系的图象,根据图象解答下列问题:
(1)比迟出发 1 小时,的速度是
;
(2)在出发后几小时,两人相遇?
解:(1)由图象可得,
比迟出发1小时,的速度是:,
故答案为:1,20;
(2)设段对应的函数解析式是,
则,得,
即段对应的函数解析式是,
设段对应的函数解析式是,
,得,
即段对应的函数解析式是,
,得,
出发小时,两人相遇.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
