1锐角函数 第2课时 正弦和余弦 (含答案)
文档属性
| 名称 | 1锐角函数 第2课时 正弦和余弦 (含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 533.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-17 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2020-2021学年九年级数学下册课时作业(北师版)
第一章 直角三角形的边角关系
1 锐角三角形
第2课时 正弦和余弦
一、选择题
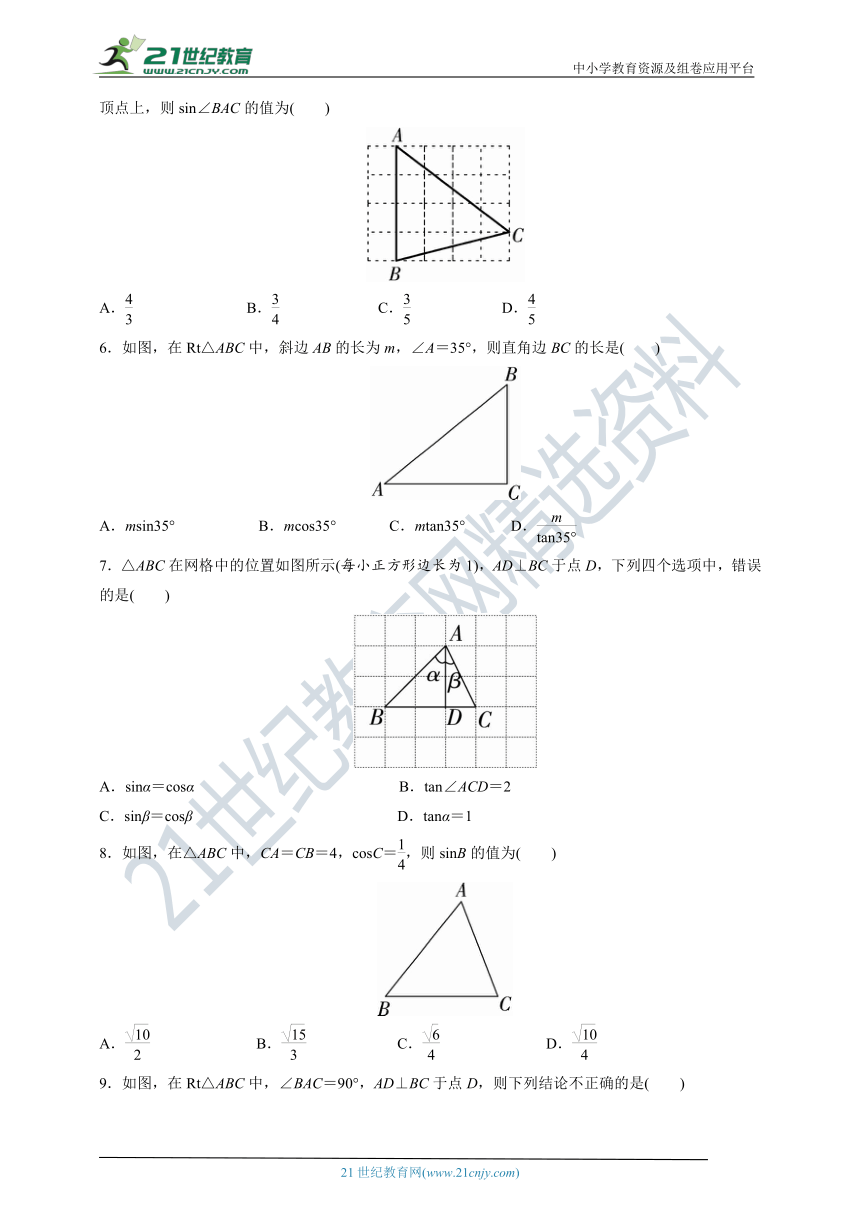
1.如图,在Rt△ABC中,∠C=90°,AC=8,AB=10,则sinB的值是( )
A. B. C. D.
2.如图,P是∠α的边OA上一点,且点P的坐标为(3,4),则sinα的值是( )
A. B. C. D.
3.如图,在平面直角坐标系中,点A的坐标为(4,3),那么cosα的值是( )
A. B. C. D.
4.在△ABC中,若三边BC,CA,AB满足BC∶CA∶AB=5∶12∶13,则cosB的值是( )
A. B. C. D.
5.如图,在5×4的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在这些小正方形的顶点上,则sin∠BAC的值为( )
A. B. C. D.
6.如图,在Rt△ABC中,斜边AB的长为m,∠A=35°,则直角边BC的长是( )
A.msin35° B.mcos35° C.mtan35° D.
7.△ABC在网格中的位置如图所示(每小正方形边长为1),AD⊥BC于点D,下列四个选项中,错误的是( )
A.sinα=cosα B.tan∠ACD=2
C.sinβ=cosβ D.tanα=1
8.如图,在△ABC中,CA=CB=4,cosC=,则sinB的值为( )
A. B. C. D.
9.如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,则下列结论不正确的是( )
A.sinB= B.sinB= C.sinB= D.sinB=
10.在Rt△ABC中,∠C=90°,若AB=4,cosA=,则斜边上的高等于( )
A. B. C. D.
二、填空题
11.如图,一架梯子斜靠在墙上,若梯子底端到墙的距离AC=3米,cos∠BAC=,则梯子长AB=_____米.
12.在直角三角形ABC中,若2AB=AC,则cosC=__________.
13.如图,在△ABC中,DE是BC的垂直平分线,DE交AC于点E,连接BE,若BE=9,BC=12,则cosC=______.
14.如图,在□ABCD中,BC=10,sinB=,AC=BC,则□ABCD的面积是________.
三、解答题
15.在Rt△ABC中,∠B=90°,AB=4,AC=5,求cosA的值.
16.在Rt△ABC中,∠C=90°,∠A,∠B,∠C分别对应边a,b,c,且a=3,c=5,求sinA和cosA的值.
17.如图,已知:在△ABC中,AB=c,BC=a,∠ABC=α,请用α的三角函数及a,c表示△ABC的面积.
18.如图,在△ABC中,∠C=90°,sinA=,AB=15,求△ABC的周长和tanA的值.
19.如图,在△ABC中,AD是BC边上的高,tanB=cos∠DAC.
(1)求证:AC=BD;
(2)若sinC=,BC=12,求AD的长.
参 考 答 案
1. D 2. B 3. D 4. C 5. D 6. A 7. C 8. D 9. C 10. B
11. 4
12. 或
13.
14. 18
15. 解:∵在Rt△ABC中,∠B=90°,AB=4,AC=5,∴cosA==.
16. 解:在Rt△ABC,c=5,a=3,∴b===4,∴sinA==,cosA==.
17. 解:过A作AD⊥BC于点D,则AD=AB·sinB=c·sinα,∴S△ABC=BC·AD=acsinα.
18. 解:在Rt△ABC中,∠C=90°,AB=15,sinA==,∴BC=12,AC===9,∴△ABC的周长为36,tanA==.
19. 解:(1)证明:在Rt△ABD中,tanB=,在Rt△ADC中,cos∠DAC=,又∵tanB=cos∠DAC,∴=,∴AC=BD. (2)在Rt△ADC中,sinC==.设AD=12x,则AC=BD=13x,于是CD=5x.由BD+CD=BC=12,得13x+5x=12,x=,∴AD=12×=8.
_21?????????è?????(www.21cnjy.com)_
2020-2021学年九年级数学下册课时作业(北师版)
第一章 直角三角形的边角关系
1 锐角三角形
第2课时 正弦和余弦
一、选择题
1.如图,在Rt△ABC中,∠C=90°,AC=8,AB=10,则sinB的值是( )
A. B. C. D.
2.如图,P是∠α的边OA上一点,且点P的坐标为(3,4),则sinα的值是( )
A. B. C. D.
3.如图,在平面直角坐标系中,点A的坐标为(4,3),那么cosα的值是( )
A. B. C. D.
4.在△ABC中,若三边BC,CA,AB满足BC∶CA∶AB=5∶12∶13,则cosB的值是( )
A. B. C. D.
5.如图,在5×4的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在这些小正方形的顶点上,则sin∠BAC的值为( )
A. B. C. D.
6.如图,在Rt△ABC中,斜边AB的长为m,∠A=35°,则直角边BC的长是( )
A.msin35° B.mcos35° C.mtan35° D.
7.△ABC在网格中的位置如图所示(每小正方形边长为1),AD⊥BC于点D,下列四个选项中,错误的是( )
A.sinα=cosα B.tan∠ACD=2
C.sinβ=cosβ D.tanα=1
8.如图,在△ABC中,CA=CB=4,cosC=,则sinB的值为( )
A. B. C. D.
9.如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,则下列结论不正确的是( )
A.sinB= B.sinB= C.sinB= D.sinB=
10.在Rt△ABC中,∠C=90°,若AB=4,cosA=,则斜边上的高等于( )
A. B. C. D.
二、填空题
11.如图,一架梯子斜靠在墙上,若梯子底端到墙的距离AC=3米,cos∠BAC=,则梯子长AB=_____米.
12.在直角三角形ABC中,若2AB=AC,则cosC=__________.
13.如图,在△ABC中,DE是BC的垂直平分线,DE交AC于点E,连接BE,若BE=9,BC=12,则cosC=______.
14.如图,在□ABCD中,BC=10,sinB=,AC=BC,则□ABCD的面积是________.
三、解答题
15.在Rt△ABC中,∠B=90°,AB=4,AC=5,求cosA的值.
16.在Rt△ABC中,∠C=90°,∠A,∠B,∠C分别对应边a,b,c,且a=3,c=5,求sinA和cosA的值.
17.如图,已知:在△ABC中,AB=c,BC=a,∠ABC=α,请用α的三角函数及a,c表示△ABC的面积.
18.如图,在△ABC中,∠C=90°,sinA=,AB=15,求△ABC的周长和tanA的值.
19.如图,在△ABC中,AD是BC边上的高,tanB=cos∠DAC.
(1)求证:AC=BD;
(2)若sinC=,BC=12,求AD的长.
参 考 答 案
1. D 2. B 3. D 4. C 5. D 6. A 7. C 8. D 9. C 10. B
11. 4
12. 或
13.
14. 18
15. 解:∵在Rt△ABC中,∠B=90°,AB=4,AC=5,∴cosA==.
16. 解:在Rt△ABC,c=5,a=3,∴b===4,∴sinA==,cosA==.
17. 解:过A作AD⊥BC于点D,则AD=AB·sinB=c·sinα,∴S△ABC=BC·AD=acsinα.
18. 解:在Rt△ABC中,∠C=90°,AB=15,sinA==,∴BC=12,AC===9,∴△ABC的周长为36,tanA==.
19. 解:(1)证明:在Rt△ABD中,tanB=,在Rt△ADC中,cos∠DAC=,又∵tanB=cos∠DAC,∴=,∴AC=BD. (2)在Rt△ADC中,sinC==.设AD=12x,则AC=BD=13x,于是CD=5x.由BD+CD=BC=12,得13x+5x=12,x=,∴AD=12×=8.
_21?????????è?????(www.21cnjy.com)_
