人教版 数学九年级上册 23.2 中心对称 期末复习检测题(Word版 含答案)
文档属性
| 名称 | 人教版 数学九年级上册 23.2 中心对称 期末复习检测题(Word版 含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 606.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-17 00:00:00 | ||
图片预览





文档简介
23.2 中心对称
一、选择题(本大题共8道小题)
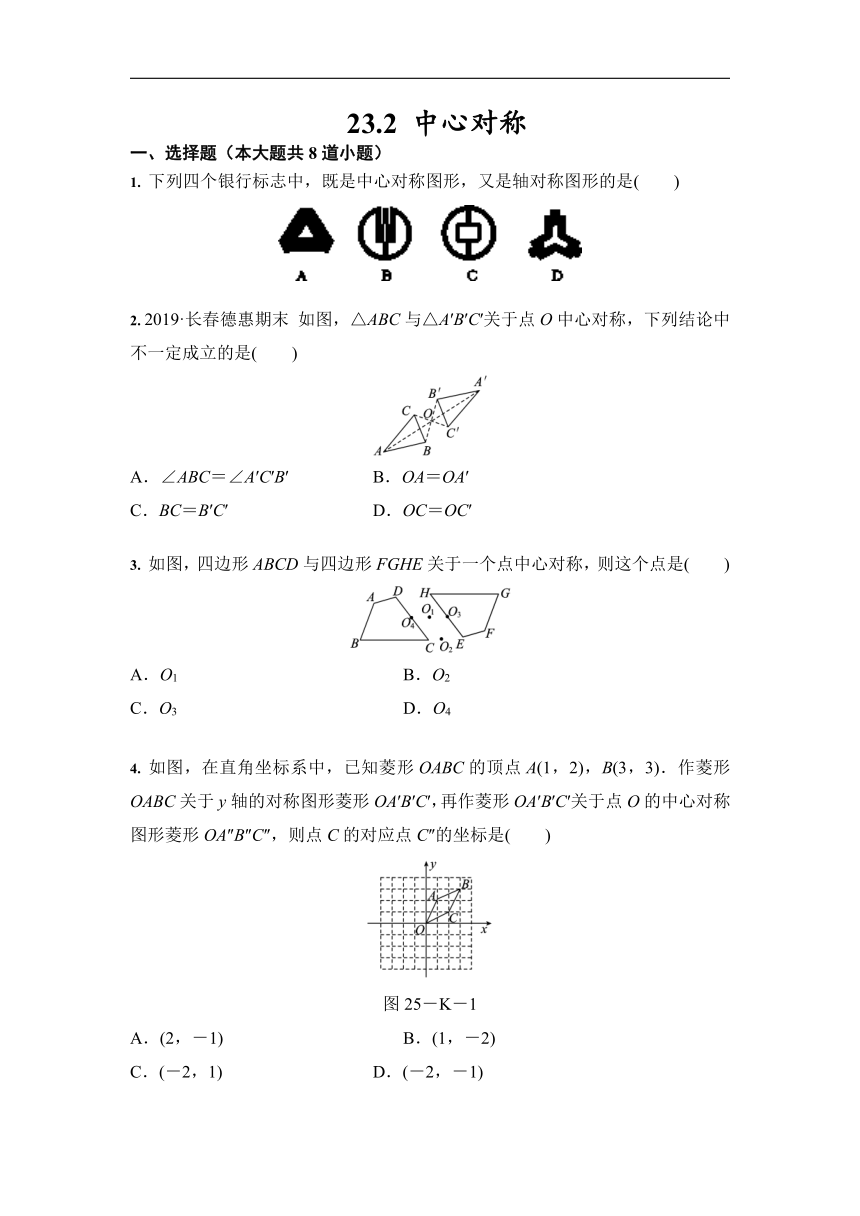
1. 下列四个银行标志中,既是中心对称图形,又是轴对称图形的是( )
2. 2019·长春德惠期末 如图,△ABC与△A′B′C′关于点O中心对称,下列结论中不一定成立的是( )
A.∠ABC=∠A′C′B′ B.OA=OA′
C.BC=B′C′ D.OC=OC′
3. 如图,四边形ABCD与四边形FGHE关于一个点中心对称,则这个点是( )
A.O1 B.O2
C.O3 D.O4
4. 如图,在直角坐标系中,已知菱形OABC的顶点A(1,2),B(3,3).作菱形OABC关于y轴的对称图形菱形OA′B′C′,再作菱形OA′B′C′关于点O的中心对称图形菱形OA″B″C″,则点C的对应点C″的坐标是( )
图25-K-1
A.(2,-1) B.(1,-2)
C.(-2,1) D.(-2,-1)
5. 如图,将△ABC以点O为旋转中心旋转180°后得到△A′B′C′.ED是△ABC的中位线,经旋转后变为线段E′D′.已知BC=4,则线段E′D′的长度为( )
A.2 B.3 C.4 D.1.5
6. 如图示,在Rt△ABC中,∠ACB=90°.P是半圆AC的中点,连接BP交AC于点D.若半圆所在圆的圆心为O,点D,E关于圆心O对称,则图两个阴影部分的面积S1,S2之间的关系是( )
A.S1<S2 B.S1>S2 C.S1=S2 D.不确定
7. 在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1对称,再作△B2A3B3与△B2A2B1关于点B2对称……如此作下去,则△B2nA2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是( )
A.(4n-1,) B.(2n-1,)
C.(4n+1,) D.(2n+1,)
8. 2020·河北模拟 如图所示,A1(1,),A2(,),A3(2,),A4(3,0).作折线OA1A2A3A4关于点A4中心对称的图形,得折线A8A7A6A5A4,再作折线A8A7A6A5A4关于点A8中心对称的图形……以此类推,得到一个大的折线.现有一动点P从原点O出发,沿着折线以每秒1个单位长度的速度运动,设运动时间为t秒.当t=2020时,点P的坐标为( )
A.(1010,) B.(2020,)
C.(2016,0) D.(1010,)
二、填空题(本大题共8道小题)
9. 如图所示,在△ABC中,已知∠ACB=90°,AC=BC=2.若以AC的中点O为旋转中心,将这个三角形旋转180°,点B落在点B′处,则BB′=________.
10. 如图,直线a,b垂直相交于点O,曲线C是以点O为对称中心的中心对称图形,点A的对称点是点A′,AB⊥a于点B,A′D⊥b于点D.若OB=3,OD=2,则阴影部分的面积为________.
11. 如图,将等边三角形AOB放在平面直角坐标系中,点A的坐标为(0,4),点B在第一象限,将△AOB绕点O顺时针旋转180°得到△A′OB′,则点B′的坐标是________.
12. 在平面直角坐标系中,若点A(x+1,2y+1)与点A′(y-2,x)关于原点O对称,则代数式x2-y2的值为________.
13. 如图,将△ABC绕点C(0,1)旋转180°得到△A′B′C,设点A的坐标为(a,b),则点A′的坐标为____________.
14. 2019·呼和浩特 已知正方形的对称中心在坐标原点,顶点A,B,C,D按逆时针依次排列,若点A的坐标为(2,),则点B与点D的坐标分别为( )
A.(-2,),(2,-)
B.(-,2),(,-2)
C.(-,2),(2,-)
D.(-,),(,-)
15. 如图,在平面直角坐标系中,对点P(1,0)作如下变换:先向上平移(后一次平移比前一次多1个单位长度),再作关于原点的对称点,即向上平移1个单位长度得到点P1,作点P1关于原点的对称点P2,向上平移2个单位长度得到点P3,作点P3关于原点的对称点P4……那么点P2020的坐标为____________.
16. 如果将点P绕定点M旋转180°后与点Q重合,那么点P与点Q关于点M对称,定点M叫做对称中心,此时,M是线段PQ的中点.如图3,在平面直角坐标系中,△ABO的顶点A,B,O的坐标分别为(1,0),(0,1),(0,0),点P1,P2,P3,…中的相邻两点都关于△ABO的一个顶点对称,点P1与点P2关于点A对称,点P2与点P3关于点B对称,点P3与点P4关于点O对称,点P4与点P5关于点A对称,点P5与点P6关于点B对称,点P6与点P7关于点O对称……且这些对称中心依次循环.已知点P1的坐标是(1,1),则点P2020的坐标为________.
三、解答题(本大题共4道小题)
17. 如图,△ABO与△CDO关于点O中心对称,点E,F在线段AC上,且AF=CE.求证:DF=BE.
18. 如图,在正方形网格中,△ABC的三个顶点都在格点上,点A,B,C的坐标分别为(-2,4),(-2,0),(-4,1),结合所给的平面直角坐标系解答下列问题:
(1)画出△ABC关于原点O对称的△A1B1C1;
(2)平移△ABC,使点A移动到点A2(0,2)的位置,画出平移后的△A2B2C2,并写出点B2,C2的坐标;
(3)在△ABC,△A1B1C1中,△A2B2C2与________成中心对称,其对称中心的坐标为________.
19. [材料阅读]在平面直角坐标系中,以任意两点P(x1,y1),Q(x2,y2)为端点的线段的中点坐标为.
[运用](1)已知点A(-2,1)和点B(4,-3),则线段AB的中点坐标是________;已知点M(2,3),线段MN的中点坐标是(-2,-1),则点N的坐标是________.
(2)已知平面上四点A(0,0),B(10,0),C(10,6),D(0,6).直线y=mx-3m+2将四边形ABCD分成面积相等的两部分,则m的值为________.
(3)在平面直角坐标系中,有A(-1,2),B(3,1),C(1,4)三点,另有一点D,可使以点A,B,C,D为顶点的四边形为平行四边形,求点D的坐标.
20. 如图,在平面直角坐标系中,△ABC各顶点的坐标分别为A(-2,-2),B(-4,-1),C(-4,-4).
(1)作出△ABC关于原点O成中心对称的△A1B1C1.
(2)作出点A关于x轴的对称点A′.若把点A′向右平移a个单位长度后落在△A1B1C1的内部(不包括顶点和边界),求a的取值范围.
人教版 九年级数学 23.2 中心对称 培优训练-答案
一、选择题(本大题共8道小题)
1. 【答案】C
2. 【答案】A
3. 【答案】A [解析] 如图,连接HC和DE交于点O1.
4. 【答案】A [解析] ∵点C的坐标为(2,1),∴点C′的坐标为(-2,1),∴点C″的坐标为(2,-1).故选A.
5. 【答案】A [解析] ∵ED是△ABC的中位线,BC=4,∴ED=2.又∵△A′B′C′和△ABC关于点O中心对称,∴E′D′=ED=2.
6. 【答案】C [解析] ∵P是半圆AC的中点,∴半圆关于直线OP对称,且点D,E关于圆心O对称,因而S1,S2在直径AC上面的部分面积相等.∵OD=OE,∴CD=AE.∵△CDB的底边CD与△AEB的底边AE相等,高相同,∴它们的面积相等,∴S1=S2.
7. 【答案】C [解析] A1(1,),A2(3,-),A3(5,),A4(7,-),…,
∴点An的坐标为
∵2n+1是奇数,∴点A2n+1的坐标是(4n+1,).故选C.
8. 【答案】A
二、填空题(本大题共8道小题)
9. 【答案】2 [解析] ∵△ABC绕AC的中点O旋转了180°,
∴OB=OB′,∴BB′=2OB.
又∵OC=OA=AC=1,BC=2,
∴在Rt△OBC中,OB===,
∴BB′=2OB=2 .
10. 【答案】6 [解析] 如图,过点A′作A′B′⊥a,垂足为B′,由题意可知,①与②关于点O中心对称,所以阴影部分的面积可以看作四边形A′B′OD的面积.又A′D⊥b于点D,直线a,b互相垂直,可得四边形A′B′OD是矩形,所以其面积为3×2=6.
11. 【答案】(-2 ,-2) [解析] 过点B作BH⊥y轴于点H,如图.∵△OAB为等边三角形,A(0,4),∴OH=AH=2,∠BOA=60°,∴BH=OH=2 ,∴点B的坐标为(2 ,2).∵将△AOB绕点O顺时针旋转180°得到△A′OB′,∴点B′的坐标是(-2 ,-2).
12. 【答案】5 [解析] ∵点A(x+1,2y+1)与点A′(y-2,x)关于原点O对称,
∴解得
故x2-y2=9-4=5.
故答案为5.
13. 【答案】(-a,-b+2) [解析] 如图,过点A作AD⊥y轴于点D,过点A′作A′D′⊥y轴于点D′,则△ACD≌△A′CD′,∴A′D′=AD=a,CD′=CD=-b+1,∴OD′=-b+2,∴点A′的坐标为(-a,-b+2).
14. 【答案】B
15. 【答案】(1,-505)
[解析] 根据题意可列出下面的表格:
观察表格可知:这些点平均分布在四个象限中,序号除以4余1的点在第一象限,横坐标都是1,纵坐标为序号减1除以4的商加1;序号除以4余2的点是序号除以4余1的点关于原点的对称点;序号能被4整除的点在第四象限,横坐标为1,纵坐标为序号除以4的商的相反数;序号除以4余3的点在第二象限,是序号能被4整除的点关于原点的对称点.因为2020÷4=505,所以点P2020在第四象限,坐标为(1,-505).
16. 【答案】(1,-3) [解析] 由题意可得点P2(1,-1),P3(-1,3),P4(1,-3),P5(1,3),P6(-1,-1),P7(1,1),可知6个点一个循环,2020÷6=336……4,故点P2020的坐标与点P4的坐标相同,为(1,-3).
三、解答题(本大题共4道小题)
17. 【答案】
证明:∵△ABO与△CDO关于点O中心对称,
∴BO=DO,AO=CO.
∵AF=CE,∴AO-AF=CO-CE,
即FO=EO.
在△FOD和△EOB中,
∴△FOD≌△EOB(SAS),
∴DF=BE.
18. 【答案】
解:(1)△ABC关于原点O对称的△A1B1C1如图所示.
(2)平移后的△A2B2C2如图所示,其中点B2的坐标为(0,-2),点C2的坐标为(-2,-1).
(3)△A1B1C1 (1,-1)
19. 【答案】
解:(1)(1,-1) (-6,-5)
(2)
(3)设点D的坐标为(x,y).
若以AB为对角线,AC,BC为邻边的四边形为平行四边形,则AB,CD的中点重合,
∴解得
若以BC为对角线,AB,AC为邻边的四边形为平行四边形,则AD,BC的中点重合,
∴
解得
若以AC为对角线,AB,BC为邻边的四边形为平行四边形,则BD,AC的中点重合,
∴
解得
综上可知,点D的坐标为(1,-1)或(5,3)或(-3,5).
20. 【答案】
【思维教练】要作△ABC关于点O的中心对称图形,可先分别求出点A,B,C关于点O 中心对称点,再顺次连接即可;(2)先作出点A′,再根据点A′在ΔA1B1C1,从而得出平移距离a满足A′A1解:(1)如解图,△A1B1C1就是所求作的图形:(2分)
(2)A′如图所示;(4分)
a的取值范围是4<a<6.(6分)
一、选择题(本大题共8道小题)
1. 下列四个银行标志中,既是中心对称图形,又是轴对称图形的是( )
2. 2019·长春德惠期末 如图,△ABC与△A′B′C′关于点O中心对称,下列结论中不一定成立的是( )
A.∠ABC=∠A′C′B′ B.OA=OA′
C.BC=B′C′ D.OC=OC′
3. 如图,四边形ABCD与四边形FGHE关于一个点中心对称,则这个点是( )
A.O1 B.O2
C.O3 D.O4
4. 如图,在直角坐标系中,已知菱形OABC的顶点A(1,2),B(3,3).作菱形OABC关于y轴的对称图形菱形OA′B′C′,再作菱形OA′B′C′关于点O的中心对称图形菱形OA″B″C″,则点C的对应点C″的坐标是( )
图25-K-1
A.(2,-1) B.(1,-2)
C.(-2,1) D.(-2,-1)
5. 如图,将△ABC以点O为旋转中心旋转180°后得到△A′B′C′.ED是△ABC的中位线,经旋转后变为线段E′D′.已知BC=4,则线段E′D′的长度为( )
A.2 B.3 C.4 D.1.5
6. 如图示,在Rt△ABC中,∠ACB=90°.P是半圆AC的中点,连接BP交AC于点D.若半圆所在圆的圆心为O,点D,E关于圆心O对称,则图两个阴影部分的面积S1,S2之间的关系是( )
A.S1<S2 B.S1>S2 C.S1=S2 D.不确定
7. 在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1对称,再作△B2A3B3与△B2A2B1关于点B2对称……如此作下去,则△B2nA2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是( )
A.(4n-1,) B.(2n-1,)
C.(4n+1,) D.(2n+1,)
8. 2020·河北模拟 如图所示,A1(1,),A2(,),A3(2,),A4(3,0).作折线OA1A2A3A4关于点A4中心对称的图形,得折线A8A7A6A5A4,再作折线A8A7A6A5A4关于点A8中心对称的图形……以此类推,得到一个大的折线.现有一动点P从原点O出发,沿着折线以每秒1个单位长度的速度运动,设运动时间为t秒.当t=2020时,点P的坐标为( )
A.(1010,) B.(2020,)
C.(2016,0) D.(1010,)
二、填空题(本大题共8道小题)
9. 如图所示,在△ABC中,已知∠ACB=90°,AC=BC=2.若以AC的中点O为旋转中心,将这个三角形旋转180°,点B落在点B′处,则BB′=________.
10. 如图,直线a,b垂直相交于点O,曲线C是以点O为对称中心的中心对称图形,点A的对称点是点A′,AB⊥a于点B,A′D⊥b于点D.若OB=3,OD=2,则阴影部分的面积为________.
11. 如图,将等边三角形AOB放在平面直角坐标系中,点A的坐标为(0,4),点B在第一象限,将△AOB绕点O顺时针旋转180°得到△A′OB′,则点B′的坐标是________.
12. 在平面直角坐标系中,若点A(x+1,2y+1)与点A′(y-2,x)关于原点O对称,则代数式x2-y2的值为________.
13. 如图,将△ABC绕点C(0,1)旋转180°得到△A′B′C,设点A的坐标为(a,b),则点A′的坐标为____________.
14. 2019·呼和浩特 已知正方形的对称中心在坐标原点,顶点A,B,C,D按逆时针依次排列,若点A的坐标为(2,),则点B与点D的坐标分别为( )
A.(-2,),(2,-)
B.(-,2),(,-2)
C.(-,2),(2,-)
D.(-,),(,-)
15. 如图,在平面直角坐标系中,对点P(1,0)作如下变换:先向上平移(后一次平移比前一次多1个单位长度),再作关于原点的对称点,即向上平移1个单位长度得到点P1,作点P1关于原点的对称点P2,向上平移2个单位长度得到点P3,作点P3关于原点的对称点P4……那么点P2020的坐标为____________.
16. 如果将点P绕定点M旋转180°后与点Q重合,那么点P与点Q关于点M对称,定点M叫做对称中心,此时,M是线段PQ的中点.如图3,在平面直角坐标系中,△ABO的顶点A,B,O的坐标分别为(1,0),(0,1),(0,0),点P1,P2,P3,…中的相邻两点都关于△ABO的一个顶点对称,点P1与点P2关于点A对称,点P2与点P3关于点B对称,点P3与点P4关于点O对称,点P4与点P5关于点A对称,点P5与点P6关于点B对称,点P6与点P7关于点O对称……且这些对称中心依次循环.已知点P1的坐标是(1,1),则点P2020的坐标为________.
三、解答题(本大题共4道小题)
17. 如图,△ABO与△CDO关于点O中心对称,点E,F在线段AC上,且AF=CE.求证:DF=BE.
18. 如图,在正方形网格中,△ABC的三个顶点都在格点上,点A,B,C的坐标分别为(-2,4),(-2,0),(-4,1),结合所给的平面直角坐标系解答下列问题:
(1)画出△ABC关于原点O对称的△A1B1C1;
(2)平移△ABC,使点A移动到点A2(0,2)的位置,画出平移后的△A2B2C2,并写出点B2,C2的坐标;
(3)在△ABC,△A1B1C1中,△A2B2C2与________成中心对称,其对称中心的坐标为________.
19. [材料阅读]在平面直角坐标系中,以任意两点P(x1,y1),Q(x2,y2)为端点的线段的中点坐标为.
[运用](1)已知点A(-2,1)和点B(4,-3),则线段AB的中点坐标是________;已知点M(2,3),线段MN的中点坐标是(-2,-1),则点N的坐标是________.
(2)已知平面上四点A(0,0),B(10,0),C(10,6),D(0,6).直线y=mx-3m+2将四边形ABCD分成面积相等的两部分,则m的值为________.
(3)在平面直角坐标系中,有A(-1,2),B(3,1),C(1,4)三点,另有一点D,可使以点A,B,C,D为顶点的四边形为平行四边形,求点D的坐标.
20. 如图,在平面直角坐标系中,△ABC各顶点的坐标分别为A(-2,-2),B(-4,-1),C(-4,-4).
(1)作出△ABC关于原点O成中心对称的△A1B1C1.
(2)作出点A关于x轴的对称点A′.若把点A′向右平移a个单位长度后落在△A1B1C1的内部(不包括顶点和边界),求a的取值范围.
人教版 九年级数学 23.2 中心对称 培优训练-答案
一、选择题(本大题共8道小题)
1. 【答案】C
2. 【答案】A
3. 【答案】A [解析] 如图,连接HC和DE交于点O1.
4. 【答案】A [解析] ∵点C的坐标为(2,1),∴点C′的坐标为(-2,1),∴点C″的坐标为(2,-1).故选A.
5. 【答案】A [解析] ∵ED是△ABC的中位线,BC=4,∴ED=2.又∵△A′B′C′和△ABC关于点O中心对称,∴E′D′=ED=2.
6. 【答案】C [解析] ∵P是半圆AC的中点,∴半圆关于直线OP对称,且点D,E关于圆心O对称,因而S1,S2在直径AC上面的部分面积相等.∵OD=OE,∴CD=AE.∵△CDB的底边CD与△AEB的底边AE相等,高相同,∴它们的面积相等,∴S1=S2.
7. 【答案】C [解析] A1(1,),A2(3,-),A3(5,),A4(7,-),…,
∴点An的坐标为
∵2n+1是奇数,∴点A2n+1的坐标是(4n+1,).故选C.
8. 【答案】A
二、填空题(本大题共8道小题)
9. 【答案】2 [解析] ∵△ABC绕AC的中点O旋转了180°,
∴OB=OB′,∴BB′=2OB.
又∵OC=OA=AC=1,BC=2,
∴在Rt△OBC中,OB===,
∴BB′=2OB=2 .
10. 【答案】6 [解析] 如图,过点A′作A′B′⊥a,垂足为B′,由题意可知,①与②关于点O中心对称,所以阴影部分的面积可以看作四边形A′B′OD的面积.又A′D⊥b于点D,直线a,b互相垂直,可得四边形A′B′OD是矩形,所以其面积为3×2=6.
11. 【答案】(-2 ,-2) [解析] 过点B作BH⊥y轴于点H,如图.∵△OAB为等边三角形,A(0,4),∴OH=AH=2,∠BOA=60°,∴BH=OH=2 ,∴点B的坐标为(2 ,2).∵将△AOB绕点O顺时针旋转180°得到△A′OB′,∴点B′的坐标是(-2 ,-2).
12. 【答案】5 [解析] ∵点A(x+1,2y+1)与点A′(y-2,x)关于原点O对称,
∴解得
故x2-y2=9-4=5.
故答案为5.
13. 【答案】(-a,-b+2) [解析] 如图,过点A作AD⊥y轴于点D,过点A′作A′D′⊥y轴于点D′,则△ACD≌△A′CD′,∴A′D′=AD=a,CD′=CD=-b+1,∴OD′=-b+2,∴点A′的坐标为(-a,-b+2).
14. 【答案】B
15. 【答案】(1,-505)
[解析] 根据题意可列出下面的表格:
观察表格可知:这些点平均分布在四个象限中,序号除以4余1的点在第一象限,横坐标都是1,纵坐标为序号减1除以4的商加1;序号除以4余2的点是序号除以4余1的点关于原点的对称点;序号能被4整除的点在第四象限,横坐标为1,纵坐标为序号除以4的商的相反数;序号除以4余3的点在第二象限,是序号能被4整除的点关于原点的对称点.因为2020÷4=505,所以点P2020在第四象限,坐标为(1,-505).
16. 【答案】(1,-3) [解析] 由题意可得点P2(1,-1),P3(-1,3),P4(1,-3),P5(1,3),P6(-1,-1),P7(1,1),可知6个点一个循环,2020÷6=336……4,故点P2020的坐标与点P4的坐标相同,为(1,-3).
三、解答题(本大题共4道小题)
17. 【答案】
证明:∵△ABO与△CDO关于点O中心对称,
∴BO=DO,AO=CO.
∵AF=CE,∴AO-AF=CO-CE,
即FO=EO.
在△FOD和△EOB中,
∴△FOD≌△EOB(SAS),
∴DF=BE.
18. 【答案】
解:(1)△ABC关于原点O对称的△A1B1C1如图所示.
(2)平移后的△A2B2C2如图所示,其中点B2的坐标为(0,-2),点C2的坐标为(-2,-1).
(3)△A1B1C1 (1,-1)
19. 【答案】
解:(1)(1,-1) (-6,-5)
(2)
(3)设点D的坐标为(x,y).
若以AB为对角线,AC,BC为邻边的四边形为平行四边形,则AB,CD的中点重合,
∴解得
若以BC为对角线,AB,AC为邻边的四边形为平行四边形,则AD,BC的中点重合,
∴
解得
若以AC为对角线,AB,BC为邻边的四边形为平行四边形,则BD,AC的中点重合,
∴
解得
综上可知,点D的坐标为(1,-1)或(5,3)或(-3,5).
20. 【答案】
【思维教练】要作△ABC关于点O的中心对称图形,可先分别求出点A,B,C关于点O 中心对称点,再顺次连接即可;(2)先作出点A′,再根据点A′在ΔA1B1C1,从而得出平移距离a满足A′A1
(2)A′如图所示;(4分)
a的取值范围是4<a<6.(6分)
同课章节目录
