湘教版七年级数学上册1.2.3绝对值课件(21张)
文档属性
| 名称 | 湘教版七年级数学上册1.2.3绝对值课件(21张) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-17 00:00:00 | ||
图片预览






文档简介
(共21张PPT)
数轴、相反数与绝对值
1.2.3
O
0
-1
-2
-3
-4
-5
1
2
4
5
4
-4的绝对值
3的绝对值
做一做:
1.选择:
-5的相反数是
(
)
A.
5
B.
-5
C.
D.
±5
2.填空:
(1)
0的相反数是
.
(2)
-(+1)=
,-(-0.5)=
.
A
0
-1
0.5
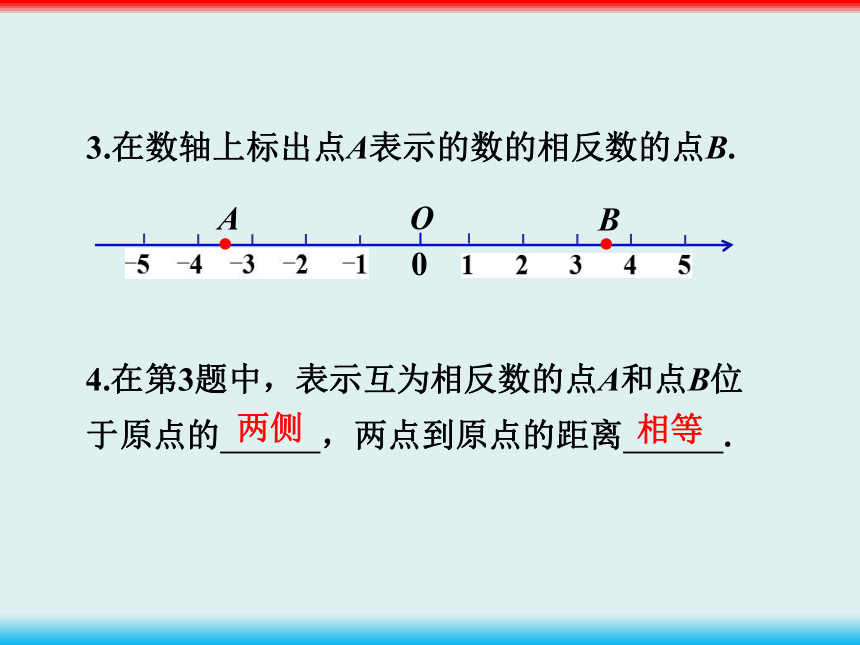
3.在数轴上标出点A表示的数的相反数的点B.
O
0
A
B
4.在第3题中,表示互为相反数的点A和点B位于原点的
,两点到原点的距离
.
两侧
相等
学习目标:
1.理解一个数的绝对值的意义,知道绝对
值的表示方法;
2.能够写出正数、零和负数的绝对值;能
够根据绝对值写数;
3.培养观察能力、抽象概括能力以及用“数
形结合”的数学思想解决问题的能力。
给“一个数与原点的距离”一个新概念——绝对值.这就是
我们这节课要学习的内容.
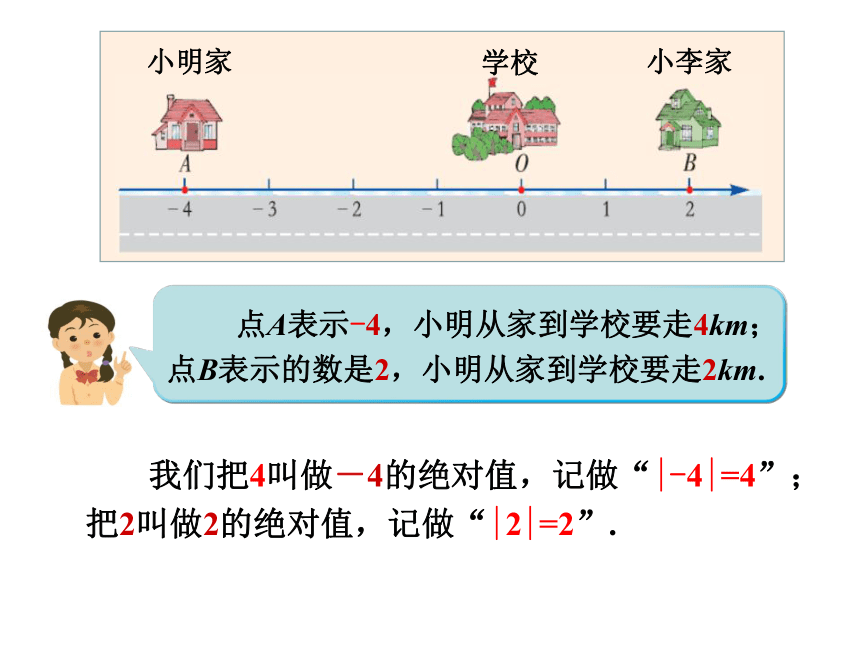
小明家、学校、小李家在数轴上的位置分别如图1-11中点A,B所示.若数轴的单位长度表示1km,则A,B两点表示的有理数分别是多少?小明、小李各自从家到学校要走多远?
小明家
学校
小李家
小明家
学校
小李家
我们把4叫做-4的绝对值,记做“|-4|=4”;
把2叫做2的绝对值,记做“|2|=2”.
问题:
1.正数的绝对值是它本身吗?
2.负数的绝对值是什么数?
3.0的绝对值是0吗?
4.互为相反数的两个数的绝对值相等吗?
一般地,数学上规定:
正数的绝对值是它本身;
负数的绝对值是它的相反数;
0的绝对值是0.
从而互为相反数的两个数的绝对值
.
相等
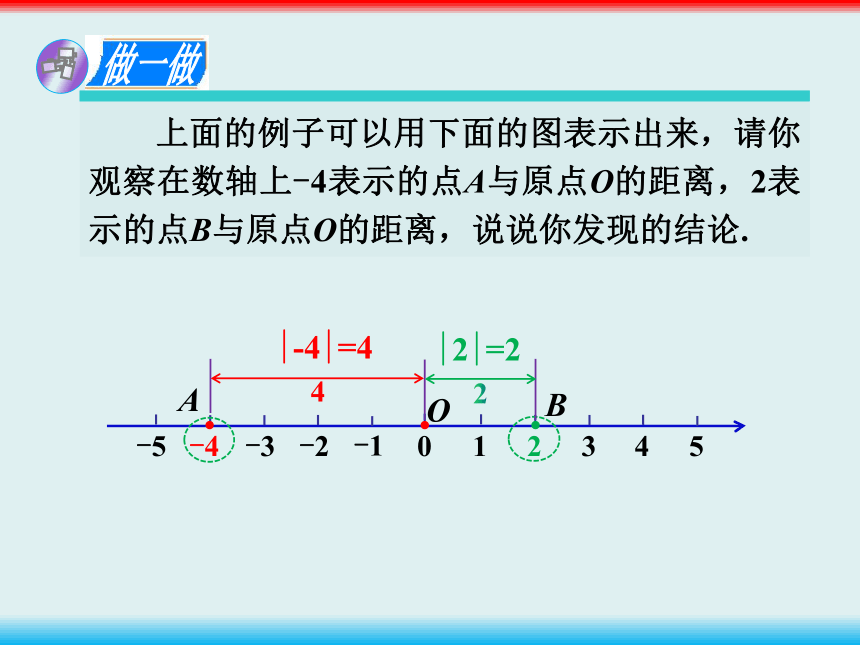
上面的例子可以用下面的图表示出来,请你观察在数轴上-4表示的点A与原点O的距离,2表示的点B与原点O的距离,说说你发现的结论.
O
0
-1
-2
-3
-4
-5
1
2
3
4
5
4
|-4|=4
|2|=2
A
B
O
0
-1
-2
-3
-4
-5
1
2
3
4
5
4
|-4|=4
|2|=2
A
B
一般地,有下述结论:
例5
求下列各数的绝对值:
12,
,-7.5,0.
解
|12|=
;
=
;
|-7.5|=
;
|0|=
.
12
3
5
7.5
0
绝对值一定是一个非负数.
如果a表示一个数,则|a|等于多少?
一般地,如果a表示一个数,则
(1)当a是正数时,|a|=a;
(2)当a=0时,|a|=0;
(3)当a是负数时,|a|=-a.
即|a|是指a和-a中非负数的那一个.
例6
若|a|=8.7,求a.
解
因为绝对值等于8.7的有理数有8.7和-8.7两个,所以a=8.7或a=-8.7.
练习
1.求下列各数的绝对值:
3,3.14,
,-2.8.
3
1
5
3.14
2.8
解
|3|=
;
|3.14|
=
;
=
;
|-2.8|=
.
2.填空:
-|-2018|=
;
-|-2.8|=
;
=
.
2018
-2.8
5
8
3.画一条数轴,并标出表示绝对值等于2,3.5的数的点.
解
绝对值等于2的数有2和-2,在数轴上分别用点A和点B表示;绝对值等于3.5的数有3.5和-3.5,分别用点C和点D表示.如下图:
O
0
-1
-2
-3
-4
-5
1
2
3
4
5
A
B
C
D
交流反思:
这节课你学到了哪些知识?
我学到了:绝对值一定是一个非负数.
我学到了求一个数的绝对值的方法:
|a|=
a
(a为正数时)
0
(a=0时)
-a
(a为负数时)
同学们积极投入学习,收获多多,每人获奖状一张.
作业
习题1.2第6、7、8、12题。
数轴、相反数与绝对值
1.2.3
O
0
-1
-2
-3
-4
-5
1
2
4
5
4
-4的绝对值
3的绝对值
做一做:
1.选择:
-5的相反数是
(
)
A.
5
B.
-5
C.
D.
±5
2.填空:
(1)
0的相反数是
.
(2)
-(+1)=
,-(-0.5)=
.
A
0
-1
0.5
3.在数轴上标出点A表示的数的相反数的点B.
O
0
A
B
4.在第3题中,表示互为相反数的点A和点B位于原点的
,两点到原点的距离
.
两侧
相等
学习目标:
1.理解一个数的绝对值的意义,知道绝对
值的表示方法;
2.能够写出正数、零和负数的绝对值;能
够根据绝对值写数;
3.培养观察能力、抽象概括能力以及用“数
形结合”的数学思想解决问题的能力。
给“一个数与原点的距离”一个新概念——绝对值.这就是
我们这节课要学习的内容.
小明家、学校、小李家在数轴上的位置分别如图1-11中点A,B所示.若数轴的单位长度表示1km,则A,B两点表示的有理数分别是多少?小明、小李各自从家到学校要走多远?
小明家
学校
小李家
小明家
学校
小李家
我们把4叫做-4的绝对值,记做“|-4|=4”;
把2叫做2的绝对值,记做“|2|=2”.
问题:
1.正数的绝对值是它本身吗?
2.负数的绝对值是什么数?
3.0的绝对值是0吗?
4.互为相反数的两个数的绝对值相等吗?
一般地,数学上规定:
正数的绝对值是它本身;
负数的绝对值是它的相反数;
0的绝对值是0.
从而互为相反数的两个数的绝对值
.
相等
上面的例子可以用下面的图表示出来,请你观察在数轴上-4表示的点A与原点O的距离,2表示的点B与原点O的距离,说说你发现的结论.
O
0
-1
-2
-3
-4
-5
1
2
3
4
5
4
|-4|=4
|2|=2
A
B
O
0
-1
-2
-3
-4
-5
1
2
3
4
5
4
|-4|=4
|2|=2
A
B
一般地,有下述结论:
例5
求下列各数的绝对值:
12,
,-7.5,0.
解
|12|=
;
=
;
|-7.5|=
;
|0|=
.
12
3
5
7.5
0
绝对值一定是一个非负数.
如果a表示一个数,则|a|等于多少?
一般地,如果a表示一个数,则
(1)当a是正数时,|a|=a;
(2)当a=0时,|a|=0;
(3)当a是负数时,|a|=-a.
即|a|是指a和-a中非负数的那一个.
例6
若|a|=8.7,求a.
解
因为绝对值等于8.7的有理数有8.7和-8.7两个,所以a=8.7或a=-8.7.
练习
1.求下列各数的绝对值:
3,3.14,
,-2.8.
3
1
5
3.14
2.8
解
|3|=
;
|3.14|
=
;
=
;
|-2.8|=
.
2.填空:
-|-2018|=
;
-|-2.8|=
;
=
.
2018
-2.8
5
8
3.画一条数轴,并标出表示绝对值等于2,3.5的数的点.
解
绝对值等于2的数有2和-2,在数轴上分别用点A和点B表示;绝对值等于3.5的数有3.5和-3.5,分别用点C和点D表示.如下图:
O
0
-1
-2
-3
-4
-5
1
2
3
4
5
A
B
C
D
交流反思:
这节课你学到了哪些知识?
我学到了:绝对值一定是一个非负数.
我学到了求一个数的绝对值的方法:
|a|=
a
(a为正数时)
0
(a=0时)
-a
(a为负数时)
同学们积极投入学习,收获多多,每人获奖状一张.
作业
习题1.2第6、7、8、12题。
同课章节目录
