华东师大版九年级下册数学 27.1.3圆周角 同步习题(word版,含答案)
文档属性
| 名称 | 华东师大版九年级下册数学 27.1.3圆周角 同步习题(word版,含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 198.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-17 00:00:00 | ||
图片预览


文档简介
27.1.3圆周角
同步习题
一.选择题
1.如图,AB是圆O的直径,点C是半圆O上不同于A,B的一点,点D为弧AC的中点,连结OD,BD,AC,设∠CAB=β,∠BDO=α,则( )
A.α=β
B.α+2β=90°
C.2α+β=90°
D.α+β=45°
2.如图,在菱形ABCD中,∠A=60°,AB=3,⊙A,⊙B的半径分别为2和1,P,E,F分别是CD边、⊙A和⊙B上的动点,则PE+PF的最小值是( )
A.
B.2
C.3
D.3
3.如图,点A,B,C,D四点均在⊙O上,∠AOD=68°,AO∥DC,则∠B的度数为( )
A.40°
B.60°
C.56°
D.68°
4.如图,点A,B,C,D在圆O,AC是圆O的直径,∠CAD=26°,则∠ABD的度数为( )
A.26°
B.52°
C.64°
D.74°
5.已知:如图,⊙O的两条弦AE、BC相交于点D,连接AC、BE,若∠ACB=50°,则下列结论中正确的是( )
A.∠AOB=50°
B.∠ADB=50°
C.∠AEB=30°
D.∠AEB=50°
6.如图,四边形ABCD为⊙O的内接四边形,∠AOD+∠BOC=180°.若AD=2,BC=6,则△BOC的面积为( )
A.3
B.6
C.9
D.12
7.半径为2的⊙O中,两条弦AB=2,AC=2,∠BAC的度数为( )
A.45°或60°
B.105°
C.15°
D.15°或105°
8.如图,⊙O的直径AB过弦CD的中点E,∠COB=40°,则∠BAD等于( )
A.80°
B.50°
C.40°
D.20°
9.如图,AB是⊙O的弦,OC⊥AB交⊙O于点C,点D是⊙O上一点,∠ADC=25°,则∠BOC的度数为( )
A.30°
B.40°
C.50°
D.60°
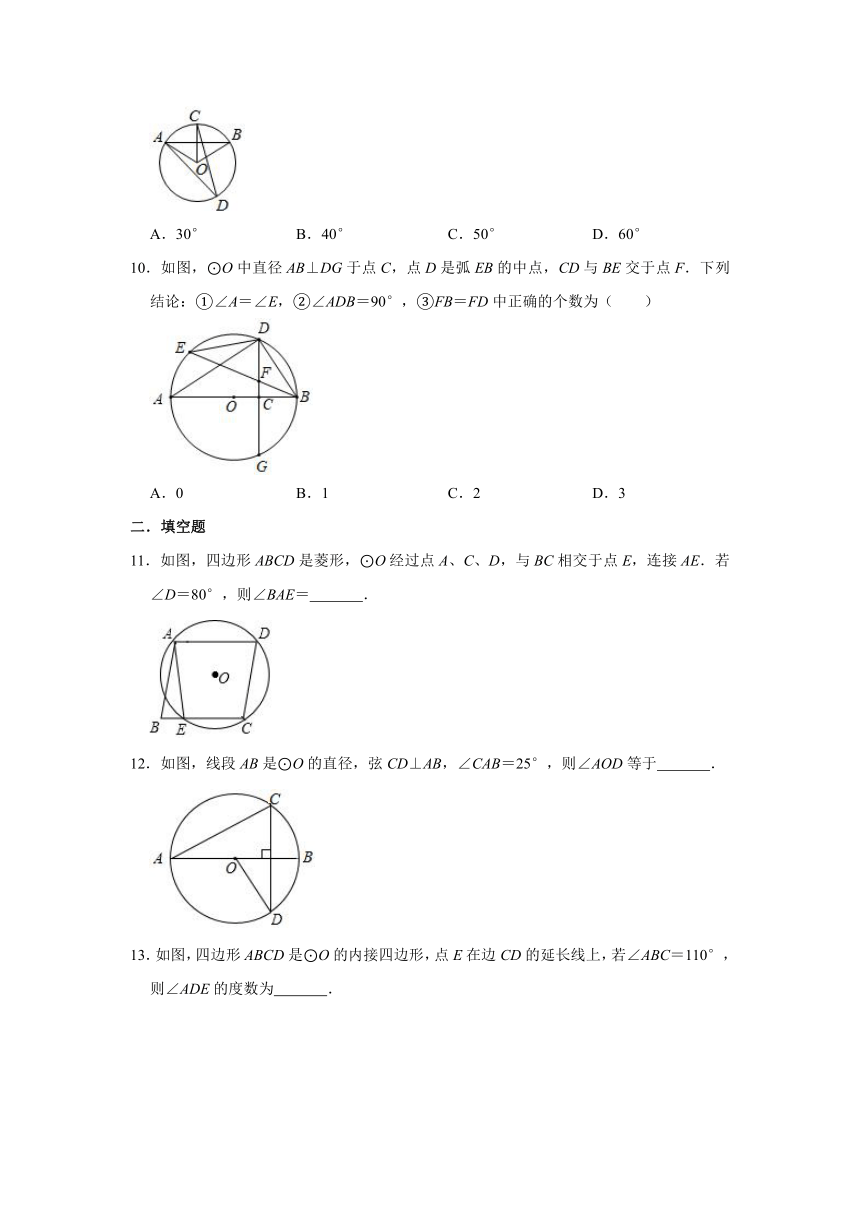
10.如图,⊙O中直径AB⊥DG于点C,点D是弧EB的中点,CD与BE交于点F.下列结论:①∠A=∠E,②∠ADB=90°,③FB=FD中正确的个数为( )
A.0
B.1
C.2
D.3
二.填空题
11.如图,四边形ABCD是菱形,⊙O经过点A、C、D,与BC相交于点E,连接AE.若∠D=80°,则∠BAE=
.
12.如图,线段AB是⊙O的直径,弦CD⊥AB,∠CAB=25°,则∠AOD等于
.
13.如图,四边形ABCD是⊙O的内接四边形,点E在边CD的延长线上,若∠ABC=110°,则∠ADE的度数为
.
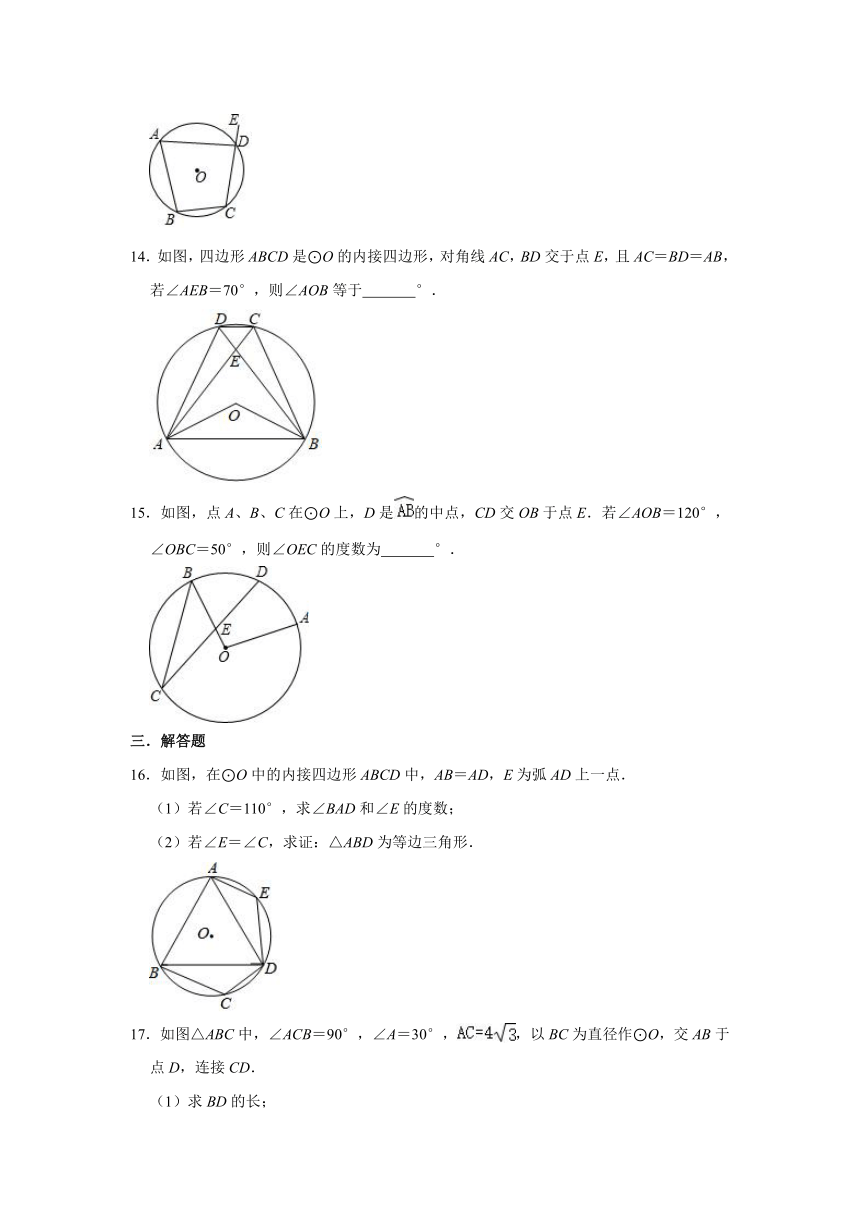
14.如图,四边形ABCD是⊙O的内接四边形,对角线AC,BD交于点E,且AC=BD=AB,若∠AEB=70°,则∠AOB等于
°.
15.如图,点A、B、C在⊙O上,D是的中点,CD交OB于点E.若∠AOB=120°,∠OBC=50°,则∠OEC的度数为
°.
三.解答题
16.如图,在⊙O中的内接四边形ABCD中,AB=AD,E为弧AD上一点.
(1)若∠C=110°,求∠BAD和∠E的度数;
(2)若∠E=∠C,求证:△ABD为等边三角形.
17.如图△ABC中,∠ACB=90°,∠A=30°,,以BC为直径作⊙O,交AB于点D,连接CD.
(1)求BD的长;
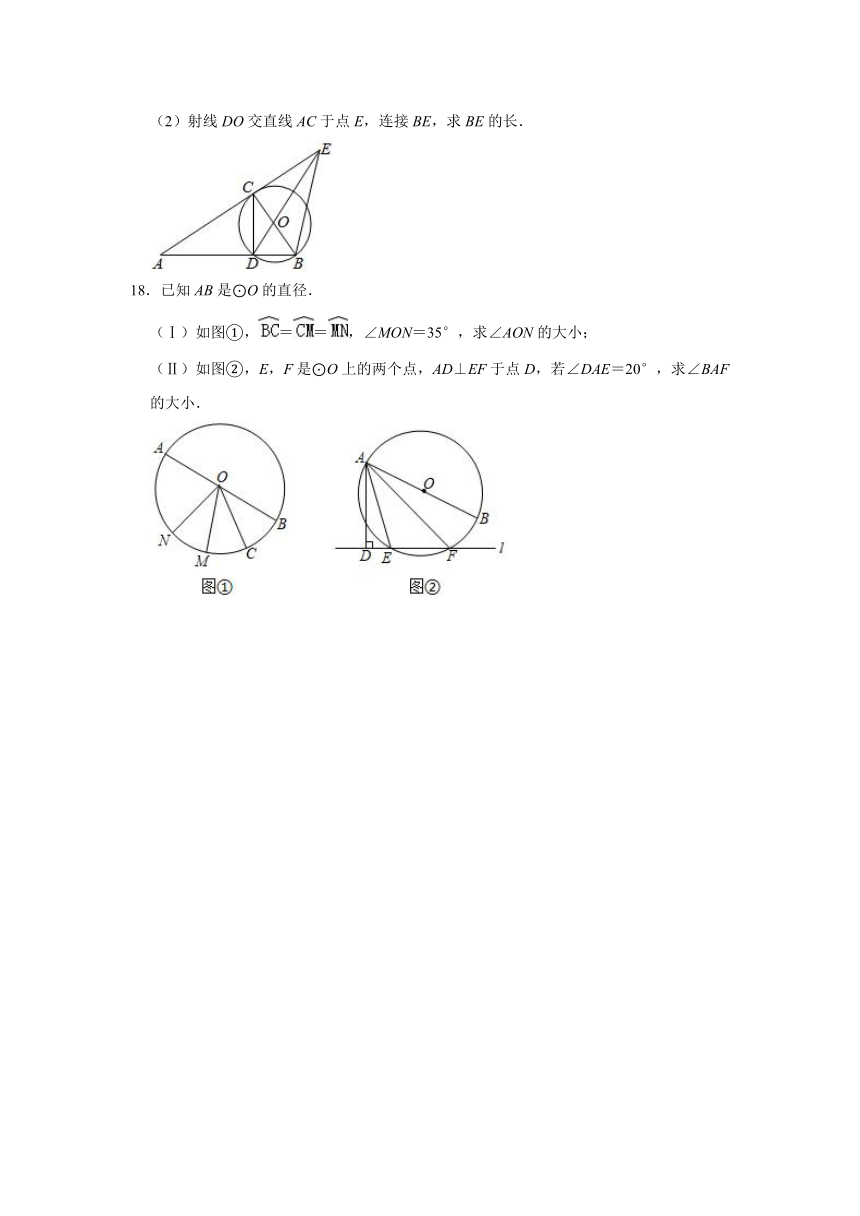
(2)射线DO交直线AC于点E,连接BE,求BE的长.
18.已知AB是⊙O的直径.
(Ⅰ)如图①,==,∠MON=35°,求∠AON的大小;
(Ⅱ)如图②,E,F是⊙O上的两个点,AD⊥EF于点D,若∠DAE=20°,求∠BAF的大小.
参考答案
一.选择题
1.解:如图,设AC与DO交点为E,如图,
∵OD=OB,
∴∠OBD=∠BDO=α,
∴∠DOA=2∠OBD=2α,
又∵D为中点,AB为⊙O直径,
∴OD⊥AC,
∴∠EAO+∠EOA=90°,
即2α+β=90°.
故选:C.
2.解:作A点关于直线DC的对称点A′,连接BD,DA′,
∵四边形ABCD是菱形,
∴AB=AD,
∵∠BDA=60°,
∴△ADB是等边三角形,
∴∠ADB=60°,
∵∠BDC=∠ADB=60°,
∴∠ADN=60°,
∴∠A′DN=60°,
∴∠ADB+∠ADA′=180°,
∴A′,D,B在一条直线上,
由题意可得出:此时P与D重合,E点在AD上,F在BD上,此时PE+PF最小,
∵菱形ABCD中,∠A=60°,
∴AB=AD,则△ABD是等边三角形,
∴BD=AB=AD=3,
∵⊙A、⊙B的半径分别为2和1,
∴PE=1,DF=2,
∴PE+PF的最小值是3.
故选:C.
3.解:如图,
连接OC,
∵AO∥DC,
∴∠ODC=∠AOD=68°,
∵OD=OC,
∴∠ODC=∠OCD=68°,
∴∠COD=34°,
∴∠AOC=112°,
∴∠B=∠AOC=56°.
故选:C.
4.解:∵AC是⊙O的直径,
∴∠ADC=90°,
∴∠ACD=90°﹣∠CAD=90°﹣26°=64°,
∴∠ABD=∠ACD=64°.
故选:C.
5.解:∵∠ACB=50°,
∴∠AEB=∠ACB=50°,∠AOB=2∠ACB=100°,
∠ADB=∠ACB+∠CAD>∠ACB=50°,
故选项A、B、C不正确,只有选项D正确,
故选:D.
6.解:延长BO交⊙O于E,连接CE,
则∠COE+∠BOC=180°,∠BCE=90°,
即CE⊥BC,
∵∠AOD+∠BOC=180°,
∴∠AOD=∠COE,
∴=,
∴AD=CE=2,
∵BC=6,
∴△BEC的面积为BC?CE=×6×2=6,
∵OB=OE,
∴△BOC的面积=△BEC的面积=×6=3,
故选:A.
7.解:分为两种情况:①如图,弦AB和弦AC在直径AE的同旁时,
过O作OG⊥AB于G,OF⊥AC于F,
∵OG和OF都过圆心O,OG⊥AB,OF⊥AC,AB=2,AC=2,
∴AG=AB=,AF=AC=1=AO,∠AGO=∠AFO=90°,
∴∠FOA=30°,OG====AG,
∴∠FAO=60°,∠GAO=45°,
∴∠BAC=∠FAO﹣∠GAO=60°﹣45°=15°;
②当弦AC和弦AB在直径AE的两旁时,
此时∠BAC=∠GAO+∠FAO=60°+45°=105°;
所以∠BAC的度数是15°或105°,
故选:D.
8.解:∵直径AB过弦CD的中点E,
∴AB⊥CD,
∴=,
∴∠BAD=∠COB=×40°=20°.
故选:D.
9.解:∵OC⊥AB,
∴,
∴∠AOC=∠BOC,
∵∠ADC=25°,
∴∠AOC=50°,
∴∠BOC=50°,
故选:C.
10.解:∵∠A与∠E都对,
∴∠A=∠E,所以①正确;
∵AB为直径,
∴∠ADB=90°,所以②正确;
∵AB⊥DG,
∴=,
∵点D是弧EB的中点,
即=,
∴=,
∴∠DBE=∠BDG,
∴FB=FD,所以③正确.
故选:D.
二.填空题
11.解:∵四边形ABCD是菱形,
∴∠B=∠D=80°,
∵∠D+∠AEC=180°,
∴∠AEC=180°﹣80°=100°,
∵∠AEC=∠B+∠BAE,
∴∠BAE=∠AEC﹣∠B=100°﹣80°=20°.
故答案为20°.
12.解:连接BD,如图,
∵CD⊥AB,
∴∠C=90°﹣∠CAB=90°﹣25°=65°,
∴∠B=∠C=65°,
∴∠AOD=2∠B=130°.
故答案为130°.
13.解:∵四边形ABCD是⊙O的内接四边形,
∴∠ADE=∠ABC=110°,
故答案为:110°.
14.解:延长AO交BC于点G,延长BO交AD于点H,
∵AC=AB,
∴=,
∴AG⊥BC,BG=CG,
∴∠CAO=∠BAO,
∵BD=AB,
∴=,
∴BH⊥AD,AH=DH,
∴∠ABO=∠DBO,
∵∠AEB=70°,
∴∠ABO+∠OAB=(∠EAB+∠EBA)=(180°﹣70°)=55°,
∴∠AOB=180°﹣55°=125°.
故答案为:125.
15.解:连接OD,
∵D是的中点,∠AOB=120°,
∴∠BOD=∠AOD=∠AOB=60°,
由圆周角定理得,∠BCD=∠BOD=30°,
∴∠OEC=∠BCD+∠OBC=80°,
故答案为:80.
三.解答题
16.解:(1)∵四边形ABCD内接于⊙O,
∴∠BAD+∠C=180°,
∵∠C=110°,
∴∠BAD=70°,
∵AB=AD,
∴∠ABD=∠ADB=55°,
∵四边形ABDE内接于⊙O,
∴∠ABD+∠E=180°,
∴∠E=125°.
(2)∵四边形ABCD是⊙O的内接四边形,
∴∠BAD+∠C=180°,
∵四边形ABDE是⊙O的内接四边形,
∴∠ABD+∠E=180°,
又∵∠E=∠C,
∴∠BAD=∠ABD,
∴AD=BD,
∵AB=AD,
∴AD=BD=AD,
∴△ABD为等边三角形.
17.解:(1)∵∠ACB=90°,∠A=30°,
∴AB=2BC,∠ABC=60°,
∵,AC2+BC2=AB2,
∴(4)2+BC2=(2BC)2,
∴BC=4,
∵BC为直径,
∴∠CDB=90°,
∴∠DCB=∠A=30°,
∴BD=BC=2;
(2)∵OD=OB,
∴∠CBD=∠EDB=60°,
∴∠DOB=180°﹣60°﹣60°=60°,
∴∠COE=∠DOB=60°,
∵∠OCE=180°﹣∠ACB=180°﹣90°=90°,
∴∠CEO=30°,
∵OC=OB=BC==2,
∴OE=2CO=4,
∴CE===2,
∴BE===2.
18.解:(I)∵==,∠MON=35°,
∴∠MON=∠MOC=∠BOC=35°,
∴∠AON=180°﹣∠MON﹣∠MOC﹣∠BOC=180°﹣35°﹣35°﹣35°=75°;
(II)连接BF,
∵AD⊥直线l,
∴∠ADE=90°,
∵∠DAE=20°,
∴∠AEF=∠ADE+∠DAE=110°,
∵A、E、F、B四点共圆,
∴∠ABF+∠AEF=180°,
∴∠ABF=70°,
∵AB是⊙O的直径,
∴∠AFB=90°,
∴∠BAF=180°﹣∠AFB﹣∠ABF=20°.
同步习题
一.选择题
1.如图,AB是圆O的直径,点C是半圆O上不同于A,B的一点,点D为弧AC的中点,连结OD,BD,AC,设∠CAB=β,∠BDO=α,则( )
A.α=β
B.α+2β=90°
C.2α+β=90°
D.α+β=45°
2.如图,在菱形ABCD中,∠A=60°,AB=3,⊙A,⊙B的半径分别为2和1,P,E,F分别是CD边、⊙A和⊙B上的动点,则PE+PF的最小值是( )
A.
B.2
C.3
D.3
3.如图,点A,B,C,D四点均在⊙O上,∠AOD=68°,AO∥DC,则∠B的度数为( )
A.40°
B.60°
C.56°
D.68°
4.如图,点A,B,C,D在圆O,AC是圆O的直径,∠CAD=26°,则∠ABD的度数为( )
A.26°
B.52°
C.64°
D.74°
5.已知:如图,⊙O的两条弦AE、BC相交于点D,连接AC、BE,若∠ACB=50°,则下列结论中正确的是( )
A.∠AOB=50°
B.∠ADB=50°
C.∠AEB=30°
D.∠AEB=50°
6.如图,四边形ABCD为⊙O的内接四边形,∠AOD+∠BOC=180°.若AD=2,BC=6,则△BOC的面积为( )
A.3
B.6
C.9
D.12
7.半径为2的⊙O中,两条弦AB=2,AC=2,∠BAC的度数为( )
A.45°或60°
B.105°
C.15°
D.15°或105°
8.如图,⊙O的直径AB过弦CD的中点E,∠COB=40°,则∠BAD等于( )
A.80°
B.50°
C.40°
D.20°
9.如图,AB是⊙O的弦,OC⊥AB交⊙O于点C,点D是⊙O上一点,∠ADC=25°,则∠BOC的度数为( )
A.30°
B.40°
C.50°
D.60°
10.如图,⊙O中直径AB⊥DG于点C,点D是弧EB的中点,CD与BE交于点F.下列结论:①∠A=∠E,②∠ADB=90°,③FB=FD中正确的个数为( )
A.0
B.1
C.2
D.3
二.填空题
11.如图,四边形ABCD是菱形,⊙O经过点A、C、D,与BC相交于点E,连接AE.若∠D=80°,则∠BAE=
.
12.如图,线段AB是⊙O的直径,弦CD⊥AB,∠CAB=25°,则∠AOD等于
.
13.如图,四边形ABCD是⊙O的内接四边形,点E在边CD的延长线上,若∠ABC=110°,则∠ADE的度数为
.
14.如图,四边形ABCD是⊙O的内接四边形,对角线AC,BD交于点E,且AC=BD=AB,若∠AEB=70°,则∠AOB等于
°.
15.如图,点A、B、C在⊙O上,D是的中点,CD交OB于点E.若∠AOB=120°,∠OBC=50°,则∠OEC的度数为
°.
三.解答题
16.如图,在⊙O中的内接四边形ABCD中,AB=AD,E为弧AD上一点.
(1)若∠C=110°,求∠BAD和∠E的度数;
(2)若∠E=∠C,求证:△ABD为等边三角形.
17.如图△ABC中,∠ACB=90°,∠A=30°,,以BC为直径作⊙O,交AB于点D,连接CD.
(1)求BD的长;
(2)射线DO交直线AC于点E,连接BE,求BE的长.
18.已知AB是⊙O的直径.
(Ⅰ)如图①,==,∠MON=35°,求∠AON的大小;
(Ⅱ)如图②,E,F是⊙O上的两个点,AD⊥EF于点D,若∠DAE=20°,求∠BAF的大小.
参考答案
一.选择题
1.解:如图,设AC与DO交点为E,如图,
∵OD=OB,
∴∠OBD=∠BDO=α,
∴∠DOA=2∠OBD=2α,
又∵D为中点,AB为⊙O直径,
∴OD⊥AC,
∴∠EAO+∠EOA=90°,
即2α+β=90°.
故选:C.
2.解:作A点关于直线DC的对称点A′,连接BD,DA′,
∵四边形ABCD是菱形,
∴AB=AD,
∵∠BDA=60°,
∴△ADB是等边三角形,
∴∠ADB=60°,
∵∠BDC=∠ADB=60°,
∴∠ADN=60°,
∴∠A′DN=60°,
∴∠ADB+∠ADA′=180°,
∴A′,D,B在一条直线上,
由题意可得出:此时P与D重合,E点在AD上,F在BD上,此时PE+PF最小,
∵菱形ABCD中,∠A=60°,
∴AB=AD,则△ABD是等边三角形,
∴BD=AB=AD=3,
∵⊙A、⊙B的半径分别为2和1,
∴PE=1,DF=2,
∴PE+PF的最小值是3.
故选:C.
3.解:如图,
连接OC,
∵AO∥DC,
∴∠ODC=∠AOD=68°,
∵OD=OC,
∴∠ODC=∠OCD=68°,
∴∠COD=34°,
∴∠AOC=112°,
∴∠B=∠AOC=56°.
故选:C.
4.解:∵AC是⊙O的直径,
∴∠ADC=90°,
∴∠ACD=90°﹣∠CAD=90°﹣26°=64°,
∴∠ABD=∠ACD=64°.
故选:C.
5.解:∵∠ACB=50°,
∴∠AEB=∠ACB=50°,∠AOB=2∠ACB=100°,
∠ADB=∠ACB+∠CAD>∠ACB=50°,
故选项A、B、C不正确,只有选项D正确,
故选:D.
6.解:延长BO交⊙O于E,连接CE,
则∠COE+∠BOC=180°,∠BCE=90°,
即CE⊥BC,
∵∠AOD+∠BOC=180°,
∴∠AOD=∠COE,
∴=,
∴AD=CE=2,
∵BC=6,
∴△BEC的面积为BC?CE=×6×2=6,
∵OB=OE,
∴△BOC的面积=△BEC的面积=×6=3,
故选:A.
7.解:分为两种情况:①如图,弦AB和弦AC在直径AE的同旁时,
过O作OG⊥AB于G,OF⊥AC于F,
∵OG和OF都过圆心O,OG⊥AB,OF⊥AC,AB=2,AC=2,
∴AG=AB=,AF=AC=1=AO,∠AGO=∠AFO=90°,
∴∠FOA=30°,OG====AG,
∴∠FAO=60°,∠GAO=45°,
∴∠BAC=∠FAO﹣∠GAO=60°﹣45°=15°;
②当弦AC和弦AB在直径AE的两旁时,
此时∠BAC=∠GAO+∠FAO=60°+45°=105°;
所以∠BAC的度数是15°或105°,
故选:D.
8.解:∵直径AB过弦CD的中点E,
∴AB⊥CD,
∴=,
∴∠BAD=∠COB=×40°=20°.
故选:D.
9.解:∵OC⊥AB,
∴,
∴∠AOC=∠BOC,
∵∠ADC=25°,
∴∠AOC=50°,
∴∠BOC=50°,
故选:C.
10.解:∵∠A与∠E都对,
∴∠A=∠E,所以①正确;
∵AB为直径,
∴∠ADB=90°,所以②正确;
∵AB⊥DG,
∴=,
∵点D是弧EB的中点,
即=,
∴=,
∴∠DBE=∠BDG,
∴FB=FD,所以③正确.
故选:D.
二.填空题
11.解:∵四边形ABCD是菱形,
∴∠B=∠D=80°,
∵∠D+∠AEC=180°,
∴∠AEC=180°﹣80°=100°,
∵∠AEC=∠B+∠BAE,
∴∠BAE=∠AEC﹣∠B=100°﹣80°=20°.
故答案为20°.
12.解:连接BD,如图,
∵CD⊥AB,
∴∠C=90°﹣∠CAB=90°﹣25°=65°,
∴∠B=∠C=65°,
∴∠AOD=2∠B=130°.
故答案为130°.
13.解:∵四边形ABCD是⊙O的内接四边形,
∴∠ADE=∠ABC=110°,
故答案为:110°.
14.解:延长AO交BC于点G,延长BO交AD于点H,
∵AC=AB,
∴=,
∴AG⊥BC,BG=CG,
∴∠CAO=∠BAO,
∵BD=AB,
∴=,
∴BH⊥AD,AH=DH,
∴∠ABO=∠DBO,
∵∠AEB=70°,
∴∠ABO+∠OAB=(∠EAB+∠EBA)=(180°﹣70°)=55°,
∴∠AOB=180°﹣55°=125°.
故答案为:125.
15.解:连接OD,
∵D是的中点,∠AOB=120°,
∴∠BOD=∠AOD=∠AOB=60°,
由圆周角定理得,∠BCD=∠BOD=30°,
∴∠OEC=∠BCD+∠OBC=80°,
故答案为:80.
三.解答题
16.解:(1)∵四边形ABCD内接于⊙O,
∴∠BAD+∠C=180°,
∵∠C=110°,
∴∠BAD=70°,
∵AB=AD,
∴∠ABD=∠ADB=55°,
∵四边形ABDE内接于⊙O,
∴∠ABD+∠E=180°,
∴∠E=125°.
(2)∵四边形ABCD是⊙O的内接四边形,
∴∠BAD+∠C=180°,
∵四边形ABDE是⊙O的内接四边形,
∴∠ABD+∠E=180°,
又∵∠E=∠C,
∴∠BAD=∠ABD,
∴AD=BD,
∵AB=AD,
∴AD=BD=AD,
∴△ABD为等边三角形.
17.解:(1)∵∠ACB=90°,∠A=30°,
∴AB=2BC,∠ABC=60°,
∵,AC2+BC2=AB2,
∴(4)2+BC2=(2BC)2,
∴BC=4,
∵BC为直径,
∴∠CDB=90°,
∴∠DCB=∠A=30°,
∴BD=BC=2;
(2)∵OD=OB,
∴∠CBD=∠EDB=60°,
∴∠DOB=180°﹣60°﹣60°=60°,
∴∠COE=∠DOB=60°,
∵∠OCE=180°﹣∠ACB=180°﹣90°=90°,
∴∠CEO=30°,
∵OC=OB=BC==2,
∴OE=2CO=4,
∴CE===2,
∴BE===2.
18.解:(I)∵==,∠MON=35°,
∴∠MON=∠MOC=∠BOC=35°,
∴∠AON=180°﹣∠MON﹣∠MOC﹣∠BOC=180°﹣35°﹣35°﹣35°=75°;
(II)连接BF,
∵AD⊥直线l,
∴∠ADE=90°,
∵∠DAE=20°,
∴∠AEF=∠ADE+∠DAE=110°,
∵A、E、F、B四点共圆,
∴∠ABF+∠AEF=180°,
∴∠ABF=70°,
∵AB是⊙O的直径,
∴∠AFB=90°,
∴∠BAF=180°﹣∠AFB﹣∠ABF=20°.
