人教版(五四制)七年级数学上册期末复习试题(word版含解析)
文档属性
| 名称 | 人教版(五四制)七年级数学上册期末复习试题(word版含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 76.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-17 00:00:00 | ||
图片预览




文档简介
七年级数学上册期末复习试题
(满分120分;时间:120分钟)
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
1.
下列关于方程的说法中,错误的是(????????)
A.方程是等式
B.等式是方程
C.等式的性质是解方程的基本依据
D.使方程等号左右两边相等的未知数的值是方程的解
?
2.
下列说法不正确的是?
?
?
?
A.如果,那么
B.如果,那么
C.如果,那么
D.如果,那么
?
3.
若是关于的一元一次方程,则的值(
)
A.
B.
C.
D.
?
4.
下列结论中正确的是(
)
A.在等式的两边都除以,可得等式
B.如果,那么
C.在等式的两边都除以,可得等式
D.在等式的两边都减去,可得等式
?
5.
下列式子中,正确的是(?
?
?
?
)
A.
B.
C.
D.
?
6.
解方程时,去分母后可以得到?
?
?
?
A.
B.
C.
D.
?7.
下列命题中,错误的是(
)
A.对顶角的角平分线互为反向延长线
B.在同一平面内,垂直于同一直线的两条直线互相平行
C.如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补
D.同时垂直于两条平行线,并且夹在这两条平行线间的线段叫做这两条平行线的距离
?
8.
若且,则
A.
B.
C.
D.
?
9.
已知,则的值为(
)
A.
B.
C.
D.
?
10.
已知方程有一个负根而且没有正根,那么的取值范围是(
)
A.
B.
C.
D.非上述答案
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?
11.
已知关于的方程和方程的解相同,则________.
?
12.
已知的平方根是,则的立方根是________.
?
13.
已知与互为相反数,则可列方程________.
?
14.
一个两位数,个位上的数字是十位上数字的倍,它们的和是,那么这个两位数是________.
?
15.
的相反数是________;的绝对值是________.
?
16.
小明和小彬每天坚持跑步,小明每秒跑米,小彬每秒跑米,如果他们同时从相距米的两地相向起跑,那么几秒后两人相遇?若设秒后两人相遇,可列方程________.
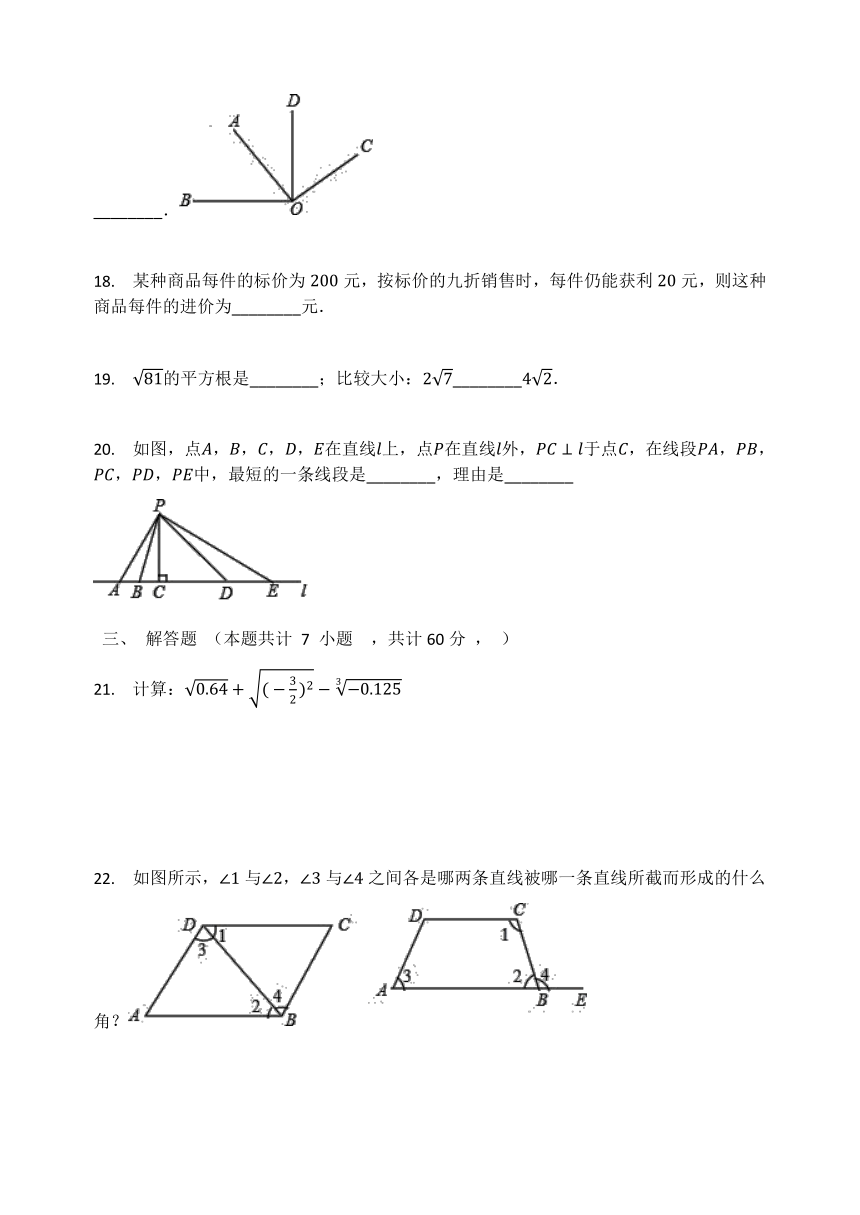
?17.
如图,若,,且,则等于________.
?
18.
某种商品每件的标价为元,按标价的九折销售时,每件仍能获利元,则这种商品每件的进价为________元.
?
19.
的平方根是________;比较大小:________.
?
20.
如图,点,,,,在直线上,点在直线外,于点,在线段,,,,中,最短的一条线段是________,理由是________
三、
解答题
(本题共计
7
小题
,共计60分
,
)
?
21.
计算:
?
22.
如图所示,与,与之间各是哪两条直线被哪一条直线所截而形成的什么角?
?
23.
如图,正方形的边长为,过它的中心建立平面直角坐标系(中心在原点上),各边和坐标轴平行或垂直.
试写出正方形四个顶点的坐标;
从中你发现了什么规律,请举例说明(写出一个即可).
?
24.
如图,已知,直线与、相交于、两点,平分.
(1)若=,求和的度数;
(2)若=,请直接写出和的度数.
?
25.
如图,房子的地基长为米,房檐的长为米,门宽为米,到地面的距离为米,请你建立直角坐标系并直接写出,,,,,的坐标.
?
26.
现有四个整式:,,,.
若选择其中两个整式用等号连接,则共能组成________个方程;
请列出中所有的一元一次方程,并解方程.
?
27.
如图,已知边长为的正方形在平面直角坐标系中,,两点在第二象限内,与轴的夹角为,那么点坐标为多少?点坐标为多少?
参考答案
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
1.
【答案】
B
【解答】
解:含有未知数的等式叫作方程,所以方程一定是等式,等式却不一定是方程,故正确,错误;
解方程的基本依据是等式的性质,故正确;
使方程等号左右两边相等的未知数的值是方程的解,故正确.
故选.
2.
【答案】
B
【解答】
解:,根据等式性质,两边都减,即可得到,故本选项正确;
,根据等式性质,当时,两边同时除以,即可得到,故本选项错误;
,根据等式性质,两边都乘以,即可得到,故本选项正确;
,根据等式性质,因为在分母上,所以,两边都乘以,即可得到,故本选项正确.
故选.
3.
【答案】
C
【解答】
解:由一元一次方程的特点得,
解得:.
故选:.
4.
【答案】
B
【解答】
解:、根据等式性质,在等式的两边都除以,可得等式;
、根据等式的对称性可得;
、根据等式的性质,在等式的两边都除以,可得等式;
、根据等式性质,在等式的两边都减去,可得等式;
综上所述,故选.
5.
【答案】
A
【解答】
解:、,故正确;
、,故错误;
、,故错误;
、,故错误.
故选.
6.
【答案】
B
【解答】
解:方程两边乘以得:,
去括号得:,
故选.
7.
【答案】
D
【解答】
解:、对顶角的角平分线成的角,它们互为反向延长,所以选项的说法正确;
、在同一平面内,垂直于同一直线的两条直线互相平行,所以选项的说法正确;
、如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补,所以选项的说法正确;
、同时垂直于两条平行线,并且夹在这两条平行线间的线段长叫做这两条平行线的距离,所以选项的说法错误.
故选.
8.
【答案】
C
【解答】
解:根据题意设,,,
代入中得:,即,
则,
故选.
9.
【答案】
D
【解答】
解:依题意得:,
∴
,
则.
故选.
10.
【答案】
A
【解答】
解:如果,,
,
,
,
.
故选.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
)
11.
【答案】
【解答】
解:由题意可得:,
解得:,
故答案为:
12.
【答案】
【解答】
∵
的平方根是,
∴
=,
∴
=,
∴
=,
∴
的立方根是,
13.
【答案】
【解答】
解:∵
与互为相反数,
∴
.
故答案为:.
14.
【答案】
【解答】
解:设十位上的数字是,则个位上的数字是.
则
解得:
所以该数为:.
15.
【答案】
,
【解答】
解:的相反数是;
的绝对值是.
故答案为:;.
16.
【答案】
【解答】
解:设秒后两人相遇,
则得出小明在秒中所跑路程为米,小彬所跑路程为米,
根据等量关系小明跑的路程小彬跑的路程两地的距离,
可以得出.
故答案为:.
17.
【答案】
【解答】
解:∵
,,
∴
,
∴
,
∵
,
∴
,
∴
,
∴
,
故答案为:.
18.
【答案】
【解答】
解:设这种商品每件的进价为元,
则:,
解得:.
故答案为:.
19.
【答案】
,
【解答】
解:的平方根是;
,,
∵
,
∴
.
故答案为:;.
20.
【答案】
,垂线段最短
【解答】
根据点到直线的距离的定义得出线段的长是点到直线的距离,从直线外一点到这条直线所作的垂线段最短.
三、
解答题
(本题共计
7
小题
,每题
10
分
,共计70分
)
21.
【答案】
原式=
=.
【解答】
原式=
=.
22.
【答案】
解:左图:与是与被直线所截形成的内错角,
与是直线与直线被直线所截形成的内错角;
右图:与是与被直线所截形成的同旁内角,
与是直线与直线被直线所截形成的同位角.
【解答】
解:左图:与是与被直线所截形成的内错角,
与是直线与直线被直线所截形成的内错角;
右图:与是与被直线所截形成的同旁内角,
与是直线与直线被直线所截形成的同位角.
23.
【答案】
解:设正方形与轴的交点分别为,(点在点下方),
与轴交于、点(点在点右方),如图所示:
∵
正方形的边长为,且中心为坐标原点,
∴
,
∴
点的坐标为,点的坐标为,点的坐标为,点的坐标为.
,点的横(纵)坐标互为相反数.
连接,,如图所示:
∵
坐标原点为正方形的中心,且正方形的对角线互相平分,
∴
点为线段的中点,
∴
,点的横(纵)坐标互为相反数.
【解答】
解:设正方形与轴的交点分别为,(点在点下方),
与轴交于、点(点在点右方),如图所示:
∵
正方形的边长为,且中心为坐标原点,
∴
,
∴
点的坐标为,点的坐标为,点的坐标为,点的坐标为.
,点的横(纵)坐标互为相反数.
连接,,如图所示:
∵
坐标原点为正方形的中心,且正方形的对角线互相平分,
∴
点为线段的中点,
∴
,点的横(纵)坐标互为相反数.
24.
【答案】
∵
=,=,
∴
=,
又∵
,
∴
=,=
∴
=,
又∵
平分,
∴
=,
∴
=;
若=时,
同理可得:
=;
=
【解答】
∵
=,=,
∴
=,
又∵
,
∴
=,=
∴
=,
又∵
平分,
∴
=,
∴
=;
若=时,
同理可得:
=;
=
25.
【答案】
解:建立平面直角坐标系如图所示,
,,,,,.
【解答】
解:建立平面直角坐标系如图所示,
,,,,,.
26.
【答案】
,
去分母得:,
解得:;
,
去分母得:,
解得:.
【解答】
解:根据方程的定义,若选择其中两个整式用等号连接,则共能组成个方程.
故答案为:.
(2),
去分母得:,
解得:;
,
去分母得:,
解得:.
27.
【答案】
解:如图,∵
与轴的夹角为,四边形为正方形,
∴
,
∴
,
,
∵
点在第二象限,
∴
点的坐标为;
∵
与轴的夹角为,
∴
,
∴
,
,
∴
,
在中,,
∴
,
,
∴
,
∵
点在第二象限,
∴
点的坐标为.
【解答】
解:如图,∵
与轴的夹角为,四边形为正方形,
∴
,
∴
,
,
∵
点在第二象限,
∴
点的坐标为;
∵
与轴的夹角为,
∴
,
∴
,
,
∴
,
在中,,
∴
,
,
∴
,
∵
点在第二象限,
∴
点的坐标为.
.
(满分120分;时间:120分钟)
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
1.
下列关于方程的说法中,错误的是(????????)
A.方程是等式
B.等式是方程
C.等式的性质是解方程的基本依据
D.使方程等号左右两边相等的未知数的值是方程的解
?
2.
下列说法不正确的是?
?
?
?
A.如果,那么
B.如果,那么
C.如果,那么
D.如果,那么
?
3.
若是关于的一元一次方程,则的值(
)
A.
B.
C.
D.
?
4.
下列结论中正确的是(
)
A.在等式的两边都除以,可得等式
B.如果,那么
C.在等式的两边都除以,可得等式
D.在等式的两边都减去,可得等式
?
5.
下列式子中,正确的是(?
?
?
?
)
A.
B.
C.
D.
?
6.
解方程时,去分母后可以得到?
?
?
?
A.
B.
C.
D.
?7.
下列命题中,错误的是(
)
A.对顶角的角平分线互为反向延长线
B.在同一平面内,垂直于同一直线的两条直线互相平行
C.如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补
D.同时垂直于两条平行线,并且夹在这两条平行线间的线段叫做这两条平行线的距离
?
8.
若且,则
A.
B.
C.
D.
?
9.
已知,则的值为(
)
A.
B.
C.
D.
?
10.
已知方程有一个负根而且没有正根,那么的取值范围是(
)
A.
B.
C.
D.非上述答案
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?
11.
已知关于的方程和方程的解相同,则________.
?
12.
已知的平方根是,则的立方根是________.
?
13.
已知与互为相反数,则可列方程________.
?
14.
一个两位数,个位上的数字是十位上数字的倍,它们的和是,那么这个两位数是________.
?
15.
的相反数是________;的绝对值是________.
?
16.
小明和小彬每天坚持跑步,小明每秒跑米,小彬每秒跑米,如果他们同时从相距米的两地相向起跑,那么几秒后两人相遇?若设秒后两人相遇,可列方程________.
?17.
如图,若,,且,则等于________.
?
18.
某种商品每件的标价为元,按标价的九折销售时,每件仍能获利元,则这种商品每件的进价为________元.
?
19.
的平方根是________;比较大小:________.
?
20.
如图,点,,,,在直线上,点在直线外,于点,在线段,,,,中,最短的一条线段是________,理由是________
三、
解答题
(本题共计
7
小题
,共计60分
,
)
?
21.
计算:
?
22.
如图所示,与,与之间各是哪两条直线被哪一条直线所截而形成的什么角?
?
23.
如图,正方形的边长为,过它的中心建立平面直角坐标系(中心在原点上),各边和坐标轴平行或垂直.
试写出正方形四个顶点的坐标;
从中你发现了什么规律,请举例说明(写出一个即可).
?
24.
如图,已知,直线与、相交于、两点,平分.
(1)若=,求和的度数;
(2)若=,请直接写出和的度数.
?
25.
如图,房子的地基长为米,房檐的长为米,门宽为米,到地面的距离为米,请你建立直角坐标系并直接写出,,,,,的坐标.
?
26.
现有四个整式:,,,.
若选择其中两个整式用等号连接,则共能组成________个方程;
请列出中所有的一元一次方程,并解方程.
?
27.
如图,已知边长为的正方形在平面直角坐标系中,,两点在第二象限内,与轴的夹角为,那么点坐标为多少?点坐标为多少?
参考答案
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
1.
【答案】
B
【解答】
解:含有未知数的等式叫作方程,所以方程一定是等式,等式却不一定是方程,故正确,错误;
解方程的基本依据是等式的性质,故正确;
使方程等号左右两边相等的未知数的值是方程的解,故正确.
故选.
2.
【答案】
B
【解答】
解:,根据等式性质,两边都减,即可得到,故本选项正确;
,根据等式性质,当时,两边同时除以,即可得到,故本选项错误;
,根据等式性质,两边都乘以,即可得到,故本选项正确;
,根据等式性质,因为在分母上,所以,两边都乘以,即可得到,故本选项正确.
故选.
3.
【答案】
C
【解答】
解:由一元一次方程的特点得,
解得:.
故选:.
4.
【答案】
B
【解答】
解:、根据等式性质,在等式的两边都除以,可得等式;
、根据等式的对称性可得;
、根据等式的性质,在等式的两边都除以,可得等式;
、根据等式性质,在等式的两边都减去,可得等式;
综上所述,故选.
5.
【答案】
A
【解答】
解:、,故正确;
、,故错误;
、,故错误;
、,故错误.
故选.
6.
【答案】
B
【解答】
解:方程两边乘以得:,
去括号得:,
故选.
7.
【答案】
D
【解答】
解:、对顶角的角平分线成的角,它们互为反向延长,所以选项的说法正确;
、在同一平面内,垂直于同一直线的两条直线互相平行,所以选项的说法正确;
、如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补,所以选项的说法正确;
、同时垂直于两条平行线,并且夹在这两条平行线间的线段长叫做这两条平行线的距离,所以选项的说法错误.
故选.
8.
【答案】
C
【解答】
解:根据题意设,,,
代入中得:,即,
则,
故选.
9.
【答案】
D
【解答】
解:依题意得:,
∴
,
则.
故选.
10.
【答案】
A
【解答】
解:如果,,
,
,
,
.
故选.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
)
11.
【答案】
【解答】
解:由题意可得:,
解得:,
故答案为:
12.
【答案】
【解答】
∵
的平方根是,
∴
=,
∴
=,
∴
=,
∴
的立方根是,
13.
【答案】
【解答】
解:∵
与互为相反数,
∴
.
故答案为:.
14.
【答案】
【解答】
解:设十位上的数字是,则个位上的数字是.
则
解得:
所以该数为:.
15.
【答案】
,
【解答】
解:的相反数是;
的绝对值是.
故答案为:;.
16.
【答案】
【解答】
解:设秒后两人相遇,
则得出小明在秒中所跑路程为米,小彬所跑路程为米,
根据等量关系小明跑的路程小彬跑的路程两地的距离,
可以得出.
故答案为:.
17.
【答案】
【解答】
解:∵
,,
∴
,
∴
,
∵
,
∴
,
∴
,
∴
,
故答案为:.
18.
【答案】
【解答】
解:设这种商品每件的进价为元,
则:,
解得:.
故答案为:.
19.
【答案】
,
【解答】
解:的平方根是;
,,
∵
,
∴
.
故答案为:;.
20.
【答案】
,垂线段最短
【解答】
根据点到直线的距离的定义得出线段的长是点到直线的距离,从直线外一点到这条直线所作的垂线段最短.
三、
解答题
(本题共计
7
小题
,每题
10
分
,共计70分
)
21.
【答案】
原式=
=.
【解答】
原式=
=.
22.
【答案】
解:左图:与是与被直线所截形成的内错角,
与是直线与直线被直线所截形成的内错角;
右图:与是与被直线所截形成的同旁内角,
与是直线与直线被直线所截形成的同位角.
【解答】
解:左图:与是与被直线所截形成的内错角,
与是直线与直线被直线所截形成的内错角;
右图:与是与被直线所截形成的同旁内角,
与是直线与直线被直线所截形成的同位角.
23.
【答案】
解:设正方形与轴的交点分别为,(点在点下方),
与轴交于、点(点在点右方),如图所示:
∵
正方形的边长为,且中心为坐标原点,
∴
,
∴
点的坐标为,点的坐标为,点的坐标为,点的坐标为.
,点的横(纵)坐标互为相反数.
连接,,如图所示:
∵
坐标原点为正方形的中心,且正方形的对角线互相平分,
∴
点为线段的中点,
∴
,点的横(纵)坐标互为相反数.
【解答】
解:设正方形与轴的交点分别为,(点在点下方),
与轴交于、点(点在点右方),如图所示:
∵
正方形的边长为,且中心为坐标原点,
∴
,
∴
点的坐标为,点的坐标为,点的坐标为,点的坐标为.
,点的横(纵)坐标互为相反数.
连接,,如图所示:
∵
坐标原点为正方形的中心,且正方形的对角线互相平分,
∴
点为线段的中点,
∴
,点的横(纵)坐标互为相反数.
24.
【答案】
∵
=,=,
∴
=,
又∵
,
∴
=,=
∴
=,
又∵
平分,
∴
=,
∴
=;
若=时,
同理可得:
=;
=
【解答】
∵
=,=,
∴
=,
又∵
,
∴
=,=
∴
=,
又∵
平分,
∴
=,
∴
=;
若=时,
同理可得:
=;
=
25.
【答案】
解:建立平面直角坐标系如图所示,
,,,,,.
【解答】
解:建立平面直角坐标系如图所示,
,,,,,.
26.
【答案】
,
去分母得:,
解得:;
,
去分母得:,
解得:.
【解答】
解:根据方程的定义,若选择其中两个整式用等号连接,则共能组成个方程.
故答案为:.
(2),
去分母得:,
解得:;
,
去分母得:,
解得:.
27.
【答案】
解:如图,∵
与轴的夹角为,四边形为正方形,
∴
,
∴
,
,
∵
点在第二象限,
∴
点的坐标为;
∵
与轴的夹角为,
∴
,
∴
,
,
∴
,
在中,,
∴
,
,
∴
,
∵
点在第二象限,
∴
点的坐标为.
【解答】
解:如图,∵
与轴的夹角为,四边形为正方形,
∴
,
∴
,
,
∵
点在第二象限,
∴
点的坐标为;
∵
与轴的夹角为,
∴
,
∴
,
,
∴
,
在中,,
∴
,
,
∴
,
∵
点在第二象限,
∴
点的坐标为.
.
同课章节目录
