人教版数学九年级上册 第24章 24.1圆的有关性质同步测试试题(一)(Word版 含解析)
文档属性
| 名称 | 人教版数学九年级上册 第24章 24.1圆的有关性质同步测试试题(一)(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 290.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-17 20:43:45 | ||
图片预览



文档简介
圆的有关性质同步测试试题(一)
一.选择题
1.如图,四边形ABCD的四个顶点均在半圆O上,若∠A=50°,则∠C=( )
A.130°
B.120°
C.125°
D.110°
2.如图,⊙O的弦AB垂直平分半径OC,若⊙O的半径为2,则弦AB的长为( )
A.
B.
C.
D.
3.如图,A、B、C三点在⊙O上,若∠ACB=∠AOB,则∠AOB的度数是( )
A.60°
B.90°
C.100°
D.120°
4.如图AB为⊙O的直径,∠BED=40°,则∠ACD=( )
A.40°
B.45
C.50°
D.55°
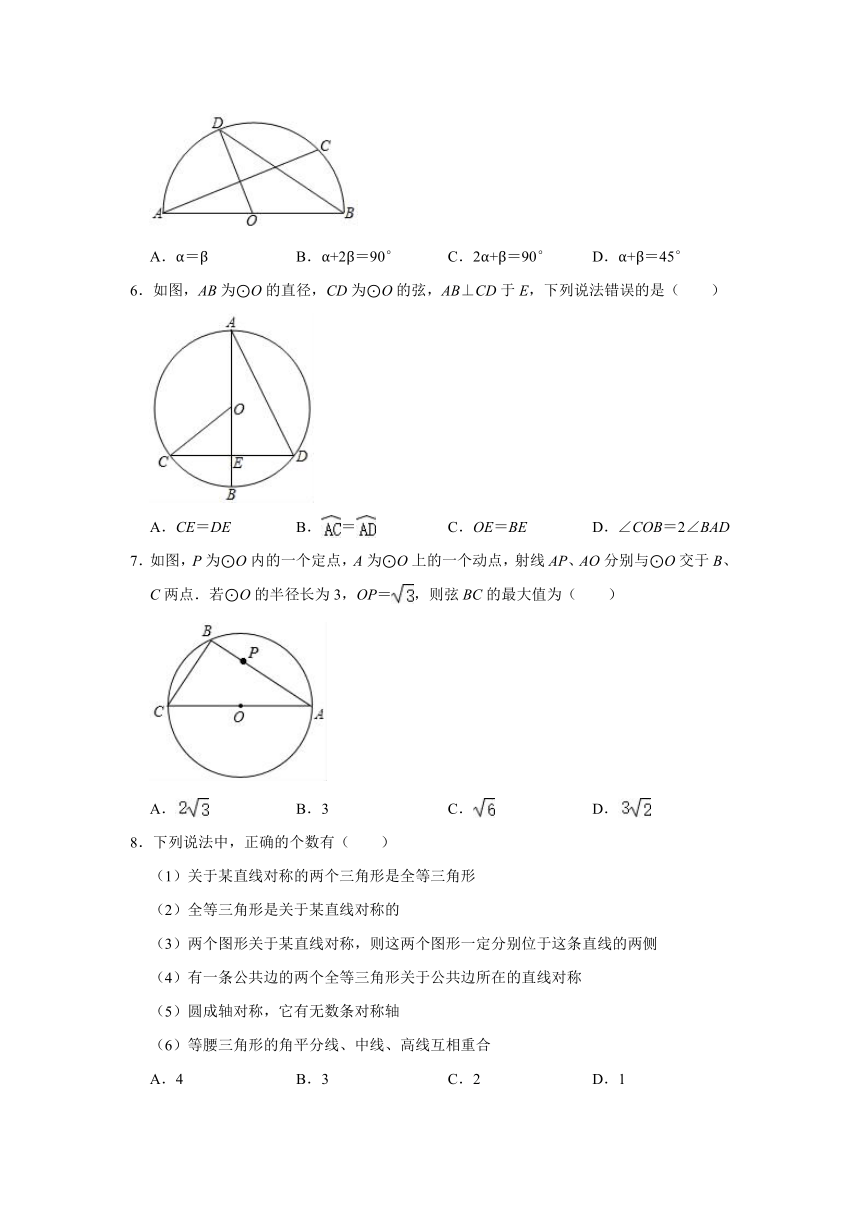
5.如图,AB是圆O的直径,点C是半圆O上不同于A,B的一点,点D为弧AC的中点,连结OD,BD,AC,设∠CAB=β,∠BDO=α,则( )
A.α=β
B.α+2β=90°
C.2α+β=90°
D.α+β=45°
6.如图,AB为⊙O的直径,CD为⊙O的弦,AB⊥CD于E,下列说法错误的是( )
A.CE=DE
B.=
C.OE=BE
D.∠COB=2∠BAD
7.如图,P为⊙O内的一个定点,A为⊙O上的一个动点,射线AP、AO分别与⊙O交于B、C两点.若⊙O的半径长为3,OP=,则弦BC的最大值为( )
A.
B.3
C.
D.
8.下列说法中,正确的个数有( )
(1)关于某直线对称的两个三角形是全等三角形
(2)全等三角形是关于某直线对称的
(3)两个图形关于某直线对称,则这两个图形一定分别位于这条直线的两侧
(4)有一条公共边的两个全等三角形关于公共边所在的直线对称
(5)圆成轴对称,它有无数条对称轴
(6)等腰三角形的角平分线、中线、高线互相重合
A.4
B.3
C.2
D.1
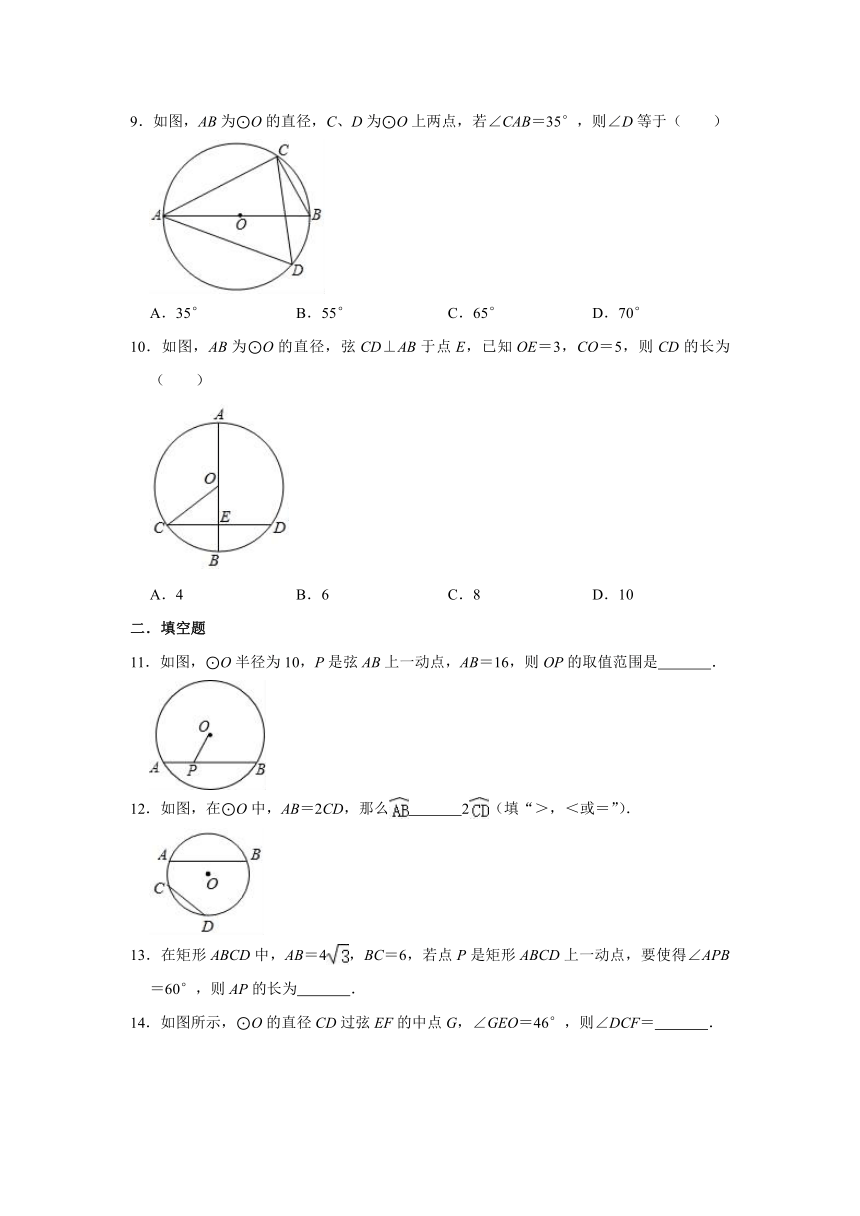
9.如图,AB为⊙O的直径,C、D为⊙O上两点,若∠CAB=35°,则∠D等于( )
A.35°
B.55°
C.65°
D.70°
10.如图,AB为⊙O的直径,弦CD⊥AB于点E,已知OE=3,CO=5,则CD的长为( )
A.4
B.6
C.8
D.10
二.填空题
11.如图,⊙O半径为10,P是弦AB上一动点,AB=16,则OP的取值范围是
.
12.如图,在⊙O中,AB=2CD,那么
2(填“>,<或=”).
13.在矩形ABCD中,AB=4,BC=6,若点P是矩形ABCD上一动点,要使得∠APB=60°,则AP的长为
.
14.如图所示,⊙O的直径CD过弦EF的中点G,∠GEO=46°,则∠DCF=
.
15.如图,一块含30°角的直角三角板,将它的30°角顶点A落在⊙O上,边AB、AC分别与⊙O交于点D、E,则∠DOE的度数为
.
三.解答题
16.如图,已知四边形ABCD内接于⊙O,AC⊥BD于E,=.
(1)求证:∠BDC=2∠ADB;
(2)若直径BM交AC于点N,AD﹣BN=2,BC=8,求⊙O的半径.
17.《九章算术》是我国古代著名数学经典,其中对勾股定理的论述比西方早一千多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小:以锯锯之,深一寸,锯道长一尺.问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深1寸,锯道长1尺.如图,已知弦AB=1尺,弓形高CD=1寸,(注:1尺=10寸)问这块圆柱形木材的直径是多少寸?
18.如图,在⊙O中,AB是⊙O的直径,点C在⊙O上,OD⊥AC于点D,延长DO交⊙O于点E,连接EC、EB、BC,若AC=6,OD=.
(1)求⊙O的直径;
(2)求△BEC的面积.
19.如图,AB是⊙O的直径,∠ACD=20°,求∠BAD的度数.
参考答案与试题解析
一.选择题
1.【解答】解:∵四边形ABCD的四个顶点均在半圆O上,
∴∠A+∠C=180°,
∵∠A=50°,
∴∠C=180°﹣50°=130°.
故选:A.
2.【解答】解:连接OA,如图:
∵弦AB垂直平分半径OC,OC=2,
∴OE=OC=1,AE=BE,
在Rt△AOE中,由勾股定理得:AE===,
∴AB=2AE=2,
故选:D.
3.【解答】解:如图,在优弧AB上取一点D,连接AD,BD.
∵∠ACB+∠ADB=180°,∠ACB=∠AOB=2∠ADB,
∴2∠ADB+∠ADB=180°,
∴∠ADB=60°,
∴∠AOB=2∠ADB=120°,
故选:D.
4.【解答】解:连接OD,如图,
∵∠BOD=2∠BED=2×40°=80°,
∴∠AOD=180°﹣∠BOD=180°﹣80°=100°,
∴∠ACD=∠AOD=×100°=50°.
故选:C.
5.【解答】解:如图,设AC与DO交点为E,如图,
∵OD=OB,
∴∠OBD=∠BDO=α,
∴∠DOA=2∠OBD=2α,
又∵D为中点,AB为⊙O直径,
∴OD⊥AC,
∴∠EAO+∠EOA=90°,
即2α+β=90°.
故选:C.
6.【解答】解:连接OD,如图,
∵AB⊥CD,
∴CE=DE,=,=,
∵=,
∴∠BOC=∠BOD,
∵∠BOD=2∠BAD,
∴∠BOC=2∠BAD.
故选:C.
7.【解答】解:过点O作OE⊥AB于E,如图:
∵O为圆心,
∴AE=BE,
∴OE=BC,
∵OE≤OP,
∴BC≤2OP,
∴当E、P重合时,即OP垂直AB时,BC取最大值,
∴弦BC的最大值为:2OP=2.
故选:A.
8.【解答】解:(1)关于某直线对称的两个三角形是全等三角形,正确,符合题意;
(2)全等三角形是关于某直线对称的,错误,不符合题意;
(3)两个图形关于某直线对称,则这两个图形一定分别位于这条直线的两侧,错误,不符合题意;
(4)有一条公共边的两个全等三角形关于公共边所在的直线对称,错误,不符合题意;
(5)圆成轴对称,它有无数条对称轴,正确,符合题意;
(6)等腰三角形的顶角平分线、底边的中线、底边的高线互相重合,故错误,不符合题意,
正确的有2个,
故选:C.
9.【解答】解:∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠B=90°﹣∠CAB=90°﹣35°=55°,
∴∠D=∠B=55°.
故选:B.
10.【解答】解:∵AB为⊙O的直径,弦CD⊥AB,
∴DE=CE===4,
∴CD=2CE=8,
故选:C.
二.填空题(共5小题)
11.【解答】解:过点O作OC⊥AB于C.
∴AC=AB==8,
∵⊙O的半径OA=10,
∴在Rt△OAC中,OC==6,
∴当P与A或B重合时,OP最长为10,
当P与C重合时,OP最短为6,
∴线段OP长度的取值范围是:6≤OP≤10.
故答案为:6≤OP≤10.
12.【解答】解:如图,过点O作OM⊥AB,垂足为N,交⊙O于点M,连接MA,MB,
由垂径定理得,AN=BN,=,
∵AB=2CD,
∵AN=BN=CD,
又∵MA>AN,
∴MA>CD,
∴>,
∴2>2,
即,>2,
故答案为:>.
13.【解答】解:如图,取CD中点P,连接AP,BP,
∵四边形ABCD是矩形,
∴AB=CD=4,AD=BC=6,∠D=∠C=90°,
∵点P是CD中点,
∴CP=DP=2,
∴AP===4,
BP===4,
∴AP=PB=AB,
∴△APB是等边三角形,
∴∠APB=60°,
过点A,点P,点B作圆与AD交于点P′,与BC交于点P″,连接BP′,AP″,
此时∠AP′B=∠APB=60°,∠AP″B=60°,
∴AP′==4,AP″==8,
故答案为:4或4或8.
14.【解答】解:∵CD是直径,EG=GF,
∴CD⊥EF,
∴=,
∴∠CDF=∠EOD,
∵∠OGE=90°,∠GEO=46°,
∴∠EOD=44°,
∴∠DCF=22°.
故答案为:22°.
15.【解答】解:∵∠BAC=30°,
∴∠EOD=2∠BAC=60°,
故答案为:60°.
三.解答题(共4小题)
16.【解答】(1)证明:如图1,作直径DG,交AC于F,交BC于P,交⊙O于G,连接CG,
∵=.
∴DG⊥BC,BD=CD,
∴∠CBD=∠BCD,
∵AC⊥BD,
∴∠DEF=90°,
∵∠CPF=90°,
∴∠DEF=∠CPF,
∵∠DFE=∠CFP,
∴∠EDF=∠ACB=∠ADB=∠CDG,
∴∠BDC=2∠ADB;
(2)解:如图2,作直径DG,交AC于F,交BC于P,交⊙O于G,连接CG,BG,
由(1)知:∠ADB=∠BDG=∠CDG,
∴=,
∴∠CBG=∠BCA,
∴BG∥AC,
∴∠ONF=∠OBG,∠OFN=∠OGB,
∵OB=OG,
∴∠OBG=∠OGB,
∴∠ONF=∠OFN,
∴OF=ON,
∵AC⊥BD,∠ADB=∠FDB,
∴∠DAE=∠AFD,
∴AB=DF,
同理得:CF=CG,
∴AD﹣BN,
=DF﹣BN
=OD+OF﹣(OB﹣ON)
=OF+ON=2,
∴OF=ON=1,
∵CF=CG,CP⊥FG,
∴FP=PG,
设FP=a,则OB=OG=2a+1,FP=a+1,
∵DG⊥BC,且BC=8,
∴BP=BC=4,
Rt△OBP中,OB2=OP2+BP2,
∴(2a+1)2=(a+1)2+42,
3a2+2a﹣16=0,
(a﹣2)(3a+8)=0,
∴a1=2,a2=﹣(舍),
∴⊙O的半径OG=2a+1=5.
17.【解答】解:设⊙O的半径为r.
∵OC⊥AB,
∴AD=BD=AB=5,
在Rt△ADO中,AD=5,OD=r﹣1,OA=r,
则有:r2=52+(r﹣1)2,
解得:r=13,
∴⊙O的直径为26寸.
18.【解答】解:(1)∵OD⊥AC,AC=6,
∴AD=3,
∵OD=,
∴OA=4,
∴⊙O的直径=8;
(2)过点E作EF⊥CB,交CB的延长线于点F,
∵AB为直径,
∴∠ACB=∠CDE=∠CFE=90°,
∴四边形CDEF为矩形,
∴EF=CD=AC=3,BC===2,
∴S△BEC=×BC×EF=×3=3.
19.【解答】解:∵,
∴∠ABD=∠ACD=20°,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠BAD=180°﹣∠ADB﹣∠ABD=180°﹣90°﹣20°=70°.
一.选择题
1.如图,四边形ABCD的四个顶点均在半圆O上,若∠A=50°,则∠C=( )
A.130°
B.120°
C.125°
D.110°
2.如图,⊙O的弦AB垂直平分半径OC,若⊙O的半径为2,则弦AB的长为( )
A.
B.
C.
D.
3.如图,A、B、C三点在⊙O上,若∠ACB=∠AOB,则∠AOB的度数是( )
A.60°
B.90°
C.100°
D.120°
4.如图AB为⊙O的直径,∠BED=40°,则∠ACD=( )
A.40°
B.45
C.50°
D.55°
5.如图,AB是圆O的直径,点C是半圆O上不同于A,B的一点,点D为弧AC的中点,连结OD,BD,AC,设∠CAB=β,∠BDO=α,则( )
A.α=β
B.α+2β=90°
C.2α+β=90°
D.α+β=45°
6.如图,AB为⊙O的直径,CD为⊙O的弦,AB⊥CD于E,下列说法错误的是( )
A.CE=DE
B.=
C.OE=BE
D.∠COB=2∠BAD
7.如图,P为⊙O内的一个定点,A为⊙O上的一个动点,射线AP、AO分别与⊙O交于B、C两点.若⊙O的半径长为3,OP=,则弦BC的最大值为( )
A.
B.3
C.
D.
8.下列说法中,正确的个数有( )
(1)关于某直线对称的两个三角形是全等三角形
(2)全等三角形是关于某直线对称的
(3)两个图形关于某直线对称,则这两个图形一定分别位于这条直线的两侧
(4)有一条公共边的两个全等三角形关于公共边所在的直线对称
(5)圆成轴对称,它有无数条对称轴
(6)等腰三角形的角平分线、中线、高线互相重合
A.4
B.3
C.2
D.1
9.如图,AB为⊙O的直径,C、D为⊙O上两点,若∠CAB=35°,则∠D等于( )
A.35°
B.55°
C.65°
D.70°
10.如图,AB为⊙O的直径,弦CD⊥AB于点E,已知OE=3,CO=5,则CD的长为( )
A.4
B.6
C.8
D.10
二.填空题
11.如图,⊙O半径为10,P是弦AB上一动点,AB=16,则OP的取值范围是
.
12.如图,在⊙O中,AB=2CD,那么
2(填“>,<或=”).
13.在矩形ABCD中,AB=4,BC=6,若点P是矩形ABCD上一动点,要使得∠APB=60°,则AP的长为
.
14.如图所示,⊙O的直径CD过弦EF的中点G,∠GEO=46°,则∠DCF=
.
15.如图,一块含30°角的直角三角板,将它的30°角顶点A落在⊙O上,边AB、AC分别与⊙O交于点D、E,则∠DOE的度数为
.
三.解答题
16.如图,已知四边形ABCD内接于⊙O,AC⊥BD于E,=.
(1)求证:∠BDC=2∠ADB;
(2)若直径BM交AC于点N,AD﹣BN=2,BC=8,求⊙O的半径.
17.《九章算术》是我国古代著名数学经典,其中对勾股定理的论述比西方早一千多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小:以锯锯之,深一寸,锯道长一尺.问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深1寸,锯道长1尺.如图,已知弦AB=1尺,弓形高CD=1寸,(注:1尺=10寸)问这块圆柱形木材的直径是多少寸?
18.如图,在⊙O中,AB是⊙O的直径,点C在⊙O上,OD⊥AC于点D,延长DO交⊙O于点E,连接EC、EB、BC,若AC=6,OD=.
(1)求⊙O的直径;
(2)求△BEC的面积.
19.如图,AB是⊙O的直径,∠ACD=20°,求∠BAD的度数.
参考答案与试题解析
一.选择题
1.【解答】解:∵四边形ABCD的四个顶点均在半圆O上,
∴∠A+∠C=180°,
∵∠A=50°,
∴∠C=180°﹣50°=130°.
故选:A.
2.【解答】解:连接OA,如图:
∵弦AB垂直平分半径OC,OC=2,
∴OE=OC=1,AE=BE,
在Rt△AOE中,由勾股定理得:AE===,
∴AB=2AE=2,
故选:D.
3.【解答】解:如图,在优弧AB上取一点D,连接AD,BD.
∵∠ACB+∠ADB=180°,∠ACB=∠AOB=2∠ADB,
∴2∠ADB+∠ADB=180°,
∴∠ADB=60°,
∴∠AOB=2∠ADB=120°,
故选:D.
4.【解答】解:连接OD,如图,
∵∠BOD=2∠BED=2×40°=80°,
∴∠AOD=180°﹣∠BOD=180°﹣80°=100°,
∴∠ACD=∠AOD=×100°=50°.
故选:C.
5.【解答】解:如图,设AC与DO交点为E,如图,
∵OD=OB,
∴∠OBD=∠BDO=α,
∴∠DOA=2∠OBD=2α,
又∵D为中点,AB为⊙O直径,
∴OD⊥AC,
∴∠EAO+∠EOA=90°,
即2α+β=90°.
故选:C.
6.【解答】解:连接OD,如图,
∵AB⊥CD,
∴CE=DE,=,=,
∵=,
∴∠BOC=∠BOD,
∵∠BOD=2∠BAD,
∴∠BOC=2∠BAD.
故选:C.
7.【解答】解:过点O作OE⊥AB于E,如图:
∵O为圆心,
∴AE=BE,
∴OE=BC,
∵OE≤OP,
∴BC≤2OP,
∴当E、P重合时,即OP垂直AB时,BC取最大值,
∴弦BC的最大值为:2OP=2.
故选:A.
8.【解答】解:(1)关于某直线对称的两个三角形是全等三角形,正确,符合题意;
(2)全等三角形是关于某直线对称的,错误,不符合题意;
(3)两个图形关于某直线对称,则这两个图形一定分别位于这条直线的两侧,错误,不符合题意;
(4)有一条公共边的两个全等三角形关于公共边所在的直线对称,错误,不符合题意;
(5)圆成轴对称,它有无数条对称轴,正确,符合题意;
(6)等腰三角形的顶角平分线、底边的中线、底边的高线互相重合,故错误,不符合题意,
正确的有2个,
故选:C.
9.【解答】解:∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠B=90°﹣∠CAB=90°﹣35°=55°,
∴∠D=∠B=55°.
故选:B.
10.【解答】解:∵AB为⊙O的直径,弦CD⊥AB,
∴DE=CE===4,
∴CD=2CE=8,
故选:C.
二.填空题(共5小题)
11.【解答】解:过点O作OC⊥AB于C.
∴AC=AB==8,
∵⊙O的半径OA=10,
∴在Rt△OAC中,OC==6,
∴当P与A或B重合时,OP最长为10,
当P与C重合时,OP最短为6,
∴线段OP长度的取值范围是:6≤OP≤10.
故答案为:6≤OP≤10.
12.【解答】解:如图,过点O作OM⊥AB,垂足为N,交⊙O于点M,连接MA,MB,
由垂径定理得,AN=BN,=,
∵AB=2CD,
∵AN=BN=CD,
又∵MA>AN,
∴MA>CD,
∴>,
∴2>2,
即,>2,
故答案为:>.
13.【解答】解:如图,取CD中点P,连接AP,BP,
∵四边形ABCD是矩形,
∴AB=CD=4,AD=BC=6,∠D=∠C=90°,
∵点P是CD中点,
∴CP=DP=2,
∴AP===4,
BP===4,
∴AP=PB=AB,
∴△APB是等边三角形,
∴∠APB=60°,
过点A,点P,点B作圆与AD交于点P′,与BC交于点P″,连接BP′,AP″,
此时∠AP′B=∠APB=60°,∠AP″B=60°,
∴AP′==4,AP″==8,
故答案为:4或4或8.
14.【解答】解:∵CD是直径,EG=GF,
∴CD⊥EF,
∴=,
∴∠CDF=∠EOD,
∵∠OGE=90°,∠GEO=46°,
∴∠EOD=44°,
∴∠DCF=22°.
故答案为:22°.
15.【解答】解:∵∠BAC=30°,
∴∠EOD=2∠BAC=60°,
故答案为:60°.
三.解答题(共4小题)
16.【解答】(1)证明:如图1,作直径DG,交AC于F,交BC于P,交⊙O于G,连接CG,
∵=.
∴DG⊥BC,BD=CD,
∴∠CBD=∠BCD,
∵AC⊥BD,
∴∠DEF=90°,
∵∠CPF=90°,
∴∠DEF=∠CPF,
∵∠DFE=∠CFP,
∴∠EDF=∠ACB=∠ADB=∠CDG,
∴∠BDC=2∠ADB;
(2)解:如图2,作直径DG,交AC于F,交BC于P,交⊙O于G,连接CG,BG,
由(1)知:∠ADB=∠BDG=∠CDG,
∴=,
∴∠CBG=∠BCA,
∴BG∥AC,
∴∠ONF=∠OBG,∠OFN=∠OGB,
∵OB=OG,
∴∠OBG=∠OGB,
∴∠ONF=∠OFN,
∴OF=ON,
∵AC⊥BD,∠ADB=∠FDB,
∴∠DAE=∠AFD,
∴AB=DF,
同理得:CF=CG,
∴AD﹣BN,
=DF﹣BN
=OD+OF﹣(OB﹣ON)
=OF+ON=2,
∴OF=ON=1,
∵CF=CG,CP⊥FG,
∴FP=PG,
设FP=a,则OB=OG=2a+1,FP=a+1,
∵DG⊥BC,且BC=8,
∴BP=BC=4,
Rt△OBP中,OB2=OP2+BP2,
∴(2a+1)2=(a+1)2+42,
3a2+2a﹣16=0,
(a﹣2)(3a+8)=0,
∴a1=2,a2=﹣(舍),
∴⊙O的半径OG=2a+1=5.
17.【解答】解:设⊙O的半径为r.
∵OC⊥AB,
∴AD=BD=AB=5,
在Rt△ADO中,AD=5,OD=r﹣1,OA=r,
则有:r2=52+(r﹣1)2,
解得:r=13,
∴⊙O的直径为26寸.
18.【解答】解:(1)∵OD⊥AC,AC=6,
∴AD=3,
∵OD=,
∴OA=4,
∴⊙O的直径=8;
(2)过点E作EF⊥CB,交CB的延长线于点F,
∵AB为直径,
∴∠ACB=∠CDE=∠CFE=90°,
∴四边形CDEF为矩形,
∴EF=CD=AC=3,BC===2,
∴S△BEC=×BC×EF=×3=3.
19.【解答】解:∵,
∴∠ABD=∠ACD=20°,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠BAD=180°﹣∠ADB﹣∠ABD=180°﹣90°﹣20°=70°.
同课章节目录
