抛物线及其标准方程教案
图片预览
文档简介
抛物线及其标准方程
学 科 数 学 授课班级
授课人 日 期
教学目标 知识与技能 掌握抛物线的定义、几何图形,明确焦点和准线的意义会推导抛物线的标准方程能够利用给定的条件求抛物线的标准方程
过程与方法 通过“观察”“思考”“探究”与“合作交流”等一系列数学活动,培养学生观察、类比、分析、概括的能力以及逻辑思维的能力,能使学生学会数学思考与推理,学会反思与感悟,形成良好的数学观,并进一步感受坐标法及数形结合的思想
情感、态度与价值观 通过提问、讨论、思考解答等教学活动,进一步培养学生合作、交流的能力和团队精神,培养学生善于观察、勇于探索、严密细致的科学态度;激发学生积极主动地参与数学学习活动,养成良好的学习习惯。
重点 抛物线的定义及其标准方程
难点 抛物线定义的形成过程及抛物线标准方程的推导(关键是坐标系方案的选择)
教学过程 教学方法和设计意图
创设情境 类比联想,提出课题师:前面我们一起研究了椭圆、双曲线的定义,标准方程,几何性质,大家想一想:椭圆、双曲线的共同特点是什么? 生:与一个 定点的距离和一条定直线的距离的比是常数e的点的轨迹,当0<e<1时是椭圆,当e>1时是双曲线,那么,当e=1时,它是什么曲线呢? 迁移引导,设置悬念
探索研究一、概念探究二、标准方程的探究 实验、演示,观察猜想1、几何画板课件演示:学生观察 ① 动点M到焦点F的距离|MF|与动点M到定直线l的距离d之间的关系;② 观察追踪动点M得到的轨迹形状。
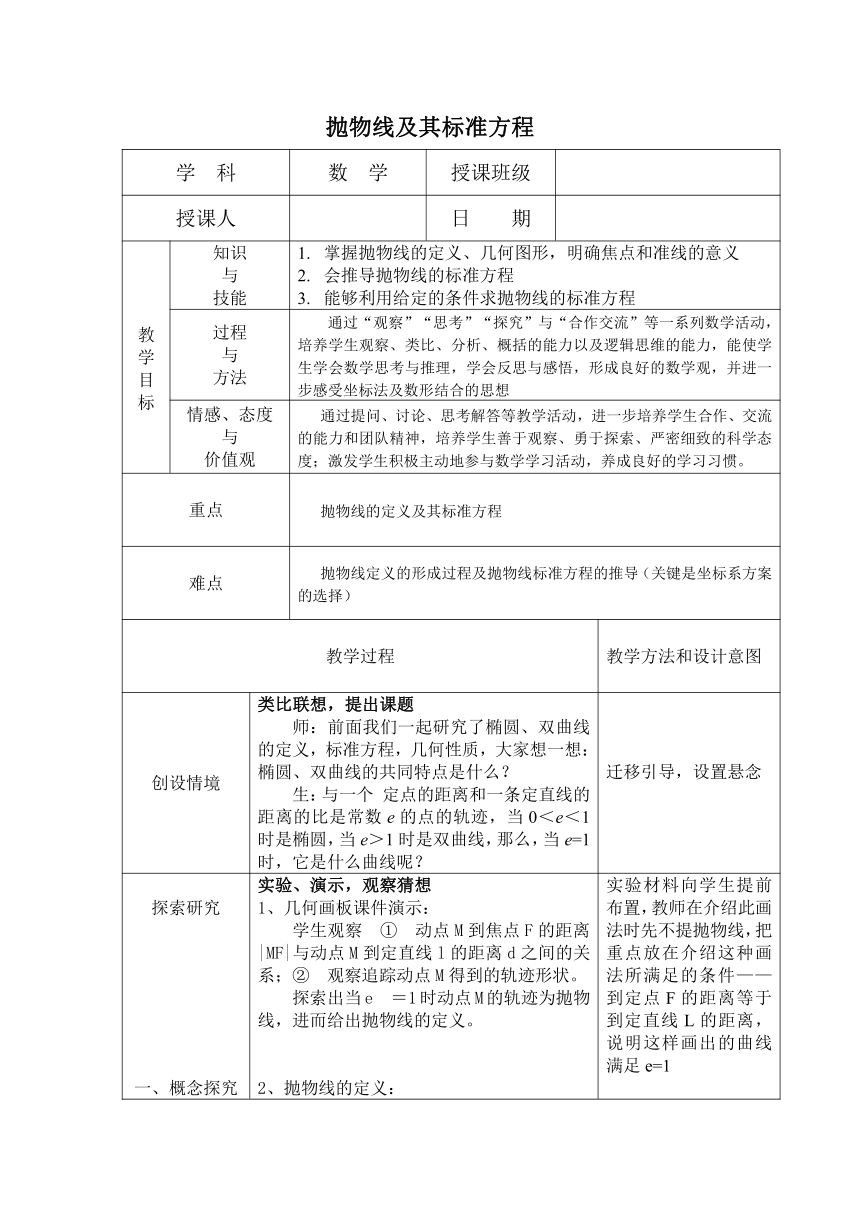
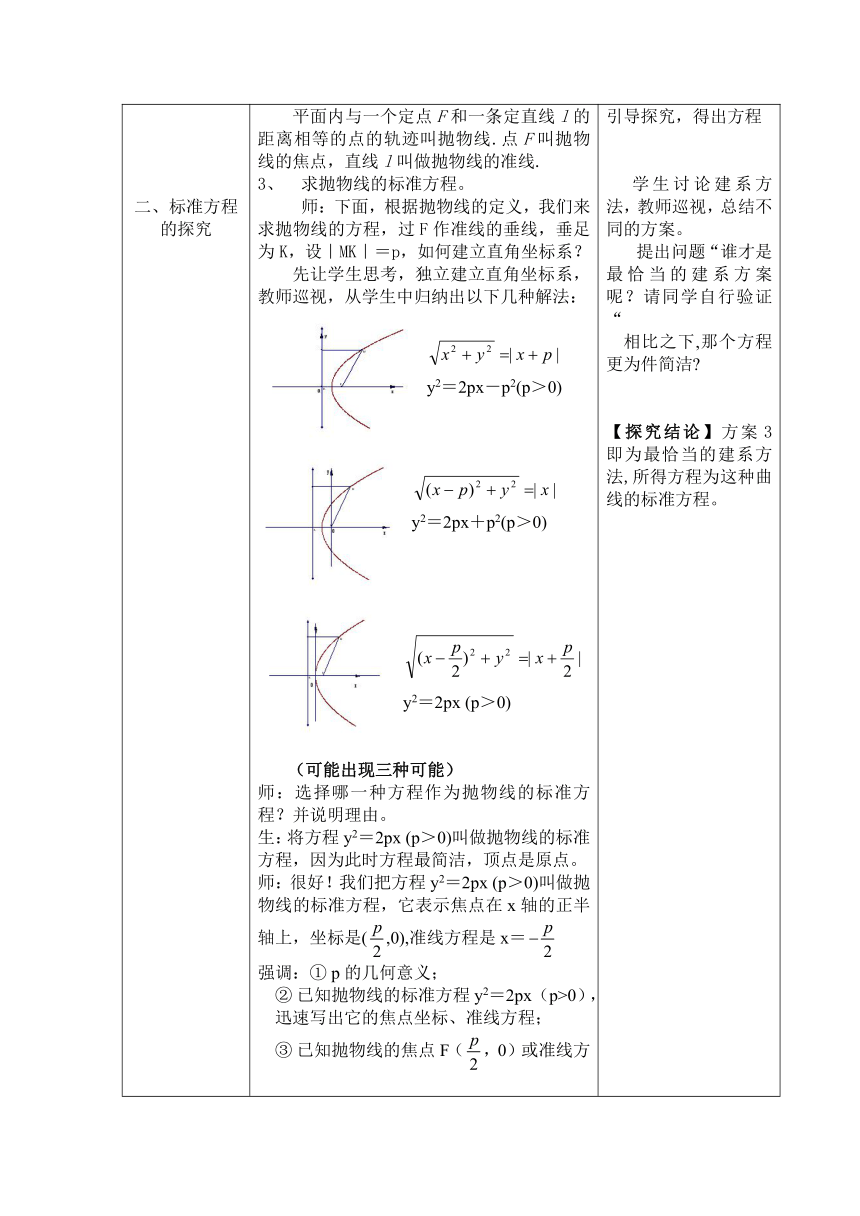
探索出当e =1时动点M的轨迹为抛物线,进而给出抛物线的定义。2、抛物线的定义:平面内与一个定点F和一条定直线l的距离相等的点的轨迹叫抛物线.点F叫抛物线的焦点,直线l叫做抛物线的准线.3、 求抛物线的标准方程。师:下面,根据抛物线的定义,我们来求抛物线的方程,过F作准线的垂线,垂足为K,设|MK|=p,如何建立直角坐标系?先让学生思考,独立建立直角坐标系,教师巡视,从学生中归纳出以下几种解法: y2=2px-p2(p>0)y2=2px+p2(p>0)y2=2px (p>0)(可能出现三种可能)师:选择哪一种方程作为抛物线的标准方程?并说明理由。生:将方程y2=2px (p>0)叫做抛物线的标准方程,因为此时方程最简洁,顶点是原点。师:很好!我们把方程y2=2px (p>0)叫做抛物线的标准方程,它表示焦点在x轴的正半轴上,坐标是(,0),准线方程是x=强调:① p的几何意义;
② 已知抛物线的标准方程y2=2px (p>0),迅速写出它的焦点坐标、准线方程;
③ 已知抛物线的焦点F(,0)或准线方程x=(p>0),迅速写出其标准方程。4、讨论四种位置上的抛物线标准方程
利用几何画板,展示准线与焦点的四个不同的位置关系,由学生说出标准方程,焦点坐标及准线方程【注意】图形的位置特征和方程的形式应结合起来记忆,通过四种标准方程对比,总结出①方程的一次项决定焦点的位置。②一次项系数的符号决定开口方向。 实验材料向学生提前布置,教师在介绍此画法时先不提抛物线,把重点放在介绍这种画法所满足的条件——到定点F的距离等于到定直线L的距离,说明这样画出的曲线满足e=1
引导探究,得出方程学生讨论建系方法,教师巡视,总结不同的方案。提出问题“谁才是最恰当的建系方案呢?请同学自行验证“ 相比之下,那个方程更为件简洁 【探究结论】方案3即为最恰当的建系方法,所得方程为这种曲线的标准方程。总结四种形式抛物线标准方程,使本节的知识系统化
例题讲解 实践探索,形成能力例1 (1)已知抛物线的标准方程是,求它的焦点坐标和准线方程;已知抛物线的焦点是,求它的标准方程.(3)已知抛物线的准线方程是y=3,求它的标准方程. 巩固四种方程的形式及曲线特征,熟悉相关公式。注意图形在解题过程中的作用,渗透数形结合的思想。
课堂练习 练习巩固,加深理解根据下列条件写出抛物线的标准方程:⑴焦点坐标是(0,4);⑵准线方程是x=2;⑶焦点到准线的距离是8 师生共同评改
能力提升内容拓展 1.根据下列条件写出抛物线的标准方程(1)焦点是F(3,0);(2)准线方程是x=1/4;(3)焦点到准线的距离是2;2.求下列抛物线的焦点坐标与准线方程(1)y2=28x; (2)4x2=y; (3)2y2+x=0;已知抛物线经过点(-4,-2),求它的标准方程 此题对学生思维水平要求较高,针对学生素质的差异,使学有余力的同学有所提高,从而达到“拔尖”的目的
课堂小结 教学内容1,抛物线的定义2,抛物线的标准方程3,标准方程的应用数学思想:数形结合思想分类讨论的思想解题方法:待定系数法
本课作业
板书设计
标准方程 图形 焦点 准线
EMBED Equation.DSMT4
EMBED Equation.DSMT4
学 科 数 学 授课班级
授课人 日 期
教学目标 知识与技能 掌握抛物线的定义、几何图形,明确焦点和准线的意义会推导抛物线的标准方程能够利用给定的条件求抛物线的标准方程
过程与方法 通过“观察”“思考”“探究”与“合作交流”等一系列数学活动,培养学生观察、类比、分析、概括的能力以及逻辑思维的能力,能使学生学会数学思考与推理,学会反思与感悟,形成良好的数学观,并进一步感受坐标法及数形结合的思想
情感、态度与价值观 通过提问、讨论、思考解答等教学活动,进一步培养学生合作、交流的能力和团队精神,培养学生善于观察、勇于探索、严密细致的科学态度;激发学生积极主动地参与数学学习活动,养成良好的学习习惯。
重点 抛物线的定义及其标准方程
难点 抛物线定义的形成过程及抛物线标准方程的推导(关键是坐标系方案的选择)
教学过程 教学方法和设计意图
创设情境 类比联想,提出课题师:前面我们一起研究了椭圆、双曲线的定义,标准方程,几何性质,大家想一想:椭圆、双曲线的共同特点是什么? 生:与一个 定点的距离和一条定直线的距离的比是常数e的点的轨迹,当0<e<1时是椭圆,当e>1时是双曲线,那么,当e=1时,它是什么曲线呢? 迁移引导,设置悬念
探索研究一、概念探究二、标准方程的探究 实验、演示,观察猜想1、几何画板课件演示:学生观察 ① 动点M到焦点F的距离|MF|与动点M到定直线l的距离d之间的关系;② 观察追踪动点M得到的轨迹形状。
探索出当e =1时动点M的轨迹为抛物线,进而给出抛物线的定义。2、抛物线的定义:平面内与一个定点F和一条定直线l的距离相等的点的轨迹叫抛物线.点F叫抛物线的焦点,直线l叫做抛物线的准线.3、 求抛物线的标准方程。师:下面,根据抛物线的定义,我们来求抛物线的方程,过F作准线的垂线,垂足为K,设|MK|=p,如何建立直角坐标系?先让学生思考,独立建立直角坐标系,教师巡视,从学生中归纳出以下几种解法: y2=2px-p2(p>0)y2=2px+p2(p>0)y2=2px (p>0)(可能出现三种可能)师:选择哪一种方程作为抛物线的标准方程?并说明理由。生:将方程y2=2px (p>0)叫做抛物线的标准方程,因为此时方程最简洁,顶点是原点。师:很好!我们把方程y2=2px (p>0)叫做抛物线的标准方程,它表示焦点在x轴的正半轴上,坐标是(,0),准线方程是x=强调:① p的几何意义;
② 已知抛物线的标准方程y2=2px (p>0),迅速写出它的焦点坐标、准线方程;
③ 已知抛物线的焦点F(,0)或准线方程x=(p>0),迅速写出其标准方程。4、讨论四种位置上的抛物线标准方程
利用几何画板,展示准线与焦点的四个不同的位置关系,由学生说出标准方程,焦点坐标及准线方程【注意】图形的位置特征和方程的形式应结合起来记忆,通过四种标准方程对比,总结出①方程的一次项决定焦点的位置。②一次项系数的符号决定开口方向。 实验材料向学生提前布置,教师在介绍此画法时先不提抛物线,把重点放在介绍这种画法所满足的条件——到定点F的距离等于到定直线L的距离,说明这样画出的曲线满足e=1
引导探究,得出方程学生讨论建系方法,教师巡视,总结不同的方案。提出问题“谁才是最恰当的建系方案呢?请同学自行验证“ 相比之下,那个方程更为件简洁 【探究结论】方案3即为最恰当的建系方法,所得方程为这种曲线的标准方程。总结四种形式抛物线标准方程,使本节的知识系统化
例题讲解 实践探索,形成能力例1 (1)已知抛物线的标准方程是,求它的焦点坐标和准线方程;已知抛物线的焦点是,求它的标准方程.(3)已知抛物线的准线方程是y=3,求它的标准方程. 巩固四种方程的形式及曲线特征,熟悉相关公式。注意图形在解题过程中的作用,渗透数形结合的思想。
课堂练习 练习巩固,加深理解根据下列条件写出抛物线的标准方程:⑴焦点坐标是(0,4);⑵准线方程是x=2;⑶焦点到准线的距离是8 师生共同评改
能力提升内容拓展 1.根据下列条件写出抛物线的标准方程(1)焦点是F(3,0);(2)准线方程是x=1/4;(3)焦点到准线的距离是2;2.求下列抛物线的焦点坐标与准线方程(1)y2=28x; (2)4x2=y; (3)2y2+x=0;已知抛物线经过点(-4,-2),求它的标准方程 此题对学生思维水平要求较高,针对学生素质的差异,使学有余力的同学有所提高,从而达到“拔尖”的目的
课堂小结 教学内容1,抛物线的定义2,抛物线的标准方程3,标准方程的应用数学思想:数形结合思想分类讨论的思想解题方法:待定系数法
本课作业
板书设计
标准方程 图形 焦点 准线
EMBED Equation.DSMT4
EMBED Equation.DSMT4
