人教版数学七年级上册 第4章 4.1几何图形同步测试题(一)(Word版 含解析)
文档属性
| 名称 | 人教版数学七年级上册 第4章 4.1几何图形同步测试题(一)(Word版 含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 81.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-17 00:00:00 | ||
图片预览



文档简介
几何图形同步测试题(一)
一.选择题
1.用平面截一个正方体,所得截面不可能的是( )
A.圆
B.长方形
C.等腰三角形
D.梯形
2.下面几何体的截面图不可能是圆的是( )
A.棱柱
B.圆柱
C.圆锥
D.球
3.下列几何体,用一个平面去截,不能截得三角形截面的是( )
A.圆柱
B.圆锥
C.三棱柱
D.正方体
4.下列描述正确的是( )
A.单项式﹣的系数是﹣
B.圆柱的截面的形状可能是一个长方形
C.过七边形的一个顶点有7条对角线
D.五棱柱有5个面,15条棱
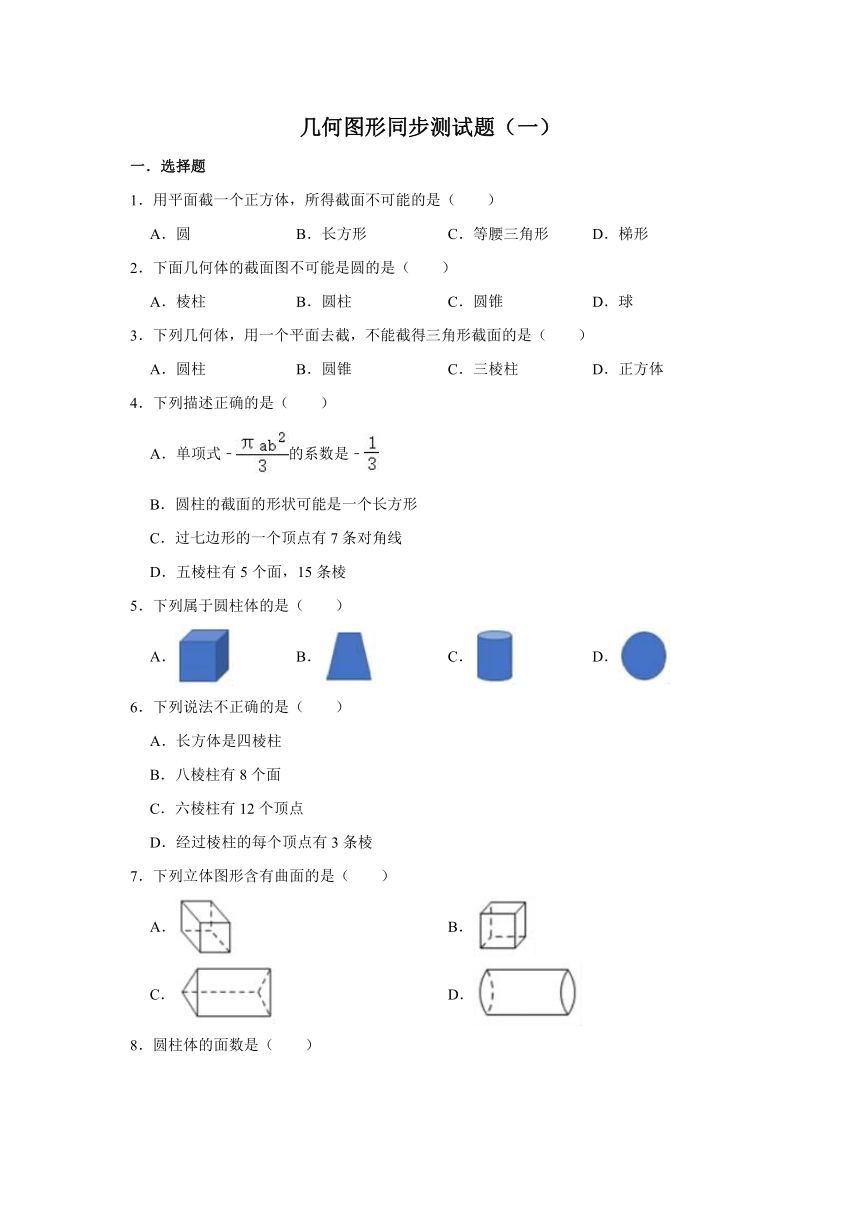
5.下列属于圆柱体的是( )
A.
B.
C.
D.
6.下列说法不正确的是( )
A.长方体是四棱柱
B.八棱柱有8个面
C.六棱柱有12个顶点
D.经过棱柱的每个顶点有3条棱
7.下列立体图形含有曲面的是( )
A.
B.
C.
D.
8.圆柱体的面数是( )
A.1
B.2
C.3
D.4
9.如图所示的是一个正方体的平面展开图,若将平面展开图折叠成正方体后,相对面上的两个数字之和均为7,期x+y+z的值为( )
A.7
B.8
C.9
D.10
10.如图,圆环中内圆的半径为a米,外圆半径比内圆半径长1米,那么外圆周长比内圆周长长( )
A.2π米
B.米
D.π米
二.填空题
11.在一个六棱柱中,共
有条棱.
12.
个完全相同的圆锥形铁块,可以熔铸成一个与它们等底等高的圆柱.
13.一个棱柱有16个顶点,则这个棱柱有
个面,有
条棱.
14.澳大利亚山火、西班牙大暴雪、菲律宾火山喷发、东非蝗灾、新型冠状病毒等灾难,都在给人类敲响警钟,我们要学会敬畏自然,尊重生命,与自然和谐共生,小明制作了如图所示的硬纸卡片,剪去一个小正方形后,使得剩余部分恰好能折成一个正方体,则剪去的小正方形可以是
.
15.一个长方形的长AB为4cm,宽BC为3cm,则将其绕AB边旋转一周,得到一个圆柱体,则该圆柱体的体积是
cm3(保留π).
三.解答题
16.计算下面圆锥的体积.
17.把一个长方形绕它的一条边所在的直线旋转一周能得到一个圆柱体,那么把一个长为4cm,宽为3cm的长方形绕它的一条边所在的直线旋转一周后,得到的圆柱体的体积是多少?(结果保留π)
18.一个圆柱的底面半径是10cm,高是18cm,把这个圆柱放在水平桌面上,如图所示.
(1)如果用一个平面沿水平方向去截这个圆柱,所得的截面是什么形状?
(2)如果用一个平面沿竖直方向去截这个圆柱,所得的截面是什么形状?
(3)怎样截时所得的截面是长方形且长方形的面积最大,请你求出这个截面面积.
19.如图.已知大圆的直径为4厘米,求图中空白部分的面积.
参考答案与试题解析
一.选择题
1.【解答】解:正方体有六个面,用平面去截正方体时最多与六个面相交得六边形,最少与三个面相交得三角形,所以截面可能为三角形、四边形(梯形,矩形,正方形)、五边形、六边形,而不可能是圆.
故选:A.
2.【解答】解:本题中,用平面去截棱柱,得的截面可能为多边形,无论如何,截面也不可能是圆.
故选:A.
3.【解答】解:用一个平面截一个几何体,不能截得三角形的截面的几何体有圆柱.
故选:A.
4.【解答】解:A、单项式﹣的系数是﹣π,故A错误;
B、用一个平面去截一个圆柱,截面的形状可能是一个长方形,故B正确;
C、过七边形的一个顶点有4条对角线,故C错误;
D、五棱柱有7个面,15条棱,故D错误.
故选:B.
5.【解答】解:A、图形是正方体,不符合题意;
B、图形是梯形,不符合题意;
C、图形属于圆柱体,符合题意;
D、图形是圆,不符合题意;
故选:C.
6.【解答】解:A、长方体是四棱柱,选项说法正确,不符合题意;
B、八棱柱有8+2=10个面,选项说法错误,符合题意;
C、六棱柱有2×6=12个顶点,选项说法正确,不符合题意;
D、经过棱柱的每个顶点有3条棱,选项说法正确,不符合题意;
故选:B.
7.【解答】解:棱柱的面都是平面,而圆柱的侧面是弯曲的面,
故选:D.
8.【解答】解:圆柱体是由两个圆形的底面,和一个弯曲的侧面围成的,
因此圆柱体是由三个面围成的,
故选:C.
9.【解答】解:根据正方体展开图的“相间、Z端是对面”的特征可知,
“﹣2”与“y”相对,
“3”与“z”相对,
“x”与“10”相对,
又∵相对面上的两个数字之和均为7,
∴x=﹣3,y=9,z=4,
∴x+y+z=﹣3+9+4=10,
故选:D.
10.【解答】解:内圆的周长为2πα米,外圆的周长为2π(a+1)米,
2π(a+1)﹣2πa=2π米,
故选:A.
二.填空题(共5小题)
11.【解答】解:在一个六棱柱中,共有3×6=18条棱,
故答案为:18.
12.【解答】解:因为圆柱的体积是同底同高的圆锥的体积的三倍,
所以3个完全相同的圆锥形铁块,可以熔铸成一个与它们等底等高的圆柱.
故答案为:3.
13.【解答】解:∵棱柱有16个顶点,
∴这个棱柱是八棱柱,
∴八棱柱有8+2=10个面,有8×3=24条棱,
故答案为:10,24.
14.【解答】解:∵剩余的部分恰好能折成一个正方体,
∴展开图中没有田字形,
∴应剪去与或自或然的小正方形.
故答案为:与或自或然.
15.【解答】解:由题意得,绕AB边旋转一周,得到的圆柱体的底面半径为3cm,高为4cm,
因此体积为π×32×4=36π(cm3),
故答案为:36π.
三.解答题(共4小题)
16.【解答】解:圆锥的体积:=(cm3).
17.【解答】解:绕长所在的直线旋转一周得到圆柱体积为:
π×32×4=36π(cm3),
绕宽所在的直线旋转一周得到圆柱体积为:
π×42×3=48π(cm3),
答:得到的圆柱体的体积是36πcm3或者48πcm3.
18.【解答】解:(1)所得的截面是圆;
(2)所得的截面是长方形;
(3)当平面沿竖直方向且经过两个底面的圆心时,截得的长方形面积最大,
这时,长方形的一边等于圆柱的高,长方形的另一边等于圆柱的底面直径,
则这个长方形的面积为:10×2×18=360(cm2).
19.【解答】解:如图,通过割补法,空白部分的面积可以转化为正方形ACBD的面积,
S正方形ACBD=ABCD=×4×4=8(cm2),
答:图中空白部分的面积为8cm2.
一.选择题
1.用平面截一个正方体,所得截面不可能的是( )
A.圆
B.长方形
C.等腰三角形
D.梯形
2.下面几何体的截面图不可能是圆的是( )
A.棱柱
B.圆柱
C.圆锥
D.球
3.下列几何体,用一个平面去截,不能截得三角形截面的是( )
A.圆柱
B.圆锥
C.三棱柱
D.正方体
4.下列描述正确的是( )
A.单项式﹣的系数是﹣
B.圆柱的截面的形状可能是一个长方形
C.过七边形的一个顶点有7条对角线
D.五棱柱有5个面,15条棱
5.下列属于圆柱体的是( )
A.
B.
C.
D.
6.下列说法不正确的是( )
A.长方体是四棱柱
B.八棱柱有8个面
C.六棱柱有12个顶点
D.经过棱柱的每个顶点有3条棱
7.下列立体图形含有曲面的是( )
A.
B.
C.
D.
8.圆柱体的面数是( )
A.1
B.2
C.3
D.4
9.如图所示的是一个正方体的平面展开图,若将平面展开图折叠成正方体后,相对面上的两个数字之和均为7,期x+y+z的值为( )
A.7
B.8
C.9
D.10
10.如图,圆环中内圆的半径为a米,外圆半径比内圆半径长1米,那么外圆周长比内圆周长长( )
A.2π米
B.米
D.π米
二.填空题
11.在一个六棱柱中,共
有条棱.
12.
个完全相同的圆锥形铁块,可以熔铸成一个与它们等底等高的圆柱.
13.一个棱柱有16个顶点,则这个棱柱有
个面,有
条棱.
14.澳大利亚山火、西班牙大暴雪、菲律宾火山喷发、东非蝗灾、新型冠状病毒等灾难,都在给人类敲响警钟,我们要学会敬畏自然,尊重生命,与自然和谐共生,小明制作了如图所示的硬纸卡片,剪去一个小正方形后,使得剩余部分恰好能折成一个正方体,则剪去的小正方形可以是
.
15.一个长方形的长AB为4cm,宽BC为3cm,则将其绕AB边旋转一周,得到一个圆柱体,则该圆柱体的体积是
cm3(保留π).
三.解答题
16.计算下面圆锥的体积.
17.把一个长方形绕它的一条边所在的直线旋转一周能得到一个圆柱体,那么把一个长为4cm,宽为3cm的长方形绕它的一条边所在的直线旋转一周后,得到的圆柱体的体积是多少?(结果保留π)
18.一个圆柱的底面半径是10cm,高是18cm,把这个圆柱放在水平桌面上,如图所示.
(1)如果用一个平面沿水平方向去截这个圆柱,所得的截面是什么形状?
(2)如果用一个平面沿竖直方向去截这个圆柱,所得的截面是什么形状?
(3)怎样截时所得的截面是长方形且长方形的面积最大,请你求出这个截面面积.
19.如图.已知大圆的直径为4厘米,求图中空白部分的面积.
参考答案与试题解析
一.选择题
1.【解答】解:正方体有六个面,用平面去截正方体时最多与六个面相交得六边形,最少与三个面相交得三角形,所以截面可能为三角形、四边形(梯形,矩形,正方形)、五边形、六边形,而不可能是圆.
故选:A.
2.【解答】解:本题中,用平面去截棱柱,得的截面可能为多边形,无论如何,截面也不可能是圆.
故选:A.
3.【解答】解:用一个平面截一个几何体,不能截得三角形的截面的几何体有圆柱.
故选:A.
4.【解答】解:A、单项式﹣的系数是﹣π,故A错误;
B、用一个平面去截一个圆柱,截面的形状可能是一个长方形,故B正确;
C、过七边形的一个顶点有4条对角线,故C错误;
D、五棱柱有7个面,15条棱,故D错误.
故选:B.
5.【解答】解:A、图形是正方体,不符合题意;
B、图形是梯形,不符合题意;
C、图形属于圆柱体,符合题意;
D、图形是圆,不符合题意;
故选:C.
6.【解答】解:A、长方体是四棱柱,选项说法正确,不符合题意;
B、八棱柱有8+2=10个面,选项说法错误,符合题意;
C、六棱柱有2×6=12个顶点,选项说法正确,不符合题意;
D、经过棱柱的每个顶点有3条棱,选项说法正确,不符合题意;
故选:B.
7.【解答】解:棱柱的面都是平面,而圆柱的侧面是弯曲的面,
故选:D.
8.【解答】解:圆柱体是由两个圆形的底面,和一个弯曲的侧面围成的,
因此圆柱体是由三个面围成的,
故选:C.
9.【解答】解:根据正方体展开图的“相间、Z端是对面”的特征可知,
“﹣2”与“y”相对,
“3”与“z”相对,
“x”与“10”相对,
又∵相对面上的两个数字之和均为7,
∴x=﹣3,y=9,z=4,
∴x+y+z=﹣3+9+4=10,
故选:D.
10.【解答】解:内圆的周长为2πα米,外圆的周长为2π(a+1)米,
2π(a+1)﹣2πa=2π米,
故选:A.
二.填空题(共5小题)
11.【解答】解:在一个六棱柱中,共有3×6=18条棱,
故答案为:18.
12.【解答】解:因为圆柱的体积是同底同高的圆锥的体积的三倍,
所以3个完全相同的圆锥形铁块,可以熔铸成一个与它们等底等高的圆柱.
故答案为:3.
13.【解答】解:∵棱柱有16个顶点,
∴这个棱柱是八棱柱,
∴八棱柱有8+2=10个面,有8×3=24条棱,
故答案为:10,24.
14.【解答】解:∵剩余的部分恰好能折成一个正方体,
∴展开图中没有田字形,
∴应剪去与或自或然的小正方形.
故答案为:与或自或然.
15.【解答】解:由题意得,绕AB边旋转一周,得到的圆柱体的底面半径为3cm,高为4cm,
因此体积为π×32×4=36π(cm3),
故答案为:36π.
三.解答题(共4小题)
16.【解答】解:圆锥的体积:=(cm3).
17.【解答】解:绕长所在的直线旋转一周得到圆柱体积为:
π×32×4=36π(cm3),
绕宽所在的直线旋转一周得到圆柱体积为:
π×42×3=48π(cm3),
答:得到的圆柱体的体积是36πcm3或者48πcm3.
18.【解答】解:(1)所得的截面是圆;
(2)所得的截面是长方形;
(3)当平面沿竖直方向且经过两个底面的圆心时,截得的长方形面积最大,
这时,长方形的一边等于圆柱的高,长方形的另一边等于圆柱的底面直径,
则这个长方形的面积为:10×2×18=360(cm2).
19.【解答】解:如图,通过割补法,空白部分的面积可以转化为正方形ACBD的面积,
S正方形ACBD=ABCD=×4×4=8(cm2),
答:图中空白部分的面积为8cm2.
