人教版数学七年级上册 第4章 4.3角同步练习试题(一)(Word版 含解析)
文档属性
| 名称 | 人教版数学七年级上册 第4章 4.3角同步练习试题(一)(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 126.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-17 20:13:20 | ||
图片预览



文档简介
角同步练习试题(一)
一.选择题
1.小明从A处出发沿北偏东60°方向行走至B处,又沿北偏西25°方向行走至C处,此时需把方向调整到与出发时一致,则方向的调整应是( )
A.左转85°
B.右转85°
C.右转95°
D.左转95°
2.钟表上12时15分时,时针和分针的夹角是( )
A.120°
B.90°
C.82.5°
D.60°
3.下列说法正确的是( )
A.在所有连接两点的线中,直线最短
B.一个角的余角一定比这个角大
C.同角(或等角)的补角相等
D.经过两点有无数条直线
4.如图,点A、B分别是∠NOP、∠MOP平分线上的点,AB⊥OP于点E,BC⊥MN于点C,AD⊥MN于点D,下列结论错误的是( )
A.AD+BC=AB
B.与∠CBO互余的角有两个
C.∠AOB=90°
D.点O是CD的中点
5.下列说法中错误的有( )
(1)线段有两个端点;
(2)角的大小与我们画出的角的两边的长短无关;
(3)线段上有无数个点;
(4)同角或等角的补角相等;
(5)两个锐角的和一定大于直角.
A.1个
B.2个
C.3个
D.4个
6.若一个角为75°,则它的补角的度数为( )
A.35°
B.45°
C.105°
D.115°
7.α、β都是钝角,甲、乙、丙、丁四位同学计算(α+β)的结果依次为50°、26°、72°和90°,其中有正确的结果,那么算得正确的是( )
A.甲
B.乙
C.丙
D.丁
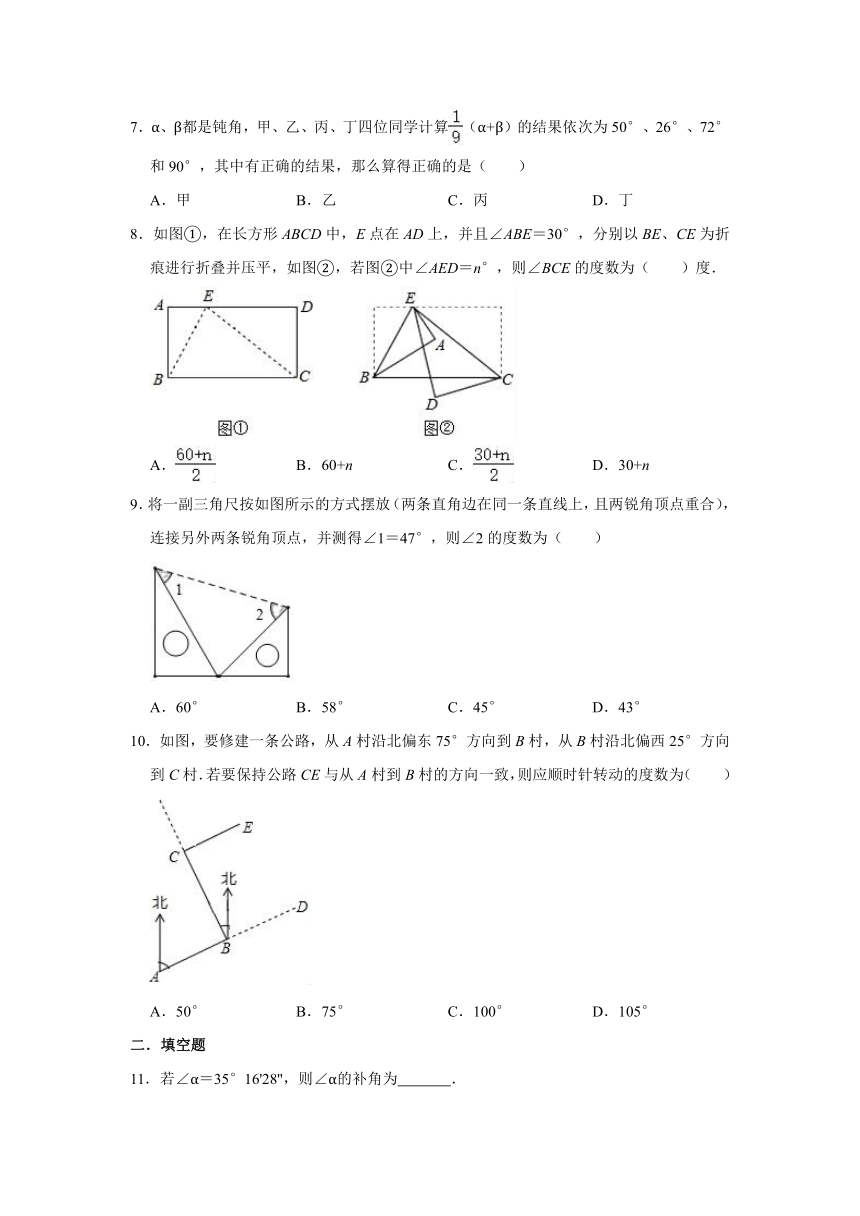
8.如图①,在长方形ABCD中,E点在AD上,并且∠ABE=30°,分别以BE、CE为折痕进行折叠并压平,如图②,若图②中∠AED=n°,则∠BCE的度数为( )度.
A.
B.60+n
C.
D.30+n
9.将一副三角尺按如图所示的方式摆放(两条直角边在同一条直线上,且两锐角顶点重合),连接另外两条锐角顶点,并测得∠1=47°,则∠2的度数为( )
A.60°
B.58°
C.45°
D.43°
10.如图,要修建一条公路,从A村沿北偏东75°方向到B村,从B村沿北偏西25°方向到C村.若要保持公路CE与从A村到B村的方向一致,则应顺时针转动的度数为( )
A.50°
B.75°
C.100°
D.105°
二.填空题
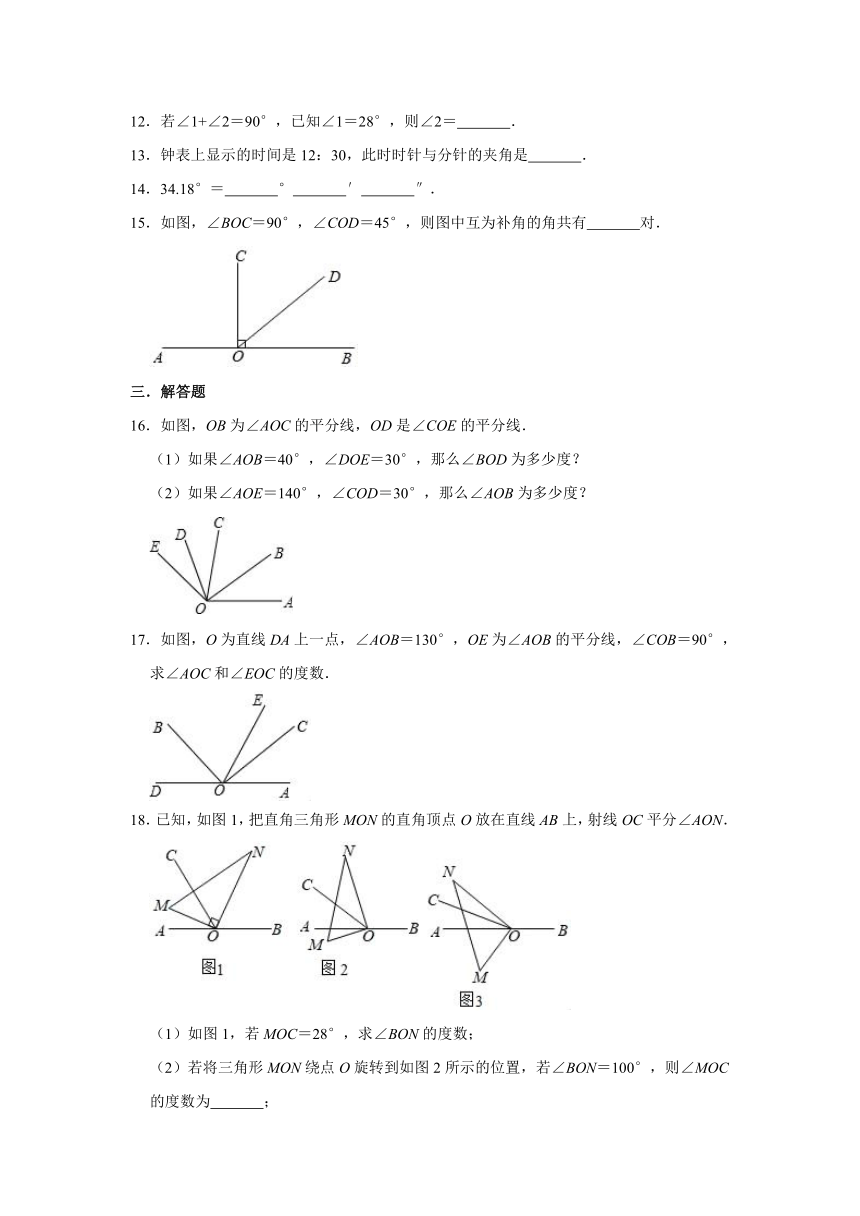
11.若∠α=35°16'28'',则∠α的补角为
.
12.若∠1+∠2=90°,已知∠1=28°,则∠2=
.
13.钟表上显示的时间是12:30,此时时针与分针的夹角是
.
14.34.18°=
°
′
″.
15.如图,∠BOC=90°,∠COD=45°,则图中互为补角的角共有
对.
三.解答题
16.如图,OB为∠AOC的平分线,OD是∠COE的平分线.
(1)如果∠AOB=40°,∠DOE=30°,那么∠BOD为多少度?
(2)如果∠AOE=140°,∠COD=30°,那么∠AOB为多少度?
17.如图,O为直线DA上一点,∠AOB=130°,OE为∠AOB的平分线,∠COB=90°,求∠AOC和∠EOC的度数.
18.已知,如图1,把直角三角形MON的直角顶点O放在直线AB上,射线OC平分∠AON.
(1)如图1,若MOC=28°,求∠BON的度数;
(2)若将三角形MON绕点O旋转到如图2所示的位置,若∠BON=100°,则∠MOC的度数为
;
(3)若将三角形MON绕点O旋转到如图3所示的位置,试写出∠BON和∠MOC之间的数量关系,并说明理由.
19.如图1,将一副三角板的直角顶点C叠放在一起.观察分析:
(1)若∠DCE=35°,则∠ACB=
;
若∠ACB=150°,则∠DCE=
;
猜想探究:
(2)请你猜想∠ACB与∠DCE有何关系,并说明理由;
拓展应用:
(3)如图2,若将两个同样的三角尺60°锐角的顶点A重合在一起,请你猜想∠DAB与∠CAE有何关系,请说明理由;
(4)如图3,如果把任意两个锐角∠AOB、∠COD的顶点O重合在一起,已知∠AOB=α,∠COD=β(α、β都是锐角),请你直接写出∠AOD与∠BOC的关系.
参考答案与试题解析
一.选择题
1.【解答】解:如图:
60°+25°=85°.
由北偏西25°转向北偏东60°,需要向右转85°.
故选:B.
2.【解答】解:∵时针在钟面上每分钟转0.5°,分针每分钟转6°,
∴钟表上12时15分钟时,时针与分针的夹角可以看成时针转过12时0.5°×15=7.5°,分针在数字3上.
∵钟表12个数字,每相邻两个数字之间的夹角为30°,
∴12时15分钟时分针与时针的夹角90°﹣7.5°=82.5°.
故选:C.
3.【解答】解:A、在所有连接两点的线中,线段最短,故原说法错误,故本选项不合题意;
B、一个角的余角不一定比这个角大,如60°角的余角是30°,故原说法错误,故本选项不合题意;
C、同角(或等角)的补角相等,说法正确,故本选项符合题意;
D、经过两点有且只有一条直线,故原说法错误,故本选项不合题意;
故选:C.
4.【解答】解:∵点A,B分别是∠NOP,∠MOP平分线上的点,
∴AD=AE,BC=BE,
∵AB=AE+BE,
∴AB=AD+BC,故A选项结论正确;
在Rt△AOD和Rt△AOE中,
,
∴Rt△AOD≌Rt△AOE(HL),
∴OD=OE,∠AOE=∠AOD,
同理可得OC=OE,∠BOC=∠BOE,
∴∠AOB=×180°=90°,故C选项结论正确;
∵BC⊥MN,
∴∠CBO+∠COB=90°;
∵点A、B分别是∠NOP、∠MOP平分线上的点,
∴∠COB=∠EOB,∠AOD=∠AOE,
∴∠BOE+∠AOE=90°,∠EOB+∠AOE=90°,
∴∠CBO+∠EOB=90°,
∵AB⊥OP于点E,AD⊥MN于点D,
∴∠AOE+∠OAD=90°,∠AOD+∠OAE=90°,
∴∠CBO+∠OAD=90°,∠CBO+∠OAE=90°,
与∠CBO互余的角有∠COB,∠EOB,∠OAD,∠OAE共4个,故B选项结论错误;
∵OC=OD=OE,
∴点O是CD的中点,故D选项结论正确.
故选:B.
5.【解答】解:(1)线段有两个端点,原说法正确;
(2)角的大小与我们画出的角的两边的长短无关,原说法正确;
(3)线段上有无数个点,原说法正确;
(4)同角或等角的补角相等,原说法正确;
(5)两个锐角的和不一定大于直角,原说法错误.
错误的有1个,
故选:A.
6.【解答】解:180°﹣75°=105°
则其补角为105°.
故选:C.
7.【解答】解:∵α、β都是钝角,
∴90°<α<180°,90°<β<180°,
∴20°<(α+β)<40°,
∴26°在此范围内,
故选:B.
8.【解答】解:折叠后的图形如下:
∵∠ABE=30°,
∴∠BEA'=∠BAE=60°,
又∵A'D'∥BC,
∴∠BCE=∠CED',
又∵∠CED'=∠CED,
∴∠BCE=∠CED'=∠CED,
又∵∠DEC=∠DED',
∴∠DEC=(180°﹣∠A'EA+∠AED)
=(180°﹣120°+n°)
=(30+)°
∴∠BCE=(30+)°
故选:A.
9.【解答】解:如图所示,
∠3=180°﹣60°﹣45°=75°,
则∠2=180°﹣∠1﹣∠3=180°﹣47°﹣75°=58°.
故选:B.
10.【解答】解:由题意可得:AN∥FB,DC∥BE,
∴∠NAB=∠FBE=75°,
∵∠CBF=25°,
∴∠CBE=100°,
则应顺时针转动的度数为100°.
故选:C.
二.填空题(共5小题)
11.【解答】解:∵∠α=35°16'28'',
∴∠α的补角=180°﹣35°16'28''=144°43′32″.
故答案为:144°43′32″.
12.【解答】解:∵∠1+∠2=90°,∠1=28°,
∴∠2=90°﹣∠1=90°﹣28°=62°.
故答案为:62°.
13.【解答】解:12:30时,时针与分针相距5.5份,
夹角为30°×5.5=165°,
故选:165°.
14.【解答】解:0.18°×60=10.8′,0.8′×60=48″,所以34.18°=34°10′48″.
故答案是:34;10;48.
15.【解答】解:∵∠BOC=90°,
∴∠AOC=∠BOC=90°,
∴∠AOC与∠BOC互为补角;
∵∠BOD+∠AOD=180°,
∴∠AOD与∠BOD互为补角;
∵∠COD=45°,
∴∠BOD=45°,
∴∠AOD与∠COD互为补角;
∴图中互为补角的角共有3对,
故答案为:3.
三.解答题(共4小题)
16.【解答】解:(1)如图,∵OB为∠AOC的平分线,OD是∠COE的平分线,
∴∠AOB=∠BOC,∠DOE=∠DOC,
∴∠BOD=∠BOC+∠DOC=∠AOB+∠DOE=40°+30°=70°;
(2)如图,∵OD是∠COE的平分线,∠COD=30°,
∴∠EOC=2∠COD=60°.
∵∠AOE=140°,∠AOC=∠AOE﹣∠EOC=80°.
又∵OB为∠AOC的平分线,
∴∠AOB=∠AOC=40°.
17.【解答】解:因为∠AOB=130°,OE是∠AOB的平分线,
所以∠BOE=,
因为∠COB=90°,
所以∠COE=90°﹣65°=25°,
所以∠AOC=∠AOE﹣∠COE=65°﹣25°=40°.
18.【解答】解:(1)如图1,∵∠MOC=28°,∠MON=90°,
∴∠NOC=90°﹣28°=62°,
又∵OC平分∠AON,
∴∠AOC=∠NOC=62°,
∴∠BON=180°﹣2∠NOC=180°﹣62°×2=56°;
(2)∵∠BON=100°,
∴∠AON=80°,
∴∠AOM=90°﹣∠AON=10°,∠AOC=40°,
∴∠MOC=∠AOM+∠AOC=50°.
故答案为:50°;
(3)∠MOC和∠BON之间的数量关系不发生变化,
如图2,∵OC平分∠AON,
∴∠AOC=∠NOC,
∵∠MON=90°,
∴∠AOC=∠NOC=90°﹣∠MOC,
∴∠BON=180°﹣2∠NOC=180°﹣2(90°﹣∠MOC)=2∠MOC,
即:∠BON=2∠MOC.
19.【解答】解:(1)(1)若∠DCE=35°,
∵∠ACD=90°,∠DCE=35°,
∴∠ACE=90°﹣35°=55°,
∵∠BCE=90°,
∴∠ACB=∠ACE+∠BCE=55°+90°=145°;
若∠ACB=150°,
∵∠BCE=90°,
∴∠ACE=150°﹣90°=60°,
∵∠ACD=90°,
∴∠DCE=90°﹣60°=30°,
故答案为:145°,30°;
(2)∠ACB+∠DCE=180°,
理由:∵∠ACE+∠ECD=90°,∠ECD+∠DCB=90°,
∴∠ACE+∠ECD+∠ECD+∠DCB=180°,
∵∠ACE+∠ECD+∠DCB=∠ACB,
∴∠ACB+∠ECD=180°;
(3)∠DAB+∠EAC=120°,
理由:∵∠DAE+∠EAC=60°,∠EAC+∠CAB=60°,
∴∠DAE+∠EAC+∠EAC+∠CAB=120°,
∵∠DAE+∠EAC+∠CAB=∠DAB,
∴∠DAB+∠EAC=120°;
(4)∠AOD+∠BOC=α+β,理由是:
∵∠AOD=∠DOC+∠COA=β+∠COA,
∴∠AOD+∠BOC=β+∠COA+∠BOC,
=β+∠AOB,
=α+β.
一.选择题
1.小明从A处出发沿北偏东60°方向行走至B处,又沿北偏西25°方向行走至C处,此时需把方向调整到与出发时一致,则方向的调整应是( )
A.左转85°
B.右转85°
C.右转95°
D.左转95°
2.钟表上12时15分时,时针和分针的夹角是( )
A.120°
B.90°
C.82.5°
D.60°
3.下列说法正确的是( )
A.在所有连接两点的线中,直线最短
B.一个角的余角一定比这个角大
C.同角(或等角)的补角相等
D.经过两点有无数条直线
4.如图,点A、B分别是∠NOP、∠MOP平分线上的点,AB⊥OP于点E,BC⊥MN于点C,AD⊥MN于点D,下列结论错误的是( )
A.AD+BC=AB
B.与∠CBO互余的角有两个
C.∠AOB=90°
D.点O是CD的中点
5.下列说法中错误的有( )
(1)线段有两个端点;
(2)角的大小与我们画出的角的两边的长短无关;
(3)线段上有无数个点;
(4)同角或等角的补角相等;
(5)两个锐角的和一定大于直角.
A.1个
B.2个
C.3个
D.4个
6.若一个角为75°,则它的补角的度数为( )
A.35°
B.45°
C.105°
D.115°
7.α、β都是钝角,甲、乙、丙、丁四位同学计算(α+β)的结果依次为50°、26°、72°和90°,其中有正确的结果,那么算得正确的是( )
A.甲
B.乙
C.丙
D.丁
8.如图①,在长方形ABCD中,E点在AD上,并且∠ABE=30°,分别以BE、CE为折痕进行折叠并压平,如图②,若图②中∠AED=n°,则∠BCE的度数为( )度.
A.
B.60+n
C.
D.30+n
9.将一副三角尺按如图所示的方式摆放(两条直角边在同一条直线上,且两锐角顶点重合),连接另外两条锐角顶点,并测得∠1=47°,则∠2的度数为( )
A.60°
B.58°
C.45°
D.43°
10.如图,要修建一条公路,从A村沿北偏东75°方向到B村,从B村沿北偏西25°方向到C村.若要保持公路CE与从A村到B村的方向一致,则应顺时针转动的度数为( )
A.50°
B.75°
C.100°
D.105°
二.填空题
11.若∠α=35°16'28'',则∠α的补角为
.
12.若∠1+∠2=90°,已知∠1=28°,则∠2=
.
13.钟表上显示的时间是12:30,此时时针与分针的夹角是
.
14.34.18°=
°
′
″.
15.如图,∠BOC=90°,∠COD=45°,则图中互为补角的角共有
对.
三.解答题
16.如图,OB为∠AOC的平分线,OD是∠COE的平分线.
(1)如果∠AOB=40°,∠DOE=30°,那么∠BOD为多少度?
(2)如果∠AOE=140°,∠COD=30°,那么∠AOB为多少度?
17.如图,O为直线DA上一点,∠AOB=130°,OE为∠AOB的平分线,∠COB=90°,求∠AOC和∠EOC的度数.
18.已知,如图1,把直角三角形MON的直角顶点O放在直线AB上,射线OC平分∠AON.
(1)如图1,若MOC=28°,求∠BON的度数;
(2)若将三角形MON绕点O旋转到如图2所示的位置,若∠BON=100°,则∠MOC的度数为
;
(3)若将三角形MON绕点O旋转到如图3所示的位置,试写出∠BON和∠MOC之间的数量关系,并说明理由.
19.如图1,将一副三角板的直角顶点C叠放在一起.观察分析:
(1)若∠DCE=35°,则∠ACB=
;
若∠ACB=150°,则∠DCE=
;
猜想探究:
(2)请你猜想∠ACB与∠DCE有何关系,并说明理由;
拓展应用:
(3)如图2,若将两个同样的三角尺60°锐角的顶点A重合在一起,请你猜想∠DAB与∠CAE有何关系,请说明理由;
(4)如图3,如果把任意两个锐角∠AOB、∠COD的顶点O重合在一起,已知∠AOB=α,∠COD=β(α、β都是锐角),请你直接写出∠AOD与∠BOC的关系.
参考答案与试题解析
一.选择题
1.【解答】解:如图:
60°+25°=85°.
由北偏西25°转向北偏东60°,需要向右转85°.
故选:B.
2.【解答】解:∵时针在钟面上每分钟转0.5°,分针每分钟转6°,
∴钟表上12时15分钟时,时针与分针的夹角可以看成时针转过12时0.5°×15=7.5°,分针在数字3上.
∵钟表12个数字,每相邻两个数字之间的夹角为30°,
∴12时15分钟时分针与时针的夹角90°﹣7.5°=82.5°.
故选:C.
3.【解答】解:A、在所有连接两点的线中,线段最短,故原说法错误,故本选项不合题意;
B、一个角的余角不一定比这个角大,如60°角的余角是30°,故原说法错误,故本选项不合题意;
C、同角(或等角)的补角相等,说法正确,故本选项符合题意;
D、经过两点有且只有一条直线,故原说法错误,故本选项不合题意;
故选:C.
4.【解答】解:∵点A,B分别是∠NOP,∠MOP平分线上的点,
∴AD=AE,BC=BE,
∵AB=AE+BE,
∴AB=AD+BC,故A选项结论正确;
在Rt△AOD和Rt△AOE中,
,
∴Rt△AOD≌Rt△AOE(HL),
∴OD=OE,∠AOE=∠AOD,
同理可得OC=OE,∠BOC=∠BOE,
∴∠AOB=×180°=90°,故C选项结论正确;
∵BC⊥MN,
∴∠CBO+∠COB=90°;
∵点A、B分别是∠NOP、∠MOP平分线上的点,
∴∠COB=∠EOB,∠AOD=∠AOE,
∴∠BOE+∠AOE=90°,∠EOB+∠AOE=90°,
∴∠CBO+∠EOB=90°,
∵AB⊥OP于点E,AD⊥MN于点D,
∴∠AOE+∠OAD=90°,∠AOD+∠OAE=90°,
∴∠CBO+∠OAD=90°,∠CBO+∠OAE=90°,
与∠CBO互余的角有∠COB,∠EOB,∠OAD,∠OAE共4个,故B选项结论错误;
∵OC=OD=OE,
∴点O是CD的中点,故D选项结论正确.
故选:B.
5.【解答】解:(1)线段有两个端点,原说法正确;
(2)角的大小与我们画出的角的两边的长短无关,原说法正确;
(3)线段上有无数个点,原说法正确;
(4)同角或等角的补角相等,原说法正确;
(5)两个锐角的和不一定大于直角,原说法错误.
错误的有1个,
故选:A.
6.【解答】解:180°﹣75°=105°
则其补角为105°.
故选:C.
7.【解答】解:∵α、β都是钝角,
∴90°<α<180°,90°<β<180°,
∴20°<(α+β)<40°,
∴26°在此范围内,
故选:B.
8.【解答】解:折叠后的图形如下:
∵∠ABE=30°,
∴∠BEA'=∠BAE=60°,
又∵A'D'∥BC,
∴∠BCE=∠CED',
又∵∠CED'=∠CED,
∴∠BCE=∠CED'=∠CED,
又∵∠DEC=∠DED',
∴∠DEC=(180°﹣∠A'EA+∠AED)
=(180°﹣120°+n°)
=(30+)°
∴∠BCE=(30+)°
故选:A.
9.【解答】解:如图所示,
∠3=180°﹣60°﹣45°=75°,
则∠2=180°﹣∠1﹣∠3=180°﹣47°﹣75°=58°.
故选:B.
10.【解答】解:由题意可得:AN∥FB,DC∥BE,
∴∠NAB=∠FBE=75°,
∵∠CBF=25°,
∴∠CBE=100°,
则应顺时针转动的度数为100°.
故选:C.
二.填空题(共5小题)
11.【解答】解:∵∠α=35°16'28'',
∴∠α的补角=180°﹣35°16'28''=144°43′32″.
故答案为:144°43′32″.
12.【解答】解:∵∠1+∠2=90°,∠1=28°,
∴∠2=90°﹣∠1=90°﹣28°=62°.
故答案为:62°.
13.【解答】解:12:30时,时针与分针相距5.5份,
夹角为30°×5.5=165°,
故选:165°.
14.【解答】解:0.18°×60=10.8′,0.8′×60=48″,所以34.18°=34°10′48″.
故答案是:34;10;48.
15.【解答】解:∵∠BOC=90°,
∴∠AOC=∠BOC=90°,
∴∠AOC与∠BOC互为补角;
∵∠BOD+∠AOD=180°,
∴∠AOD与∠BOD互为补角;
∵∠COD=45°,
∴∠BOD=45°,
∴∠AOD与∠COD互为补角;
∴图中互为补角的角共有3对,
故答案为:3.
三.解答题(共4小题)
16.【解答】解:(1)如图,∵OB为∠AOC的平分线,OD是∠COE的平分线,
∴∠AOB=∠BOC,∠DOE=∠DOC,
∴∠BOD=∠BOC+∠DOC=∠AOB+∠DOE=40°+30°=70°;
(2)如图,∵OD是∠COE的平分线,∠COD=30°,
∴∠EOC=2∠COD=60°.
∵∠AOE=140°,∠AOC=∠AOE﹣∠EOC=80°.
又∵OB为∠AOC的平分线,
∴∠AOB=∠AOC=40°.
17.【解答】解:因为∠AOB=130°,OE是∠AOB的平分线,
所以∠BOE=,
因为∠COB=90°,
所以∠COE=90°﹣65°=25°,
所以∠AOC=∠AOE﹣∠COE=65°﹣25°=40°.
18.【解答】解:(1)如图1,∵∠MOC=28°,∠MON=90°,
∴∠NOC=90°﹣28°=62°,
又∵OC平分∠AON,
∴∠AOC=∠NOC=62°,
∴∠BON=180°﹣2∠NOC=180°﹣62°×2=56°;
(2)∵∠BON=100°,
∴∠AON=80°,
∴∠AOM=90°﹣∠AON=10°,∠AOC=40°,
∴∠MOC=∠AOM+∠AOC=50°.
故答案为:50°;
(3)∠MOC和∠BON之间的数量关系不发生变化,
如图2,∵OC平分∠AON,
∴∠AOC=∠NOC,
∵∠MON=90°,
∴∠AOC=∠NOC=90°﹣∠MOC,
∴∠BON=180°﹣2∠NOC=180°﹣2(90°﹣∠MOC)=2∠MOC,
即:∠BON=2∠MOC.
19.【解答】解:(1)(1)若∠DCE=35°,
∵∠ACD=90°,∠DCE=35°,
∴∠ACE=90°﹣35°=55°,
∵∠BCE=90°,
∴∠ACB=∠ACE+∠BCE=55°+90°=145°;
若∠ACB=150°,
∵∠BCE=90°,
∴∠ACE=150°﹣90°=60°,
∵∠ACD=90°,
∴∠DCE=90°﹣60°=30°,
故答案为:145°,30°;
(2)∠ACB+∠DCE=180°,
理由:∵∠ACE+∠ECD=90°,∠ECD+∠DCB=90°,
∴∠ACE+∠ECD+∠ECD+∠DCB=180°,
∵∠ACE+∠ECD+∠DCB=∠ACB,
∴∠ACB+∠ECD=180°;
(3)∠DAB+∠EAC=120°,
理由:∵∠DAE+∠EAC=60°,∠EAC+∠CAB=60°,
∴∠DAE+∠EAC+∠EAC+∠CAB=120°,
∵∠DAE+∠EAC+∠CAB=∠DAB,
∴∠DAB+∠EAC=120°;
(4)∠AOD+∠BOC=α+β,理由是:
∵∠AOD=∠DOC+∠COA=β+∠COA,
∴∠AOD+∠BOC=β+∠COA+∠BOC,
=β+∠AOB,
=α+β.
