人教版数学七年级下册 第7章 7.1平面直角坐标系同步测试试题(一)(Word版 含解析)
文档属性
| 名称 | 人教版数学七年级下册 第7章 7.1平面直角坐标系同步测试试题(一)(Word版 含解析) | 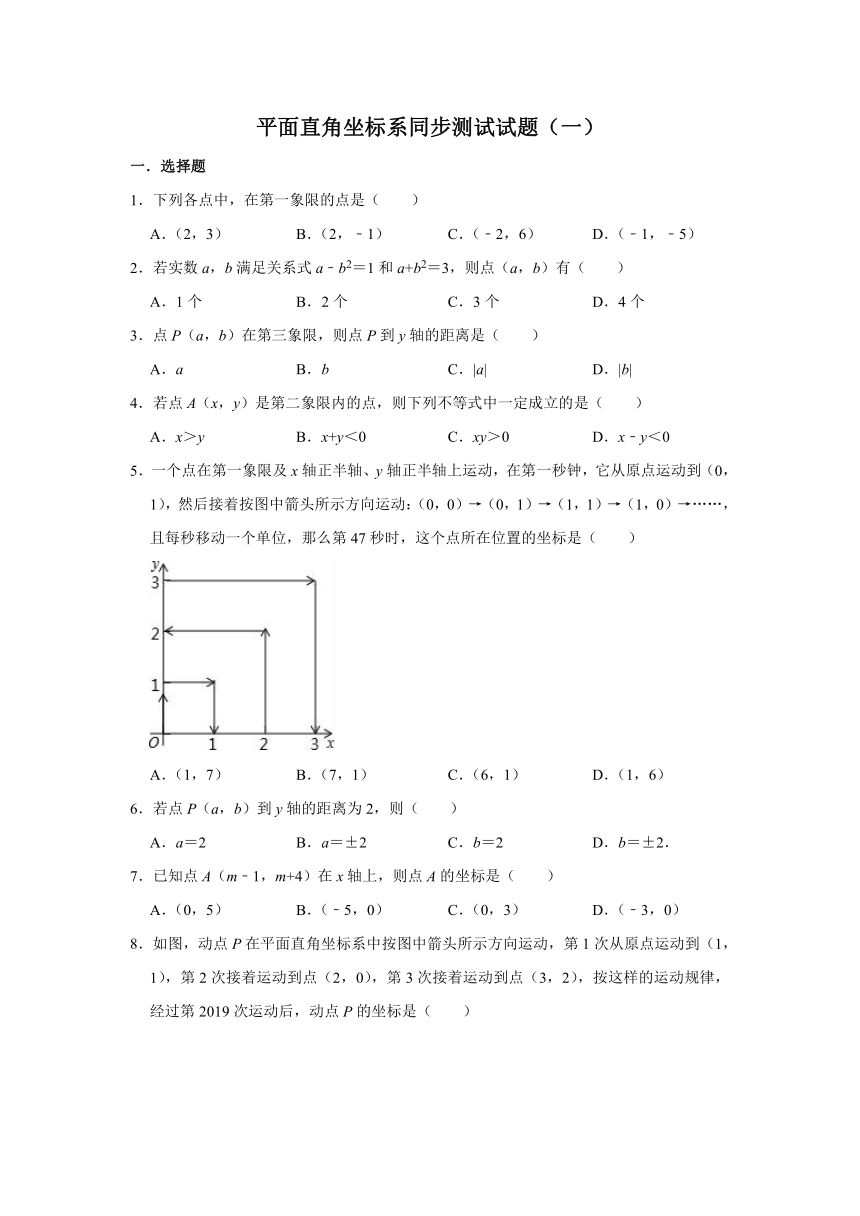 | |
| 格式 | zip | ||
| 文件大小 | 60.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-17 20:05:51 | ||
图片预览




文档简介
平面直角坐标系同步测试试题(一)
一.选择题
1.下列各点中,在第一象限的点是( )
A.(2,3)
B.(2,﹣1)
C.(﹣2,6)
D.(﹣1,﹣5)
2.若实数a,b满足关系式a﹣b2=1和a+b2=3,则点(a,b)有( )
A.1个
B.2个
C.3个
D.4个
3.点P(a,b)在第三象限,则点P到y轴的距离是( )
A.a
B.b
C.|a|
D.|b|
4.若点A(x,y)是第二象限内的点,则下列不等式中一定成立的是( )
A.x>y
B.x+y<0
C.xy>0
D.x﹣y<0
5.一个点在第一象限及x轴正半轴、y轴正半轴上运动,在第一秒钟,它从原点运动到(0,1),然后接着按图中箭头所示方向运动:(0,0)→(0,1)→(1,1)→(1,0)→……,且每秒移动一个单位,那么第47秒时,这个点所在位置的坐标是( )
A.(1,7)
B.(7,1)
C.(6,1)
D.(1,6)
6.若点P(a,b)到y轴的距离为2,则( )
A.a=2
B.a=±2
C.b=2
D.b=±2.
7.已知点A(m﹣1,m+4)在x轴上,则点A的坐标是( )
A.(0,5)
B.(﹣5,0)
C.(0,3)
D.(﹣3,0)
8.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),按这样的运动规律,经过第2019次运动后,动点P的坐标是( )
A.(2019,0)
B.(2019,1)
C.(2019,2)
D.(2020,0)
9.若点P(a,b)在第四象限,则( )
A.a>0,b>0
B.a<0,b<0
C.a<0,b>0
D.a>0,b<0
10.如图,笑脸盖住的点的坐标可能为( )
A.(5,2)
B.(﹣6,3)
C.(﹣4,﹣6)
D.(3,﹣4)
二.填空题
11.已知点P在第三象限,且点P到x轴的距离为3,到y轴的距离为2,那么点P的坐标为
.
12.如果点M(x,y)在第三象限,则xy的值
0.在第二象限,则点B(n,m)在第
象限.
14.点A在第二象限,它到x轴的距离是它到y轴距离的2倍,请写出一个满足条件的点A的坐标
.
15.对于平面坐标系中任意两点A(x1,y1),B(x2,y2)定义一种新运算“
”为:(x1,y1)
(x2,y2)=(x1y2,x2y1).若A(x1,y1)在第二象限,B(x2,y2)在第三象限,则A
B在第
象限.
三.解答题
16.已知点P(2x﹣6,3x+1)在y轴上,求P的坐标.
17.已知平面内点M(x,y),若x,y满足下列条件,请说出点M的位置.
(1)xy=0;
(2)>0.
18.平面直角坐标系中,有一点M(a﹣1,2a+7),试求满足下列条件的a的值.
(1)点M在x轴上;
(2)点M在第二象限;
(3)点M到y轴距离是1.
19.已知当m,n都是实数.且满足2m=8+n时,称p(m﹣1,)为“开心点”.
(1)判断点A(5,3),B(4,10)是否为“开心点”,并说明理由;
(2)若点M(a,2a﹣1)是“开心点”,请判断点M在第几象限?并说明理由.
参考答案与试题解析
一.选择题
1.【解答】解:A、(2,3),在第一象限,符合题意;
B、(2,﹣1)在第四象限,不合题意;
C、(﹣2,6)在第二象限,不合题意;
D、(﹣1,﹣5)在第三象限,不合题意.
故选:A.
2.【解答】解:∵a﹣b2=1和a+b2=3,
∴2a=4,
解得:a=2,
∴2﹣b2=1,
解得:b=±1,
∴点(a,b)有(2,1),(﹣2,1)共2个.
故选:B.
3.【解答】解:∵点P(a,b)在第三象限,
∴点P到y轴的距离是:|a|.
故选:C.
4.【解答】解:因为点A(x,y)是第二象限内的点,
所以x<0,y>0,
可得:x﹣y<0,x<y,xy<0,
故选:D.
5.【解答】解:这个点3秒时到了(1,0);8秒时到了(0,2);15秒时到了(3,0);24秒到了(0,4);35秒到了(5,0);48秒到了(0,6);
∵(0,6)之前经过的轴上坐标为(5,0),
∴第47秒后点所在位置的坐标是(1,6).
故选:D.
6.【解答】解:∵点P(a,b)到y轴的距离为2,
∴|a|=2,
∴a=±2.
故选:B.
7.【解答】解:∵A(m﹣1,m+4)在x轴上,
∴m+4=0,
解得:m=﹣4,
∴m﹣1=﹣5,
∴点A的坐标是:(﹣5,0).
故选:B.
8.【解答】解:分析图象可以发现,点P的运动每4次位置循环一次.每循环一次向右移动四个单位.
∴2019=4×504+3,
当第504循环结束时,点P位置在(2016,0),在此基础之上运动三次到(2019,2),
故选:C.
9.【解答】解:∵点P(a,b)在第四象限,
∴a>0,b<0,
故选:D.
10.【解答】解:由图形可得:笑脸盖住的点在第二象限,故笑脸盖住的点的坐标可能为(﹣6,3).
故选:B.
二.填空题(共5小题)
11.【解答】解:∵点P(x,y)在第三象限,且点P到x轴的距离为3,到y轴的距离为2,
∴x=﹣2,y=﹣3,
∴点P的坐标是(﹣2,﹣3).
故答案为:(﹣2,﹣3).
12.【解答】解:∵点M(x,y)在第三象限,
∴x<0,y<0,
∴xy>0.
故答案为:>.
13.【解答】解:∵A(m,n)在第二象限,
∴m<0,n>0,
则点B(n,m)在第四象限.
故答案为:四.
14.【解答】解:∵点A在第二象限,
∴点A的横坐标为负,纵坐标为正,
∵点A到x轴的距离是它到y轴距离的2倍,
∴点A的坐标可以为:(﹣2,4)(答案不唯一).
故答案为:(﹣2,4)(答案不唯一).
15.【解答】解:∵A(x1,y1)在第二象限,
∴x1<0,y1>0,
∵B(x2,y2)在第三象限,
∴x2<0,y2<0,
∴x1y2>0,x2y1<0,
∴A
B=(x1y2,x2y1)在第四象限.
故答案为:四.
三.解答题(共4小题)
16.【解答】解:∵点P(2x﹣6,3x+1)在y轴上,
∴2x﹣6=0,
解得x=3,
所以,3x+1=9+1=10,
故P(0,10).
17.【解答】解:(1)∵xy=0,
∴x=0或y=0或x=0且y=0,
∴点M在y轴或x轴或原点;
(2)∵>0,
∴横纵坐标同号,
∴点M在第一象限或第三象限.
18.【解答】解:(1)要使点M在x轴上,a应满足2a+7=0,解得a=,
所以,当a=时,点M在x轴上;
(2)要使点M在第二象限,a应满足,解得,
所以,当时,点M在第二象限;
(3)要使点M到y轴距离是1,a应满足|a﹣1|=1,解得a=2或a=0,
所以,当a=2或a=0时,点M到y轴距离是1.
19.【解答】解:(1)点A(5,3)为“开心点”,理由如下,
当A(5,3)时,m﹣1=5,,得m=6,n=4,
则2m=12,8+n=12,
所以2m=8+n,
所以A(5,3)是“开心点”;
点B(4,10)不是“开心点”,理由如下,
当B(4,10)时,m﹣1=4,,得m=5,n=18,
则2m=10,8+18=26,
所以2m≠8+n,
所以点B(4,10)不是“开心点”;
(2)点M在第三象限,
理由如下:
∵点M(a,2a﹣1)是“开心点”,
∴m﹣1=a,,
∴m=a+1,n=4a﹣4,
代入2m=8+n有2a+2=8+4a﹣4,
∴a=﹣1,2a﹣1=﹣3,
∴M(﹣1,﹣3),
故点M在第三象限.
一.选择题
1.下列各点中,在第一象限的点是( )
A.(2,3)
B.(2,﹣1)
C.(﹣2,6)
D.(﹣1,﹣5)
2.若实数a,b满足关系式a﹣b2=1和a+b2=3,则点(a,b)有( )
A.1个
B.2个
C.3个
D.4个
3.点P(a,b)在第三象限,则点P到y轴的距离是( )
A.a
B.b
C.|a|
D.|b|
4.若点A(x,y)是第二象限内的点,则下列不等式中一定成立的是( )
A.x>y
B.x+y<0
C.xy>0
D.x﹣y<0
5.一个点在第一象限及x轴正半轴、y轴正半轴上运动,在第一秒钟,它从原点运动到(0,1),然后接着按图中箭头所示方向运动:(0,0)→(0,1)→(1,1)→(1,0)→……,且每秒移动一个单位,那么第47秒时,这个点所在位置的坐标是( )
A.(1,7)
B.(7,1)
C.(6,1)
D.(1,6)
6.若点P(a,b)到y轴的距离为2,则( )
A.a=2
B.a=±2
C.b=2
D.b=±2.
7.已知点A(m﹣1,m+4)在x轴上,则点A的坐标是( )
A.(0,5)
B.(﹣5,0)
C.(0,3)
D.(﹣3,0)
8.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),按这样的运动规律,经过第2019次运动后,动点P的坐标是( )
A.(2019,0)
B.(2019,1)
C.(2019,2)
D.(2020,0)
9.若点P(a,b)在第四象限,则( )
A.a>0,b>0
B.a<0,b<0
C.a<0,b>0
D.a>0,b<0
10.如图,笑脸盖住的点的坐标可能为( )
A.(5,2)
B.(﹣6,3)
C.(﹣4,﹣6)
D.(3,﹣4)
二.填空题
11.已知点P在第三象限,且点P到x轴的距离为3,到y轴的距离为2,那么点P的坐标为
.
12.如果点M(x,y)在第三象限,则xy的值
0.在第二象限,则点B(n,m)在第
象限.
14.点A在第二象限,它到x轴的距离是它到y轴距离的2倍,请写出一个满足条件的点A的坐标
.
15.对于平面坐标系中任意两点A(x1,y1),B(x2,y2)定义一种新运算“
”为:(x1,y1)
(x2,y2)=(x1y2,x2y1).若A(x1,y1)在第二象限,B(x2,y2)在第三象限,则A
B在第
象限.
三.解答题
16.已知点P(2x﹣6,3x+1)在y轴上,求P的坐标.
17.已知平面内点M(x,y),若x,y满足下列条件,请说出点M的位置.
(1)xy=0;
(2)>0.
18.平面直角坐标系中,有一点M(a﹣1,2a+7),试求满足下列条件的a的值.
(1)点M在x轴上;
(2)点M在第二象限;
(3)点M到y轴距离是1.
19.已知当m,n都是实数.且满足2m=8+n时,称p(m﹣1,)为“开心点”.
(1)判断点A(5,3),B(4,10)是否为“开心点”,并说明理由;
(2)若点M(a,2a﹣1)是“开心点”,请判断点M在第几象限?并说明理由.
参考答案与试题解析
一.选择题
1.【解答】解:A、(2,3),在第一象限,符合题意;
B、(2,﹣1)在第四象限,不合题意;
C、(﹣2,6)在第二象限,不合题意;
D、(﹣1,﹣5)在第三象限,不合题意.
故选:A.
2.【解答】解:∵a﹣b2=1和a+b2=3,
∴2a=4,
解得:a=2,
∴2﹣b2=1,
解得:b=±1,
∴点(a,b)有(2,1),(﹣2,1)共2个.
故选:B.
3.【解答】解:∵点P(a,b)在第三象限,
∴点P到y轴的距离是:|a|.
故选:C.
4.【解答】解:因为点A(x,y)是第二象限内的点,
所以x<0,y>0,
可得:x﹣y<0,x<y,xy<0,
故选:D.
5.【解答】解:这个点3秒时到了(1,0);8秒时到了(0,2);15秒时到了(3,0);24秒到了(0,4);35秒到了(5,0);48秒到了(0,6);
∵(0,6)之前经过的轴上坐标为(5,0),
∴第47秒后点所在位置的坐标是(1,6).
故选:D.
6.【解答】解:∵点P(a,b)到y轴的距离为2,
∴|a|=2,
∴a=±2.
故选:B.
7.【解答】解:∵A(m﹣1,m+4)在x轴上,
∴m+4=0,
解得:m=﹣4,
∴m﹣1=﹣5,
∴点A的坐标是:(﹣5,0).
故选:B.
8.【解答】解:分析图象可以发现,点P的运动每4次位置循环一次.每循环一次向右移动四个单位.
∴2019=4×504+3,
当第504循环结束时,点P位置在(2016,0),在此基础之上运动三次到(2019,2),
故选:C.
9.【解答】解:∵点P(a,b)在第四象限,
∴a>0,b<0,
故选:D.
10.【解答】解:由图形可得:笑脸盖住的点在第二象限,故笑脸盖住的点的坐标可能为(﹣6,3).
故选:B.
二.填空题(共5小题)
11.【解答】解:∵点P(x,y)在第三象限,且点P到x轴的距离为3,到y轴的距离为2,
∴x=﹣2,y=﹣3,
∴点P的坐标是(﹣2,﹣3).
故答案为:(﹣2,﹣3).
12.【解答】解:∵点M(x,y)在第三象限,
∴x<0,y<0,
∴xy>0.
故答案为:>.
13.【解答】解:∵A(m,n)在第二象限,
∴m<0,n>0,
则点B(n,m)在第四象限.
故答案为:四.
14.【解答】解:∵点A在第二象限,
∴点A的横坐标为负,纵坐标为正,
∵点A到x轴的距离是它到y轴距离的2倍,
∴点A的坐标可以为:(﹣2,4)(答案不唯一).
故答案为:(﹣2,4)(答案不唯一).
15.【解答】解:∵A(x1,y1)在第二象限,
∴x1<0,y1>0,
∵B(x2,y2)在第三象限,
∴x2<0,y2<0,
∴x1y2>0,x2y1<0,
∴A
B=(x1y2,x2y1)在第四象限.
故答案为:四.
三.解答题(共4小题)
16.【解答】解:∵点P(2x﹣6,3x+1)在y轴上,
∴2x﹣6=0,
解得x=3,
所以,3x+1=9+1=10,
故P(0,10).
17.【解答】解:(1)∵xy=0,
∴x=0或y=0或x=0且y=0,
∴点M在y轴或x轴或原点;
(2)∵>0,
∴横纵坐标同号,
∴点M在第一象限或第三象限.
18.【解答】解:(1)要使点M在x轴上,a应满足2a+7=0,解得a=,
所以,当a=时,点M在x轴上;
(2)要使点M在第二象限,a应满足,解得,
所以,当时,点M在第二象限;
(3)要使点M到y轴距离是1,a应满足|a﹣1|=1,解得a=2或a=0,
所以,当a=2或a=0时,点M到y轴距离是1.
19.【解答】解:(1)点A(5,3)为“开心点”,理由如下,
当A(5,3)时,m﹣1=5,,得m=6,n=4,
则2m=12,8+n=12,
所以2m=8+n,
所以A(5,3)是“开心点”;
点B(4,10)不是“开心点”,理由如下,
当B(4,10)时,m﹣1=4,,得m=5,n=18,
则2m=10,8+18=26,
所以2m≠8+n,
所以点B(4,10)不是“开心点”;
(2)点M在第三象限,
理由如下:
∵点M(a,2a﹣1)是“开心点”,
∴m﹣1=a,,
∴m=a+1,n=4a﹣4,
代入2m=8+n有2a+2=8+4a﹣4,
∴a=﹣1,2a﹣1=﹣3,
∴M(﹣1,﹣3),
故点M在第三象限.
