2.2.1综合法和分析法
图片预览





文档简介
(共18张PPT)
2.2.1 综合法和分析法
2.2直接证明与间接证明
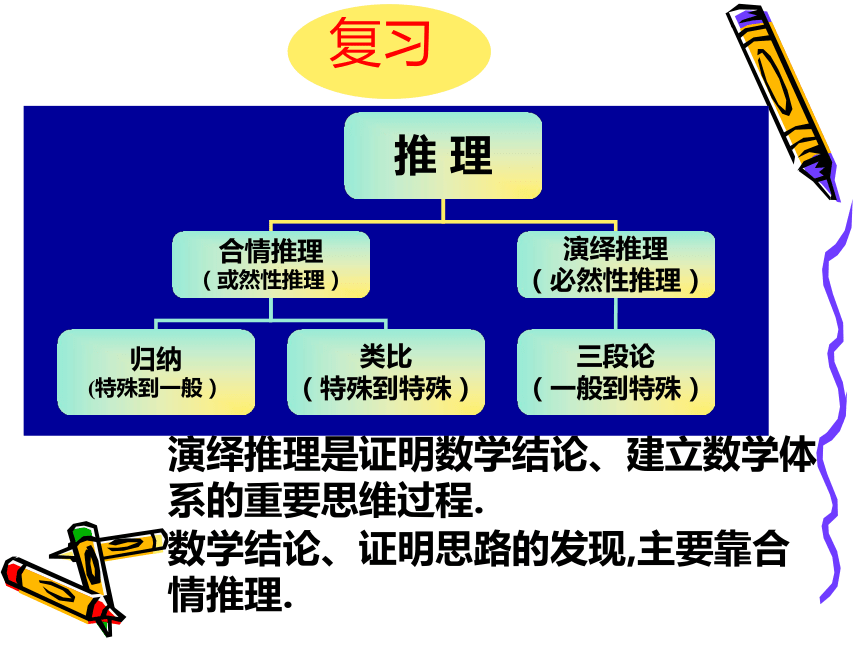
演绎推理是证明数学结论、建立数学体系的重要思维过程.
数学结论、证明思路的发现,主要靠合情推理.
复习
推 理
合情推理
(或然性推理)
演绎推理
(必然性推理)
归纳
(特殊到一般)
类比
(特殊到特殊)
三段论
(一般到特殊)
例1:已知a>0,b>0,求证a(b2+c2)+b(c2+a2)≥4abc
因为b2+c2 ≥2bc,a>0
所以a(b2+c2)≥2abc.
又因为c2+b2 ≥2bc,b>0
所以b(c2+a2)≥ 2abc.
因此a(b2+c2)+b(c2+a2)≥4abc.
证明:
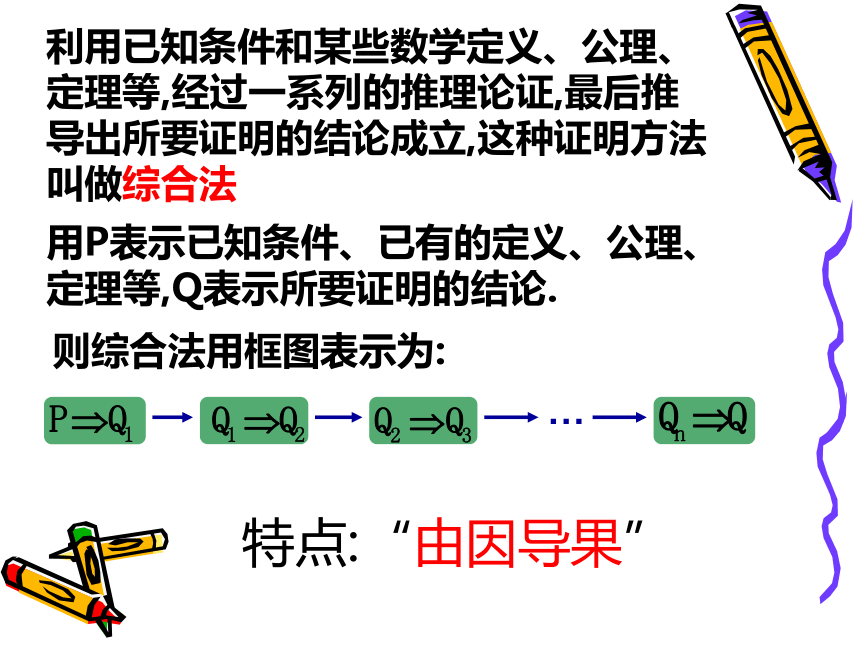
利用已知条件和某些数学定义、公理、定理等,经过一系列的推理论证,最后推导出所要证明的结论成立,这种证明方法叫做综合法
用P表示已知条件、已有的定义、公理、定理等,Q表示所要证明的结论.
则综合法用框图表示为:
…
特点:“由因导果”
例2:在△ABC中,三个内角A、B、C对应的边分别为a、b、c,且A、B、C成等差数列,a、b、c成等比数列,求证△ABC为等边三角形.
例3:在锐角三角形ABC中,
求证sinA+sinB+sinC>cosA+cosB+cosC
回顾基本不等式:
(a>0,b>0)的证明.
证明:
因为;
所以
所以
所以 成立
证明:要证;
只需证;
只需证;
只需证;
因为; 成立
所以 成立
一般地,从要证明的结论出发,逐步寻求推证过程中,使每一步结论成立的充分条件,直至最后,把要证明的结论归结为判定一个明显成立的条件(已知条件、定理、定义、公理等)为止,这种证明的方法叫做分析法.
特点:执果索因.
用框图表示分析法的思考过程、特点.
得到一个明显成立的结论
…
例4:如图,SA⊥平面ABC,AB⊥BC,过A作SB的垂线,垂足为E,过E作SC的垂线,垂足为F,求证 AF⊥SC
F
E
S
C
B
A
证明:要证AF⊥SC
只需证:SC⊥平面AEF
只需证:AE⊥SC
只需证:AE⊥平面SBC
只需证:AE⊥BC
只需证:BC⊥平面SAB
只需证:BC⊥SA
只需证:SA⊥平面ABC
因为:SA⊥平面ABC成立
所以. AF⊥SC成立
分析法.
特点:执果索因.
特点:“由因导果”
综合法
例5.设a , b , c三数成等比数列, 而x , y分别为a , b和b , c的等差中项, 求证: .
练习:已知a , b∈R+, 求证:
例6.设x , y∈R 且x2-2xy+2y2=2 , 求证: |x+y|<10 .
例7:已知数列{an}的通项an>0,(n∈N*),它的前n项的和记为sn,数列{s2n}是首项为3,公差为1的等差数列. (1)求an与sn的解析式; (2)试比较sn与3nan(n∈N*),的大小.
思考题:甲、乙、丙三箱共有小球384个,先由甲箱取出若干放进乙、丙两箱内,所放个数分别为乙、丙箱内原有个数,继而由乙箱取出若干个球放进甲、丙两箱内,最后由丙箱取出若干个球放进甲、乙两箱内,方法同前.结果三箱内的小球数恰好相等.求甲、乙、丙三箱原有小球数
甲:208个,乙:112个,丙:64个
证:
得到一个明显成立的结论
…
也可以是经过证明的结论
备用题
课堂小结
作业
2.2.1 综合法和分析法
2.2直接证明与间接证明
演绎推理是证明数学结论、建立数学体系的重要思维过程.
数学结论、证明思路的发现,主要靠合情推理.
复习
推 理
合情推理
(或然性推理)
演绎推理
(必然性推理)
归纳
(特殊到一般)
类比
(特殊到特殊)
三段论
(一般到特殊)
例1:已知a>0,b>0,求证a(b2+c2)+b(c2+a2)≥4abc
因为b2+c2 ≥2bc,a>0
所以a(b2+c2)≥2abc.
又因为c2+b2 ≥2bc,b>0
所以b(c2+a2)≥ 2abc.
因此a(b2+c2)+b(c2+a2)≥4abc.
证明:
利用已知条件和某些数学定义、公理、定理等,经过一系列的推理论证,最后推导出所要证明的结论成立,这种证明方法叫做综合法
用P表示已知条件、已有的定义、公理、定理等,Q表示所要证明的结论.
则综合法用框图表示为:
…
特点:“由因导果”
例2:在△ABC中,三个内角A、B、C对应的边分别为a、b、c,且A、B、C成等差数列,a、b、c成等比数列,求证△ABC为等边三角形.
例3:在锐角三角形ABC中,
求证sinA+sinB+sinC>cosA+cosB+cosC
回顾基本不等式:
(a>0,b>0)的证明.
证明:
因为;
所以
所以
所以 成立
证明:要证;
只需证;
只需证;
只需证;
因为; 成立
所以 成立
一般地,从要证明的结论出发,逐步寻求推证过程中,使每一步结论成立的充分条件,直至最后,把要证明的结论归结为判定一个明显成立的条件(已知条件、定理、定义、公理等)为止,这种证明的方法叫做分析法.
特点:执果索因.
用框图表示分析法的思考过程、特点.
得到一个明显成立的结论
…
例4:如图,SA⊥平面ABC,AB⊥BC,过A作SB的垂线,垂足为E,过E作SC的垂线,垂足为F,求证 AF⊥SC
F
E
S
C
B
A
证明:要证AF⊥SC
只需证:SC⊥平面AEF
只需证:AE⊥SC
只需证:AE⊥平面SBC
只需证:AE⊥BC
只需证:BC⊥平面SAB
只需证:BC⊥SA
只需证:SA⊥平面ABC
因为:SA⊥平面ABC成立
所以. AF⊥SC成立
分析法.
特点:执果索因.
特点:“由因导果”
综合法
例5.设a , b , c三数成等比数列, 而x , y分别为a , b和b , c的等差中项, 求证: .
练习:已知a , b∈R+, 求证:
例6.设x , y∈R 且x2-2xy+2y2=2 , 求证: |x+y|<10 .
例7:已知数列{an}的通项an>0,(n∈N*),它的前n项的和记为sn,数列{s2n}是首项为3,公差为1的等差数列. (1)求an与sn的解析式; (2)试比较sn与3nan(n∈N*),的大小.
思考题:甲、乙、丙三箱共有小球384个,先由甲箱取出若干放进乙、丙两箱内,所放个数分别为乙、丙箱内原有个数,继而由乙箱取出若干个球放进甲、丙两箱内,最后由丙箱取出若干个球放进甲、乙两箱内,方法同前.结果三箱内的小球数恰好相等.求甲、乙、丙三箱原有小球数
甲:208个,乙:112个,丙:64个
证:
得到一个明显成立的结论
…
也可以是经过证明的结论
备用题
课堂小结
作业
