北师大版七年级数学下第二章 相交线与平行线 章末 练习卷(word版含答案)
文档属性
| 名称 | 北师大版七年级数学下第二章 相交线与平行线 章末 练习卷(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 255.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-18 07:32:33 | ||
图片预览




文档简介
北师大版七年级数学下第二章 相交线与平行线章末练习卷
时间:90分钟 分值:100分
一、选择题(每小题3分,共30分)
1.下列四个角中,有可能与70°角互补的是
( )
2.在我们常见的英文字母中,存在着同位角、内错角、同旁内角的现象.在下列几个字母中,不含同旁内角现象的是
( )
A.E
B.F
C.N
D.H
3.如图所示,点A到BC所在的直线的距离是指图中线段 的长度
( )?
A.AC
B.AF
C.BD
D.CE
4.如图,直线AB,CD相交于点O,EO⊥AB于点O,若∠COE=55°,则∠BOD的度数为
( )
A.35°
B.45°
C.55°
D.25°
5.如图,直线a,b都与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠8=180°.其中能判定a∥b的条件是
( )
A.①②
B.②④
C.①③④
D.①②③④
6.如图,将一块三角尺的直角顶点放在直尺的一边上,当∠1=35°时,∠2的度数为
( )
A.35°
B.45°
C.55°
D.65°
7.如图,将一条两边沿互相平行的纸带折叠,已知α=76°,则∠1的度数为
( )
A.28°
B.30°
C.38°
D.45°
8.某同学在研究传统文化“抖空竹”时有一个发现:他把它抽象成数学问题,如图所示,已知AB∥CD,∠BAE=87°,∠DCE=121°,则∠E的度数是
( )
A.28°
B.34°
C.46°
D.56°
9.如图,已知AB∥CD,则α,β和γ之间的关系为
( )
A.β+γ-α=180°
B.α+γ=β
C.α+β+γ=360°
D.α+β-2γ=180°
10.在同一平面内,若∠A与∠B的两边分别垂直,且∠A比∠B的3倍少40°,则∠A的度数为
( )
A.20°
B.55°
C.20°或125°
D.20°或55°
二、填空题(每小题3分,共15分)
11.图是对顶角量角器,用它测量角的原理是 .?
12.已知a,b,c是直线,且a∥b,b∥c,则 ,理由是 .?
13.如图,A,B之间是一座山,一条铁路要通过A,B两地,现在A地测得铁路走向是北偏东71°,若A,B两地同时开工,要能使铁路在山中准确接通,则在B地施工应按南偏西 °.?
14.如图,AB∥EF∥CD,∠ABC=46°,∠BCE=20°,则∠CEF= °.?
15.如图,AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=α.则下列结论:①∠BOE=(180°-α);②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确的结论是 _________(填编号).?
三、解答题(共55分)
16.(6分)一个角的补角比它的余角的2倍多8°,求这个角的度数.
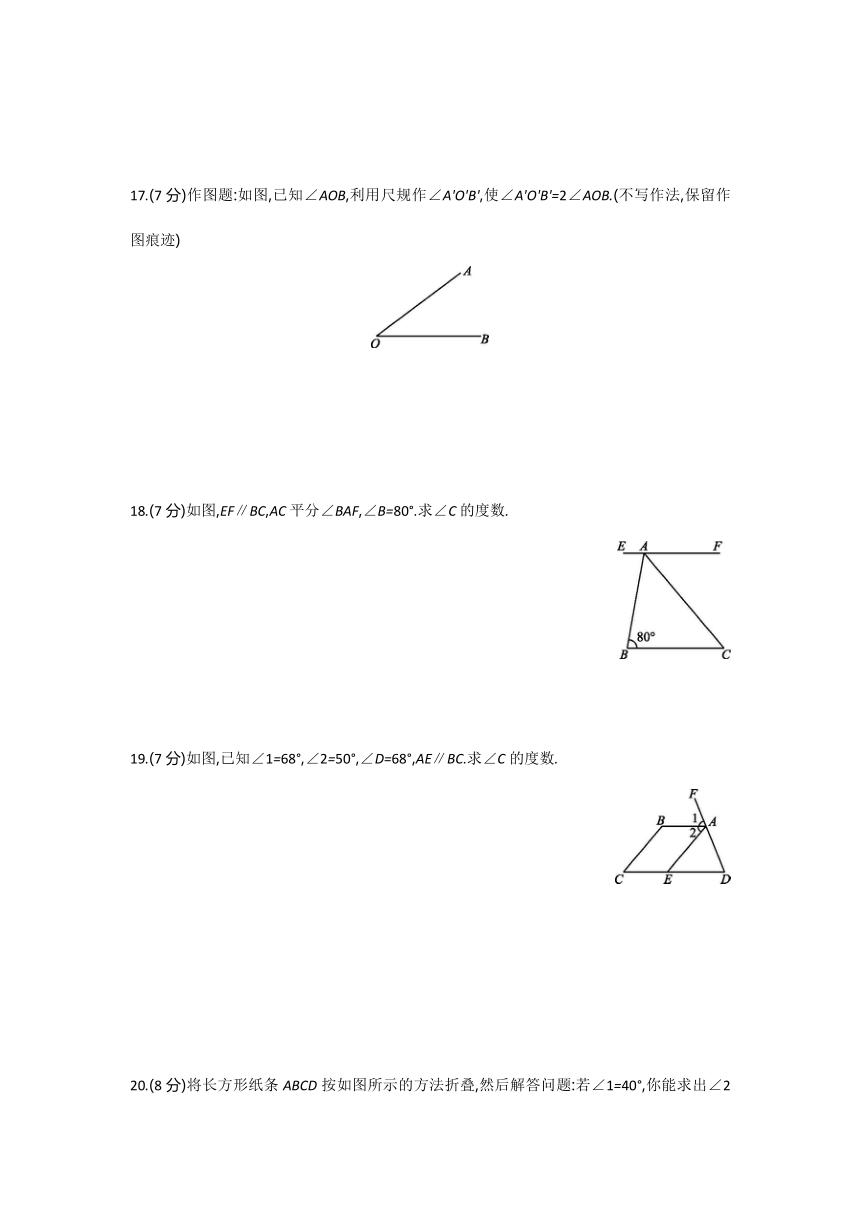
17.(7分)作图题:如图,已知∠AOB,利用尺规作∠A'O'B',使∠A'O'B'=2∠AOB.(不写作法,保留作图痕迹)
18.(7分)如图,EF∥BC,AC平分∠BAF,∠B=80°.求∠C的度数.
19.(7分)如图,已知∠1=68°,∠2=50°,∠D=68°,AE∥BC.求∠C的度数.
20.(8分)将长方形纸条ABCD按如图所示的方法折叠,然后解答问题:若∠1=40°,你能求出∠2的度数吗?试着做一做.
21.(8分)木工师傅为了充分利用材料,准备把两块等宽的长方形木板锯成图①和图②的形状,把它们拼接成一块较长的无缝的长方形木板使用,他量得∠1=138°,∠2=82°,那么他应把∠4和∠5分别锯成多大的角才能拼接成一块无缝的长方形木板?为什么?
22.(12分)已知AM∥CN,B为平面内一点,AB⊥BC于点B.
(1)如图①,直接写出∠A和∠C之间的数量关系: ;?
(2)如图②,过点B作BD⊥AM交AM的反向延长线于点D,∠ABD与∠C有何数量关系?说明理由;
(3)如图③,在(2)的条件下,点E,F在DM上,连接BE,BF,CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=5∠DBE,求∠EBC的度数.
参考答案
1.D 2.C 3.B 4.A 5.D
6.C 7.A 8.B 9.A 10.C
11.对顶角相等
12.a∥c 平行于同一条直线的两条直线平行
13.71 14.154
15.①②③ 解析:
①因为AB∥CD,
所以∠BOD=∠ABO=α,所以∠BOC=180°-α.又因为OE平分∠BOC,
所以∠BOE=∠EOC=∠BOC=(180°-α).
故①正确;
②因为OF⊥OE,所以∠EOF=90°,
所以∠BOF=90°-(180°-α)=α,
所以∠BOF=∠BOD,
所以OF平分∠BOD.
故②正确;
③因为OP⊥CD,所以∠COP=∠DOP=90°,
所以∠POE=90°-∠EOC=α,
所以∠POE=∠BOF.
故③正确;
所以∠POB=90°-α,
而∠DOF=α,所以④错误.
16.解:设这个角的度数为x°,则这个角的余角为(90-x)°,补角为(180-x)°.
由题意,得180-x=2(90-x)+8,
解得x=8.
故这个角的度数是8°.
17.解:如图,∠A'O'B'即为所求.
18.解:因为EF∥BC,
所以∠BAF=180°-∠B=100°.
因为AC平分∠BAF,
所以∠CAF=∠BAF=50°.
因为EF∥BC,
所以∠C=∠CAF=50°.
19.解:因为∠1=∠D=68°,
所以AB∥CD,
所以∠AED=∠2=50°.
因为AE∥BC,
所以∠C=∠AED=50°.
20.解:因为AP∥BF,
所以∠CFB=∠1=40°.
因为∠CFB+2∠CFE=180°,
所以∠CFE=70°.
因为AE∥BF,
所以∠2+∠BFE=180°,
所以∠2=180°-∠CFE-∠CFB=180°-70°-40°=70°.
21.解:∠4=42°,∠5=40°.
理由:如图,过点F作EF∥AB,
则∠1+∠BFE=180°.
因为∠1=138°,
所以∠BFE=42°.
因为∠2=82°,
所以∠DFE=40°.
因为EF∥AB,AB∥CD,
所以EF∥CD,
所以∠3+∠DFE=180°,
所以∠3=180°-∠DFE=140°.
因为把两块木板拼成一块无缝的长方形木板,
所以∠1+∠4=180°,∠5+∠3=180°,
所以∠4=180°-∠1=42°,∠5=180°-∠3=40°.
22.解:(1)如图①,设AM与BC的交点为O.
因为AM∥CN,
所以∠C=∠AOB.
因为AB⊥BC,
所以∠B=90°,
所以∠A+∠AOB=180°-90°=90°,
所以∠A+∠C=90°.
故答案为∠A+∠C=90°.
(2)∠ABD=∠C.理由:如图②,过点B作BG∥DM,则∠ADB+∠DBG=180°.
因为BD⊥AM,所以∠ADB=90°,
所以∠DBG=90°,
即∠ABD+∠ABG=90°.
因为AB⊥BC,
所以∠CBG+∠ABG=90°,
所以∠ABD=∠CBG.
因为AM∥CN,BG∥AM,
所以CN∥BG,
所以∠C=∠CBG,
所以∠ABD=∠C.
(3)如图③,过点B作BG∥DM.
因为BF平分∠DBC,BE平分∠ABD,
所以∠DBF=∠CBF,∠DBE=∠ABE.
由(2)可得∠ABD=∠CBG,
所以∠ABF=∠GBF.
设∠DBE=α,则∠ABE=α,∠ABD=2α=∠CBG=∠BCN,∠BFC=5∠DBE=5α.
因为AB⊥BC,所以∠ABC=90°,
所以∠ABG=∠ABC-∠CBG=90°-2α,
所以∠ABF=∠GBF=45°-α,
所以∠CBF=45°-α+2α=45°+α.
因为AM∥CN,所以∠AFC+∠NCF=180°.
因为∠FCB+∠NCF=180°,
所以∠FCB=∠AFC==90°-α.
在三角形BCF中,由∠BFC+∠CBF+∠FCB=180°,
可得5α+45°+α+90°-α=180°,解得α=9°,
所以∠ABE=9°,
所以∠EBC=∠ABE+∠ABC=9°+90°=99°.
时间:90分钟 分值:100分
一、选择题(每小题3分,共30分)
1.下列四个角中,有可能与70°角互补的是
( )
2.在我们常见的英文字母中,存在着同位角、内错角、同旁内角的现象.在下列几个字母中,不含同旁内角现象的是
( )
A.E
B.F
C.N
D.H
3.如图所示,点A到BC所在的直线的距离是指图中线段 的长度
( )?
A.AC
B.AF
C.BD
D.CE
4.如图,直线AB,CD相交于点O,EO⊥AB于点O,若∠COE=55°,则∠BOD的度数为
( )
A.35°
B.45°
C.55°
D.25°
5.如图,直线a,b都与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠8=180°.其中能判定a∥b的条件是
( )
A.①②
B.②④
C.①③④
D.①②③④
6.如图,将一块三角尺的直角顶点放在直尺的一边上,当∠1=35°时,∠2的度数为
( )
A.35°
B.45°
C.55°
D.65°
7.如图,将一条两边沿互相平行的纸带折叠,已知α=76°,则∠1的度数为
( )
A.28°
B.30°
C.38°
D.45°
8.某同学在研究传统文化“抖空竹”时有一个发现:他把它抽象成数学问题,如图所示,已知AB∥CD,∠BAE=87°,∠DCE=121°,则∠E的度数是
( )
A.28°
B.34°
C.46°
D.56°
9.如图,已知AB∥CD,则α,β和γ之间的关系为
( )
A.β+γ-α=180°
B.α+γ=β
C.α+β+γ=360°
D.α+β-2γ=180°
10.在同一平面内,若∠A与∠B的两边分别垂直,且∠A比∠B的3倍少40°,则∠A的度数为
( )
A.20°
B.55°
C.20°或125°
D.20°或55°
二、填空题(每小题3分,共15分)
11.图是对顶角量角器,用它测量角的原理是 .?
12.已知a,b,c是直线,且a∥b,b∥c,则 ,理由是 .?
13.如图,A,B之间是一座山,一条铁路要通过A,B两地,现在A地测得铁路走向是北偏东71°,若A,B两地同时开工,要能使铁路在山中准确接通,则在B地施工应按南偏西 °.?
14.如图,AB∥EF∥CD,∠ABC=46°,∠BCE=20°,则∠CEF= °.?
15.如图,AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=α.则下列结论:①∠BOE=(180°-α);②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确的结论是 _________(填编号).?
三、解答题(共55分)
16.(6分)一个角的补角比它的余角的2倍多8°,求这个角的度数.
17.(7分)作图题:如图,已知∠AOB,利用尺规作∠A'O'B',使∠A'O'B'=2∠AOB.(不写作法,保留作图痕迹)
18.(7分)如图,EF∥BC,AC平分∠BAF,∠B=80°.求∠C的度数.
19.(7分)如图,已知∠1=68°,∠2=50°,∠D=68°,AE∥BC.求∠C的度数.
20.(8分)将长方形纸条ABCD按如图所示的方法折叠,然后解答问题:若∠1=40°,你能求出∠2的度数吗?试着做一做.
21.(8分)木工师傅为了充分利用材料,准备把两块等宽的长方形木板锯成图①和图②的形状,把它们拼接成一块较长的无缝的长方形木板使用,他量得∠1=138°,∠2=82°,那么他应把∠4和∠5分别锯成多大的角才能拼接成一块无缝的长方形木板?为什么?
22.(12分)已知AM∥CN,B为平面内一点,AB⊥BC于点B.
(1)如图①,直接写出∠A和∠C之间的数量关系: ;?
(2)如图②,过点B作BD⊥AM交AM的反向延长线于点D,∠ABD与∠C有何数量关系?说明理由;
(3)如图③,在(2)的条件下,点E,F在DM上,连接BE,BF,CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=5∠DBE,求∠EBC的度数.
参考答案
1.D 2.C 3.B 4.A 5.D
6.C 7.A 8.B 9.A 10.C
11.对顶角相等
12.a∥c 平行于同一条直线的两条直线平行
13.71 14.154
15.①②③ 解析:
①因为AB∥CD,
所以∠BOD=∠ABO=α,所以∠BOC=180°-α.又因为OE平分∠BOC,
所以∠BOE=∠EOC=∠BOC=(180°-α).
故①正确;
②因为OF⊥OE,所以∠EOF=90°,
所以∠BOF=90°-(180°-α)=α,
所以∠BOF=∠BOD,
所以OF平分∠BOD.
故②正确;
③因为OP⊥CD,所以∠COP=∠DOP=90°,
所以∠POE=90°-∠EOC=α,
所以∠POE=∠BOF.
故③正确;
所以∠POB=90°-α,
而∠DOF=α,所以④错误.
16.解:设这个角的度数为x°,则这个角的余角为(90-x)°,补角为(180-x)°.
由题意,得180-x=2(90-x)+8,
解得x=8.
故这个角的度数是8°.
17.解:如图,∠A'O'B'即为所求.
18.解:因为EF∥BC,
所以∠BAF=180°-∠B=100°.
因为AC平分∠BAF,
所以∠CAF=∠BAF=50°.
因为EF∥BC,
所以∠C=∠CAF=50°.
19.解:因为∠1=∠D=68°,
所以AB∥CD,
所以∠AED=∠2=50°.
因为AE∥BC,
所以∠C=∠AED=50°.
20.解:因为AP∥BF,
所以∠CFB=∠1=40°.
因为∠CFB+2∠CFE=180°,
所以∠CFE=70°.
因为AE∥BF,
所以∠2+∠BFE=180°,
所以∠2=180°-∠CFE-∠CFB=180°-70°-40°=70°.
21.解:∠4=42°,∠5=40°.
理由:如图,过点F作EF∥AB,
则∠1+∠BFE=180°.
因为∠1=138°,
所以∠BFE=42°.
因为∠2=82°,
所以∠DFE=40°.
因为EF∥AB,AB∥CD,
所以EF∥CD,
所以∠3+∠DFE=180°,
所以∠3=180°-∠DFE=140°.
因为把两块木板拼成一块无缝的长方形木板,
所以∠1+∠4=180°,∠5+∠3=180°,
所以∠4=180°-∠1=42°,∠5=180°-∠3=40°.
22.解:(1)如图①,设AM与BC的交点为O.
因为AM∥CN,
所以∠C=∠AOB.
因为AB⊥BC,
所以∠B=90°,
所以∠A+∠AOB=180°-90°=90°,
所以∠A+∠C=90°.
故答案为∠A+∠C=90°.
(2)∠ABD=∠C.理由:如图②,过点B作BG∥DM,则∠ADB+∠DBG=180°.
因为BD⊥AM,所以∠ADB=90°,
所以∠DBG=90°,
即∠ABD+∠ABG=90°.
因为AB⊥BC,
所以∠CBG+∠ABG=90°,
所以∠ABD=∠CBG.
因为AM∥CN,BG∥AM,
所以CN∥BG,
所以∠C=∠CBG,
所以∠ABD=∠C.
(3)如图③,过点B作BG∥DM.
因为BF平分∠DBC,BE平分∠ABD,
所以∠DBF=∠CBF,∠DBE=∠ABE.
由(2)可得∠ABD=∠CBG,
所以∠ABF=∠GBF.
设∠DBE=α,则∠ABE=α,∠ABD=2α=∠CBG=∠BCN,∠BFC=5∠DBE=5α.
因为AB⊥BC,所以∠ABC=90°,
所以∠ABG=∠ABC-∠CBG=90°-2α,
所以∠ABF=∠GBF=45°-α,
所以∠CBF=45°-α+2α=45°+α.
因为AM∥CN,所以∠AFC+∠NCF=180°.
因为∠FCB+∠NCF=180°,
所以∠FCB=∠AFC==90°-α.
在三角形BCF中,由∠BFC+∠CBF+∠FCB=180°,
可得5α+45°+α+90°-α=180°,解得α=9°,
所以∠ABE=9°,
所以∠EBC=∠ABE+∠ABC=9°+90°=99°.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
