北师大版数学九年级上册 第六章 反比例函数复习教案
文档属性
| 名称 | 北师大版数学九年级上册 第六章 反比例函数复习教案 |  | |
| 格式 | zip | ||
| 文件大小 | 217.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-18 09:31:47 | ||
图片预览

文档简介
一、教学目标:
1.理解并会应用反比例函数的定义
2.体会函数的三种表示方法的互相转换.对函数进行认识上的整合.
3.逐步提高从函数图象中获取信息的能力,探索并掌握反比例函数的主要性质.
二、教学重点:
画反比例函数的图象;并从函数图象中获取信息,探索并研究反比例函数的主要性质.
三、教学难点:
反比例函数的图象特点及性质的探究.
四、教学过程
(一)知识点与例题演练
知识点一
1.什么叫反比例函数?
一般地,如果两个变量x,y之间的关系可以表示成:
(k为常数,k≠0)的形式,那么称y是x的反比例函数.自变量x不能为零.
2.反比例函数有哪些等价形式?
反比例函数的三种形式:
练习1:
1、函数
中,反比例函数有
个
2、已知,与x成反比例,与x-2成正比例,且当x
=
1时,y=-1;x=3时,y=5.求y与x的函数关系式.
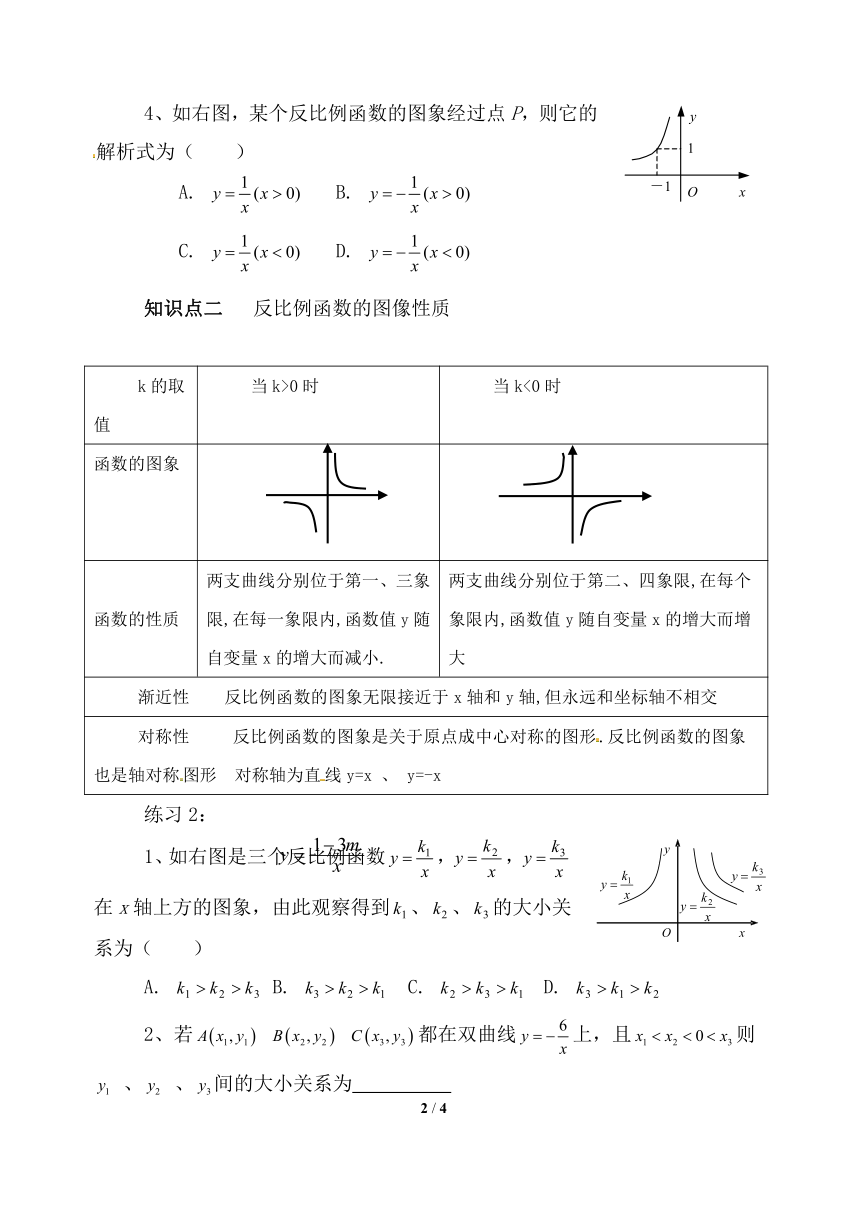
4、如右图,某个反比例函数的图象经过点P,则它的解析式为(
)
A.
B.
C.
D.
知识点二
反比例函数的图像性质
k的取值
当k>0时
当k<0时
函数的图象
函数的性质
两支曲线分别位于第一、三象限,在每一象限内,函数值y随自变量x的增大而减小.
两支曲线分别位于第二、四象限,在每个象限内,函数值y随自变量x的增大而增大
渐近性
反比例函数的图象无限接近于x轴和y轴,但永远和坐标轴不相交
对称性
反比例函数的图象是关于原点成中心对称的图形.反比例函数的图象也是轴对称图形
对称轴为直线y=x
、
y=-x
练习2:
1、如右图是三个反比例函数,,在x轴上方的图象,由此观察得到、、的大小关系为(
)
A.
B.
C.
D.
2、若
都在双曲线上,且则
、
、间的大小关系为
3、函数y=ax-a
与(a≠0)在同一直角坐标系中的图象可能是(
)
知识点三、与面积有关的问题:
面积性质(一):
设P(m,n)是双曲线(k≠0)上任意一点,过P作x轴的垂线,垂足为A,则
若将此题改为过P点作y轴的垂线段,其结论成立吗?
面积性质(二)
过P分别作x轴、y轴的垂线,垂足为A,B,则
练习3:
1、如图,点P是反比例函数
图象上的一点,PD⊥x轴于D.
则△POD的面积为
.
综合练习:
一次函数y=kx+b的图象与反比例函数
图象相交于A(-1,m),B(n,-1)两点.
(1)
写出这个一次函数的表达式;
(2)
画出函数图象草图,并据此写出使一次函
数值大于反比例函数值的x的取值范围.
(二)随堂练习,巩固深化
如右图,△OPQ是边长为2的等边三角形,若反比例函数的图象过点P,则它的解析式是_____________
2、某新建的大楼楼体外表需贴磁砖,楼体外表总面积为4000。
(1)设所需磁砖的块数为(块),每块磁砖的面积为(),试求与的函数关系式;(2)如果每块磁砖的面积均为80,每箱磁砖有120块,需买磁砖多少箱?
3、已知:如图,一次函数的图象与反比例函数的图象相交与A、B两点,且点A的横坐标和点B的纵坐标都是。
(1)求A、B两点的坐标(4分)
(2)求反例函数的解析式(2分)
(3)求的面积。(2分)
【作业布置】
本节讲义完成
6
/
6
1.理解并会应用反比例函数的定义
2.体会函数的三种表示方法的互相转换.对函数进行认识上的整合.
3.逐步提高从函数图象中获取信息的能力,探索并掌握反比例函数的主要性质.
二、教学重点:
画反比例函数的图象;并从函数图象中获取信息,探索并研究反比例函数的主要性质.
三、教学难点:
反比例函数的图象特点及性质的探究.
四、教学过程
(一)知识点与例题演练
知识点一
1.什么叫反比例函数?
一般地,如果两个变量x,y之间的关系可以表示成:
(k为常数,k≠0)的形式,那么称y是x的反比例函数.自变量x不能为零.
2.反比例函数有哪些等价形式?
反比例函数的三种形式:
练习1:
1、函数
中,反比例函数有
个
2、已知,与x成反比例,与x-2成正比例,且当x
=
1时,y=-1;x=3时,y=5.求y与x的函数关系式.
4、如右图,某个反比例函数的图象经过点P,则它的解析式为(
)
A.
B.
C.
D.
知识点二
反比例函数的图像性质
k的取值
当k>0时
当k<0时
函数的图象
函数的性质
两支曲线分别位于第一、三象限,在每一象限内,函数值y随自变量x的增大而减小.
两支曲线分别位于第二、四象限,在每个象限内,函数值y随自变量x的增大而增大
渐近性
反比例函数的图象无限接近于x轴和y轴,但永远和坐标轴不相交
对称性
反比例函数的图象是关于原点成中心对称的图形.反比例函数的图象也是轴对称图形
对称轴为直线y=x
、
y=-x
练习2:
1、如右图是三个反比例函数,,在x轴上方的图象,由此观察得到、、的大小关系为(
)
A.
B.
C.
D.
2、若
都在双曲线上,且则
、
、间的大小关系为
3、函数y=ax-a
与(a≠0)在同一直角坐标系中的图象可能是(
)
知识点三、与面积有关的问题:
面积性质(一):
设P(m,n)是双曲线(k≠0)上任意一点,过P作x轴的垂线,垂足为A,则
若将此题改为过P点作y轴的垂线段,其结论成立吗?
面积性质(二)
过P分别作x轴、y轴的垂线,垂足为A,B,则
练习3:
1、如图,点P是反比例函数
图象上的一点,PD⊥x轴于D.
则△POD的面积为
.
综合练习:
一次函数y=kx+b的图象与反比例函数
图象相交于A(-1,m),B(n,-1)两点.
(1)
写出这个一次函数的表达式;
(2)
画出函数图象草图,并据此写出使一次函
数值大于反比例函数值的x的取值范围.
(二)随堂练习,巩固深化
如右图,△OPQ是边长为2的等边三角形,若反比例函数的图象过点P,则它的解析式是_____________
2、某新建的大楼楼体外表需贴磁砖,楼体外表总面积为4000。
(1)设所需磁砖的块数为(块),每块磁砖的面积为(),试求与的函数关系式;(2)如果每块磁砖的面积均为80,每箱磁砖有120块,需买磁砖多少箱?
3、已知:如图,一次函数的图象与反比例函数的图象相交与A、B两点,且点A的横坐标和点B的纵坐标都是。
(1)求A、B两点的坐标(4分)
(2)求反例函数的解析式(2分)
(3)求的面积。(2分)
【作业布置】
本节讲义完成
6
/
6
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
