鲁教版(五四制)数学七年级数学上第三章勾股定理复习检测试卷(Word版含答案)
文档属性
| 名称 | 鲁教版(五四制)数学七年级数学上第三章勾股定理复习检测试卷(Word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 135.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-18 07:44:13 | ||
图片预览


文档简介
鲁教版数学七年级数学上第三章-一勾股定理
复习检测
一、选择题
下列已知三角形的三边长,其中为直角三角形的是
A.
2,4,6
B.
4,6,8
C.
6,8,10
D.
10,12,14
下列各组数:、4、5;?、5、6;?、15、17;、2、3,其中是勾股数的有
A.
4组
B.
3组
C.
2组
D.
1组
下列各组数据中,能作为直角三角形三边长的是
A.
2,3,4
B.
4,5,
C.
,,
D.
9,15,17
如图,一棵大树在离地面6米高的B处断裂,树顶A落在离树底部C的8米处,则大树断裂之前的高度为
A.
10米
B.
16米
C.
15米
D.
14米
已知一轮船以18海里小时的速度从港口A出发向西南方向航行,另一轮船以24海里小时的速度同时从港口A出发向东南方向航行,离开港口后,两轮船相距
A.
30海里
B.
35海里
C.
40海里
D.
45海里
如图,是一扇高为2m,宽为的门框,童师傅有3块薄木板,尺寸如下:号木板长3m,宽;号木板长,宽;号木板长4m,宽可以从这扇门通过的木板是号.
A.
B.
C.
D.
都不能通过
已知一个三角形的三边长分别为a、b、c,且它们满足,则该三角形的形状为
A.
锐角三角形
B.
直角三角形
C.
钝角三角形
D.
无法确定
已知一轮船以的速度从港口A出发向西南方向航行,另一轮船以的速度同时从港口A出发向东南方向航行,离开港口后,两轮船相距
A.
B.
C.
D.
如图所示,在长方形ABCD中,,,若将长方形ABCD沿DE折叠,使点C落在AB边上的点F处,则线段CE的长为?
?
?
?
A.
B.
C.
D.
10
如图,一个梯子AB斜靠在一竖直的墙AO上,测得若梯子的顶端沿墙下滑米,这时梯子的底端也恰好外移米,则梯子的长度AB为?
?
A.
B.
C.
D.
如图,王大伯家屋后有一块长12m、宽8m的长方形空地,他在以较长边BC为直径的半圆内种菜,他家养的一只羊平时拴在A处的一棵树上,为了不让羊吃到菜,拴羊的绳长最长不超过()
A.
3m
B.
4m
C.
5m
D.
6m
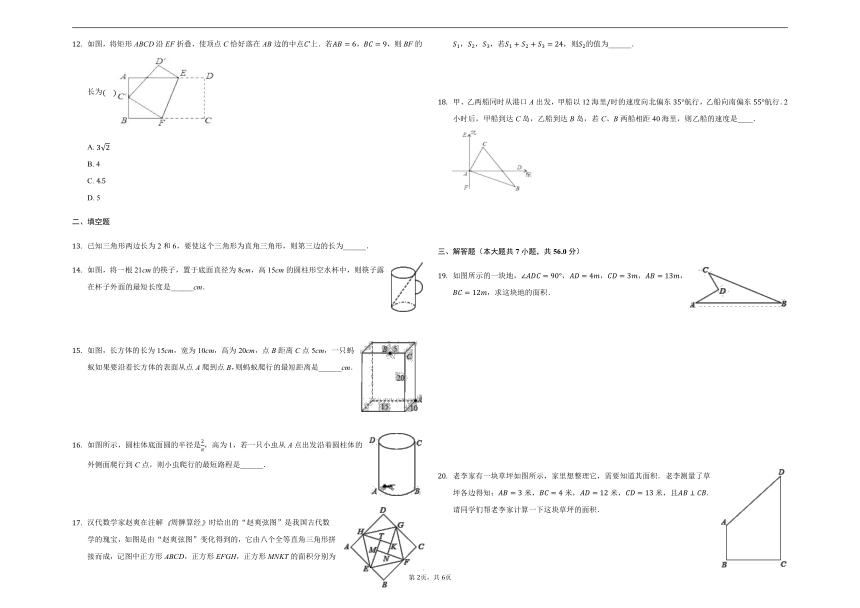
如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的中点上.若,,则BF的长为
A.
B.
4
C.
D.
5
二、填空题
已知三角形两边长为2和6,要使这个三角形为直角三角形,则第三边的长为______.
如图,将一根21cm的筷子,置于底面直径为8cm,高15cm的圆柱形空水杯中,则筷子露在杯子外面的最短长度是______cm.
如图,长方体的长为15cm,宽为10cm,高为20cm,点B距离C点5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,则蚂蚁爬行的最短距离是______cm.
如图所示,圆柱体底面圆的半径是,高为1,若一只小虫从A点出发沿着圆柱体的外侧面爬行到C点,则小虫爬行的最短路程是______.
汉代数学家赵爽在注解周髀算经时给出的“赵爽弦图”是我国古代数学的瑰宝,如图是由“赵爽弦图”变化得到的,它由八个全等直角三角形拼接而成,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为,,,若,则的值为______.
甲、乙两船同时从港口A出发,甲船以12海里时的速度向北偏东航行,乙船向南偏东航行.2小时后,甲船到达C岛,乙船到达B岛,若C、B两船相距40海里,则乙船的速度是____.
三、解答题(本大题共7小题,共56.0分)
如图所示的一块地,,,,,,求这块地的面积.
老李家有一块草坪如图所示,家里想整理它,需要知道其面积.老李测量了草坪各边得知:米,米,米,米,且请同学们帮老李家计算一下这块草坪的面积.
为了积极响应国家新农村建设,遂宁市某镇政府采用了移动宣讲的形式进行宣传动员.如图,笔直公路MN的一侧点A处有一村庄,村庄A到公路MN的距离为600米,假使宣讲车P周围1000米以内能听到广播宣传,宣讲车P在公路MN上沿PN方向行驶时:
请问村庄能否听到宣传,请说明理由;
如果能听到,已知宣讲车的速度是200米分钟,那么村庄总共能听到多长时间的宣传?
如图,一架长25米的梯子,斜靠在竖直的墙上,这时梯子底端离墙7米.
此时梯子顶端离地面多少米?
若梯子顶端下滑4米,那么梯子底端将向左滑动多少米?
在杭州西湖风景游船处,如图,在离水面高度为5m的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为13m,此人以的速度收绳后船移动到点D的位置,问船向岸边移动了多少m?假设绳子是直的,结果保留根号
如图,把一块三角形土地挖去一个直角三角形后,测得米,米,米,米.求剩余土地图中阴影部分的面积.
扇形OAB是一个以O为圆心,半径为4千米且圆心角为的风景区,C是弧AB上的一个动点,CD、CE为风景区中的两条景观人行道,、,垂足分别为D,E,DE是风景区中的商业街,已知商业街每年能为风景区带来每千米200万元的经济效益,请问在C运动的过程中风景区商业街DE每年的经济效益是否为定值?如果是,求出该定值;如果不是,请说明理由.
答案
1.【答案】C
2.【答案】C
3.【答案】B
4.【答案】B
5.【答案】D
6.【答案】B
7.【答案】B
8.【答案】D
9.【答案】C
10.【答案】A
11.【答案】B
12.【答案】B
13.【答案】或
14.【答案】4
15.【答案】25
16.【答案】
17.【答案】8
18.【答案】16海里时
19.【答案】解:连接AC,
,,,
.
由,可得,
是直角三角形,
,,
故这块地的面积为.
20.【答案】解:连接AC,如图,
,
,
米,米,
米,
米,米,
,
为直角三角形,
这块草坪的面积米
21.【答案】解:村庄能否听到宣传,
理由:村庄A到公路MN的距离为600米米,
村庄能听到宣传;
如图:假设当宣讲车行驶到P点开始影响村庄,行驶QD点结束对村庄的影响,
则米,米,
米,
米,
影响村庄的时间为:分钟,
村庄总共能听到8分钟的宣传.
22.【答案】解:米,米,
梯子距离地面的高度米.
答:此时梯子顶端离地面24米;
梯子下滑了4米,即梯子距离地面的高度米,
,
米,即下端滑行了8米.
答:梯子底端将向左滑动了8米.
23.【答案】解:在中,,,,
,
此人以的速度收绳,10s后船移动到点D的位置,
,
,
.
答:船向岸边移动了.
24.【答案】解:在中,
米,米,米,米,
,
取正值.
在中,,.
,
为直角三角形,.
米
答:剩余土地图中阴影部分的面积为:96米.
25.【答案】解:结论:在C运动的过程中风景区商业街DE每年的经济效益是定值.
理由:如图,连接OC,交DE于J,取POC的中点K,连接DK,KE.
,,
,
,
,
,D,C,E四点共圆,
,
,
是定值,是定值,
弦DE的长是定值,
当点C是的中点时,千米,
此时,,
千米,
在C运动的过程中风景区商业街DE每年的经济效益是定值,
万元,
定值为万元.
第2页,共5页
第5页,共5页
复习检测
一、选择题
下列已知三角形的三边长,其中为直角三角形的是
A.
2,4,6
B.
4,6,8
C.
6,8,10
D.
10,12,14
下列各组数:、4、5;?、5、6;?、15、17;、2、3,其中是勾股数的有
A.
4组
B.
3组
C.
2组
D.
1组
下列各组数据中,能作为直角三角形三边长的是
A.
2,3,4
B.
4,5,
C.
,,
D.
9,15,17
如图,一棵大树在离地面6米高的B处断裂,树顶A落在离树底部C的8米处,则大树断裂之前的高度为
A.
10米
B.
16米
C.
15米
D.
14米
已知一轮船以18海里小时的速度从港口A出发向西南方向航行,另一轮船以24海里小时的速度同时从港口A出发向东南方向航行,离开港口后,两轮船相距
A.
30海里
B.
35海里
C.
40海里
D.
45海里
如图,是一扇高为2m,宽为的门框,童师傅有3块薄木板,尺寸如下:号木板长3m,宽;号木板长,宽;号木板长4m,宽可以从这扇门通过的木板是号.
A.
B.
C.
D.
都不能通过
已知一个三角形的三边长分别为a、b、c,且它们满足,则该三角形的形状为
A.
锐角三角形
B.
直角三角形
C.
钝角三角形
D.
无法确定
已知一轮船以的速度从港口A出发向西南方向航行,另一轮船以的速度同时从港口A出发向东南方向航行,离开港口后,两轮船相距
A.
B.
C.
D.
如图所示,在长方形ABCD中,,,若将长方形ABCD沿DE折叠,使点C落在AB边上的点F处,则线段CE的长为?
?
?
?
A.
B.
C.
D.
10
如图,一个梯子AB斜靠在一竖直的墙AO上,测得若梯子的顶端沿墙下滑米,这时梯子的底端也恰好外移米,则梯子的长度AB为?
?
A.
B.
C.
D.
如图,王大伯家屋后有一块长12m、宽8m的长方形空地,他在以较长边BC为直径的半圆内种菜,他家养的一只羊平时拴在A处的一棵树上,为了不让羊吃到菜,拴羊的绳长最长不超过()
A.
3m
B.
4m
C.
5m
D.
6m
如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的中点上.若,,则BF的长为
A.
B.
4
C.
D.
5
二、填空题
已知三角形两边长为2和6,要使这个三角形为直角三角形,则第三边的长为______.
如图,将一根21cm的筷子,置于底面直径为8cm,高15cm的圆柱形空水杯中,则筷子露在杯子外面的最短长度是______cm.
如图,长方体的长为15cm,宽为10cm,高为20cm,点B距离C点5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,则蚂蚁爬行的最短距离是______cm.
如图所示,圆柱体底面圆的半径是,高为1,若一只小虫从A点出发沿着圆柱体的外侧面爬行到C点,则小虫爬行的最短路程是______.
汉代数学家赵爽在注解周髀算经时给出的“赵爽弦图”是我国古代数学的瑰宝,如图是由“赵爽弦图”变化得到的,它由八个全等直角三角形拼接而成,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为,,,若,则的值为______.
甲、乙两船同时从港口A出发,甲船以12海里时的速度向北偏东航行,乙船向南偏东航行.2小时后,甲船到达C岛,乙船到达B岛,若C、B两船相距40海里,则乙船的速度是____.
三、解答题(本大题共7小题,共56.0分)
如图所示的一块地,,,,,,求这块地的面积.
老李家有一块草坪如图所示,家里想整理它,需要知道其面积.老李测量了草坪各边得知:米,米,米,米,且请同学们帮老李家计算一下这块草坪的面积.
为了积极响应国家新农村建设,遂宁市某镇政府采用了移动宣讲的形式进行宣传动员.如图,笔直公路MN的一侧点A处有一村庄,村庄A到公路MN的距离为600米,假使宣讲车P周围1000米以内能听到广播宣传,宣讲车P在公路MN上沿PN方向行驶时:
请问村庄能否听到宣传,请说明理由;
如果能听到,已知宣讲车的速度是200米分钟,那么村庄总共能听到多长时间的宣传?
如图,一架长25米的梯子,斜靠在竖直的墙上,这时梯子底端离墙7米.
此时梯子顶端离地面多少米?
若梯子顶端下滑4米,那么梯子底端将向左滑动多少米?
在杭州西湖风景游船处,如图,在离水面高度为5m的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为13m,此人以的速度收绳后船移动到点D的位置,问船向岸边移动了多少m?假设绳子是直的,结果保留根号
如图,把一块三角形土地挖去一个直角三角形后,测得米,米,米,米.求剩余土地图中阴影部分的面积.
扇形OAB是一个以O为圆心,半径为4千米且圆心角为的风景区,C是弧AB上的一个动点,CD、CE为风景区中的两条景观人行道,、,垂足分别为D,E,DE是风景区中的商业街,已知商业街每年能为风景区带来每千米200万元的经济效益,请问在C运动的过程中风景区商业街DE每年的经济效益是否为定值?如果是,求出该定值;如果不是,请说明理由.
答案
1.【答案】C
2.【答案】C
3.【答案】B
4.【答案】B
5.【答案】D
6.【答案】B
7.【答案】B
8.【答案】D
9.【答案】C
10.【答案】A
11.【答案】B
12.【答案】B
13.【答案】或
14.【答案】4
15.【答案】25
16.【答案】
17.【答案】8
18.【答案】16海里时
19.【答案】解:连接AC,
,,,
.
由,可得,
是直角三角形,
,,
故这块地的面积为.
20.【答案】解:连接AC,如图,
,
,
米,米,
米,
米,米,
,
为直角三角形,
这块草坪的面积米
21.【答案】解:村庄能否听到宣传,
理由:村庄A到公路MN的距离为600米米,
村庄能听到宣传;
如图:假设当宣讲车行驶到P点开始影响村庄,行驶QD点结束对村庄的影响,
则米,米,
米,
米,
影响村庄的时间为:分钟,
村庄总共能听到8分钟的宣传.
22.【答案】解:米,米,
梯子距离地面的高度米.
答:此时梯子顶端离地面24米;
梯子下滑了4米,即梯子距离地面的高度米,
,
米,即下端滑行了8米.
答:梯子底端将向左滑动了8米.
23.【答案】解:在中,,,,
,
此人以的速度收绳,10s后船移动到点D的位置,
,
,
.
答:船向岸边移动了.
24.【答案】解:在中,
米,米,米,米,
,
取正值.
在中,,.
,
为直角三角形,.
米
答:剩余土地图中阴影部分的面积为:96米.
25.【答案】解:结论:在C运动的过程中风景区商业街DE每年的经济效益是定值.
理由:如图,连接OC,交DE于J,取POC的中点K,连接DK,KE.
,,
,
,
,
,D,C,E四点共圆,
,
,
是定值,是定值,
弦DE的长是定值,
当点C是的中点时,千米,
此时,,
千米,
在C运动的过程中风景区商业街DE每年的经济效益是定值,
万元,
定值为万元.
第2页,共5页
第5页,共5页
