人教版九年级上册24.2.2(1)直线和圆的位置关系学案(表格式 无答案)
文档属性
| 名称 | 人教版九年级上册24.2.2(1)直线和圆的位置关系学案(表格式 无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 71.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-18 09:40:50 | ||
图片预览

文档简介
教师
科目
数学
学生
时间
教学内容
24.2直线和圆的位置关系
教学目标
1.能判定一条直线是否为圆的切线.2.会过圆上一点画圆的切线.
重点考点
1.通过判定一条直线是否为圆的切线,训练学生的推理判断能力.
教
学
实
施
过
程
教
学
实
施
过
程
一:作业检查
1、完成情况
:
优(
)
良(
)
差(
)
完成不好的原因:
考核复习(分数10分)
三、新课讲授
(一)知识点框架:
一、直线与圆的位置关系
直线与圆的位置关系由圆心到直线的距离d与圆的半径r的大小关系确定;
d>r直线与圆相离
d=r直线与圆相切
d二、切线的判定定理
1、切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线,用数学符号表示为:直线L⊥OA于点A,OA是○O的半径,则直线L是○O的切线。
2、切线的识别方法
(1)和圆只有一个公共点的直线是圆的切线
(2)到圆心的距离等于圆的半径的直线是圆的切线
(3)经过半径的外端且垂直于这条半径的直线是圆的切线
(二)例题
例1:已知Rt△ABC的斜边AB=8cm,AC=4cm.
(1)以点C为圆心作圆,当半径为多长时,AB与⊙C相切?
(2)以点C为圆心,分别以2cm和4cm的长为半径作两个圆,这两个圆与AB分别有怎样的位置关系?
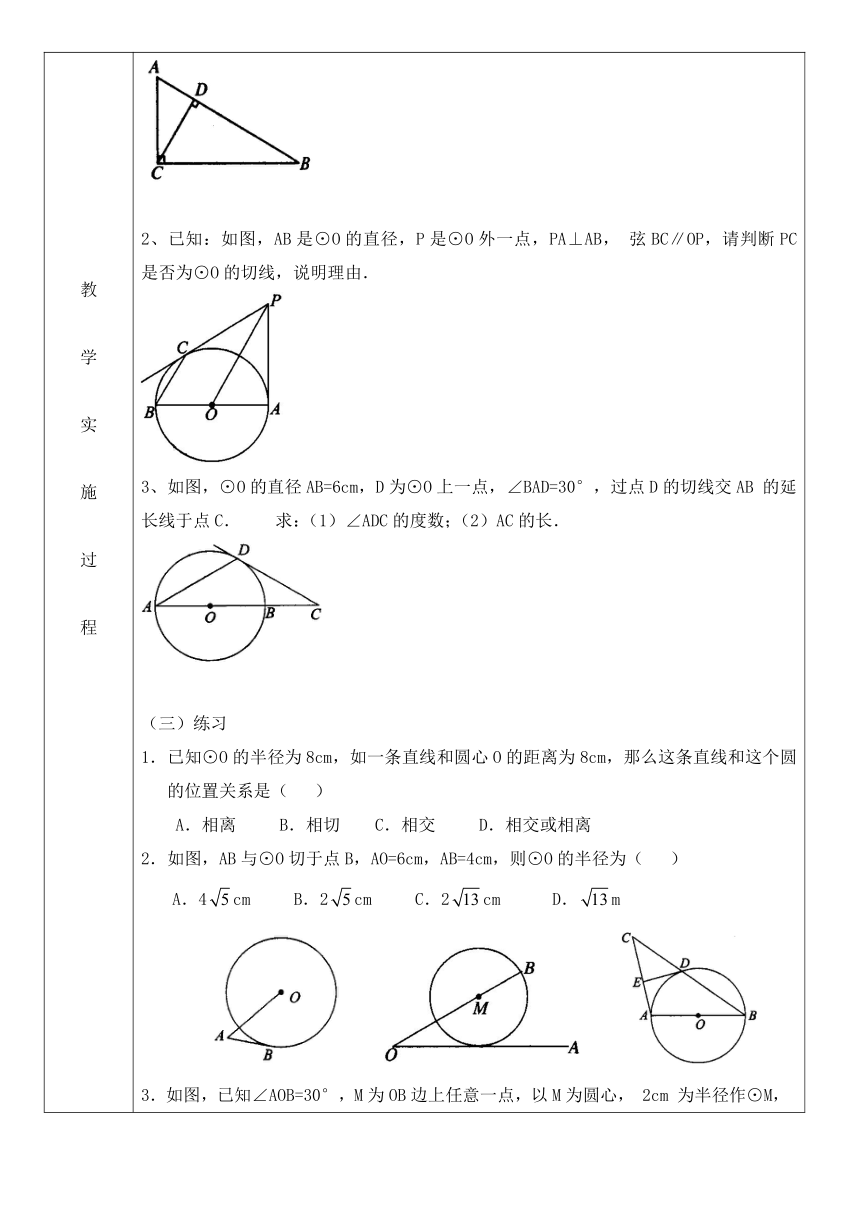
2、已知:如图,AB是⊙O的直径,P是⊙O外一点,PA⊥AB,弦BC∥OP,请判断PC是否为⊙O的切线,说明理由.
3、如图,⊙O的直径AB=6cm,D为⊙O上一点,∠BAD=30°,过点D的切线交AB的延长线于点C.
求:(1)∠ADC的度数;(2)AC的长.
(三)练习
1.已知⊙O的半径为8cm,如一条直线和圆心O的距离为8cm,那么这条直线和这个圆的位置关系是(
)
A.相离
B.相切
C.相交
D.相交或相离
2.如图,AB与⊙O切于点B,AO=6cm,AB=4cm,则⊙O的半径为(
)
A.4cm
B.2cm
C.2cm
D.m
3.如图,已知∠AOB=30°,M为OB边上任意一点,以M为圆心,2cm为半径作⊙M,当OM=______cm时,⊙M与OA相切.
4.已知:如图,AB为⊙O直径,BC交⊙O于点D,DE⊥AC于E,要使DE是⊙O的切线,那么图中的角应满足的条件为_______(只需填一个条件).
5.如图,直线AB切⊙O于点A,点C、D在⊙O上.
试探求:(1)当AD为⊙O的直径时,如图①,∠D与∠CAB的大小关系如何?并说明理由.
(2)当AD不为⊙O的直径时,如图②,∠D与∠CAB的大小关系同②一样吗?为什么?
(四)小结
证明一条直线是圆的切线的常见方法有两种:
当直线和圆只有一个公共点时,把圆心和这个公共点连接起来,然后证明直线垂直于这条半径,简称“作半径,证垂直”
当直线和圆的公共点没有明确时,可过圆心作直线的垂线,再证圆心到直线的距离等于半径,简称“作垂直,证半径”
四:学习检测(分数20分)
在Rt△ABC中,∠C=90°,∠A=60°,BC=4
cm,以点C为圆心,以3
cm长为半径作圆,则⊙C与AB的位置关系是____.
2、如图,△ABC的一边AB是○O的直径,请你添加一个条件,使BC是○O的切线,你所添加的条件为_____?。
3、如图,AB为○O的直径,EF切○O于点D,过点B作BH⊥EF于点H,交○O于点C,连接BD。
(1)求证:BD平分∠ABH。
(2)如果AB=12,BC=8,求圆心O到BC的距离。
4、如图,PA与○O相切,切点为A,PO交○O于点C,点B是优弧CBA上一点,若∠ABC=32°,则∠P的度数为_____?。
5、已知AB是○O的直径,直线BC与○O相切于点B,∠ABC的平分线BD交○O于点D,AD的延长线交BC于点C。
(1)求∠BAC的度数。
(2)求证:AD=CD。
科目
数学
学生
时间
教学内容
24.2直线和圆的位置关系
教学目标
1.能判定一条直线是否为圆的切线.2.会过圆上一点画圆的切线.
重点考点
1.通过判定一条直线是否为圆的切线,训练学生的推理判断能力.
教
学
实
施
过
程
教
学
实
施
过
程
一:作业检查
1、完成情况
:
优(
)
良(
)
差(
)
完成不好的原因:
考核复习(分数10分)
三、新课讲授
(一)知识点框架:
一、直线与圆的位置关系
直线与圆的位置关系由圆心到直线的距离d与圆的半径r的大小关系确定;
d>r直线与圆相离
d=r直线与圆相切
d
1、切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线,用数学符号表示为:直线L⊥OA于点A,OA是○O的半径,则直线L是○O的切线。
2、切线的识别方法
(1)和圆只有一个公共点的直线是圆的切线
(2)到圆心的距离等于圆的半径的直线是圆的切线
(3)经过半径的外端且垂直于这条半径的直线是圆的切线
(二)例题
例1:已知Rt△ABC的斜边AB=8cm,AC=4cm.
(1)以点C为圆心作圆,当半径为多长时,AB与⊙C相切?
(2)以点C为圆心,分别以2cm和4cm的长为半径作两个圆,这两个圆与AB分别有怎样的位置关系?
2、已知:如图,AB是⊙O的直径,P是⊙O外一点,PA⊥AB,弦BC∥OP,请判断PC是否为⊙O的切线,说明理由.
3、如图,⊙O的直径AB=6cm,D为⊙O上一点,∠BAD=30°,过点D的切线交AB的延长线于点C.
求:(1)∠ADC的度数;(2)AC的长.
(三)练习
1.已知⊙O的半径为8cm,如一条直线和圆心O的距离为8cm,那么这条直线和这个圆的位置关系是(
)
A.相离
B.相切
C.相交
D.相交或相离
2.如图,AB与⊙O切于点B,AO=6cm,AB=4cm,则⊙O的半径为(
)
A.4cm
B.2cm
C.2cm
D.m
3.如图,已知∠AOB=30°,M为OB边上任意一点,以M为圆心,2cm为半径作⊙M,当OM=______cm时,⊙M与OA相切.
4.已知:如图,AB为⊙O直径,BC交⊙O于点D,DE⊥AC于E,要使DE是⊙O的切线,那么图中的角应满足的条件为_______(只需填一个条件).
5.如图,直线AB切⊙O于点A,点C、D在⊙O上.
试探求:(1)当AD为⊙O的直径时,如图①,∠D与∠CAB的大小关系如何?并说明理由.
(2)当AD不为⊙O的直径时,如图②,∠D与∠CAB的大小关系同②一样吗?为什么?
(四)小结
证明一条直线是圆的切线的常见方法有两种:
当直线和圆只有一个公共点时,把圆心和这个公共点连接起来,然后证明直线垂直于这条半径,简称“作半径,证垂直”
当直线和圆的公共点没有明确时,可过圆心作直线的垂线,再证圆心到直线的距离等于半径,简称“作垂直,证半径”
四:学习检测(分数20分)
在Rt△ABC中,∠C=90°,∠A=60°,BC=4
cm,以点C为圆心,以3
cm长为半径作圆,则⊙C与AB的位置关系是____.
2、如图,△ABC的一边AB是○O的直径,请你添加一个条件,使BC是○O的切线,你所添加的条件为_____?。
3、如图,AB为○O的直径,EF切○O于点D,过点B作BH⊥EF于点H,交○O于点C,连接BD。
(1)求证:BD平分∠ABH。
(2)如果AB=12,BC=8,求圆心O到BC的距离。
4、如图,PA与○O相切,切点为A,PO交○O于点C,点B是优弧CBA上一点,若∠ABC=32°,则∠P的度数为_____?。
5、已知AB是○O的直径,直线BC与○O相切于点B,∠ABC的平分线BD交○O于点D,AD的延长线交BC于点C。
(1)求∠BAC的度数。
(2)求证:AD=CD。
同课章节目录
