湘教版九年级数学下册第2章:圆 单元基础拔高训练卷(word解析版)
文档属性
| 名称 | 湘教版九年级数学下册第2章:圆 单元基础拔高训练卷(word解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 906.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-18 06:41:28 | ||
图片预览



文档简介
九年级数学下册第2章圆单元基础拔高训练卷(湘教版)
一、单选题
1.以下命题:①经过三点一定可以作一个圆;
②优弧一定大于劣弧
③相等的弦所对的弧也相等;
④三角形的外心到三角形三个顶点的距离相等;其中正确的个数是(
)
A.4
B.3
C.2
D.1
2.如图,已知⊙O的两条弦AC,BD相交于点E,,,那么的度数为(
)
A.
B.
C.
D.
3.如图,是的内接三角形,是的直径,点在上.若,则的度数为(
)
A.
B.
C.
D.
4.如图,的半径为10,弦AB的长为16,M是弦AB上的动点,则线段OM长的最小值为(
)
A.4
B.6
C.8
D.10
5.下列命题中假命题的个数是(
)
①三点确定一个圆;②直径是圆中最长的弦;③相等的圆周角所对的弧相等;④平分弦的直径垂直于弦;⑤三角形的外心到三角形三个顶点的距离相等.
A.4
B.3
C.2
D.1
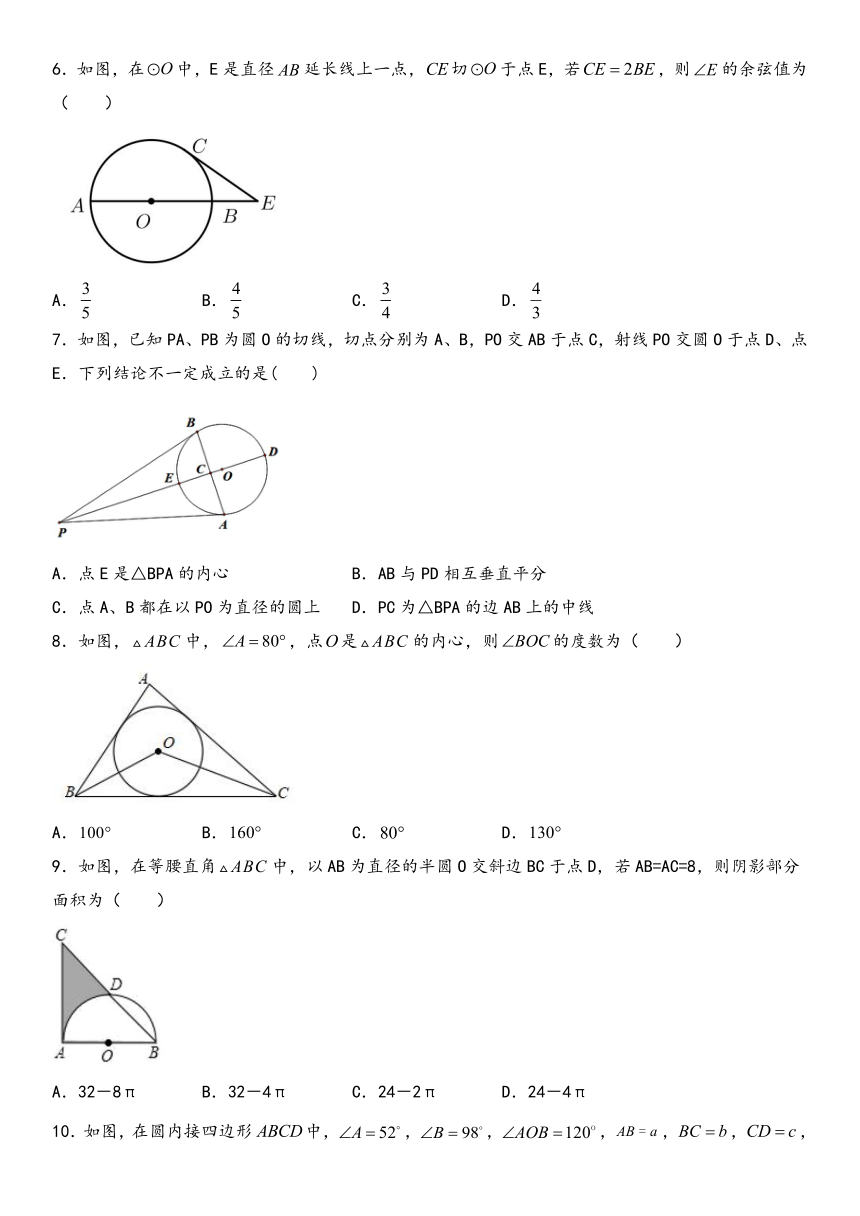
6.如图,在中,E是直径延长线上一点,切于点E,若,则的余弦值为(
)
A.
B.
C.
D.
7.如图,已知PA、PB为圆O的切线,切点分别为A、B,PO交AB于点C,射线PO交圆O于点D、点E.下列结论不一定成立的是( )
A.点E是△BPA的内心
B.AB与PD相互垂直平分
C.点A、B都在以PO为直径的圆上
D.PC为△BPA的边AB上的中线
8.如图,中,,点是的内心,则的度数为(
)
A.
B.
C.
D.
9.如图,在等腰直角中,以AB为直径的半圆O交斜边BC于点D,若AB=AC=8,则阴影部分面积为(
)
A.32-8π
B.32-4π
C.24-2π
D.24-4π
10.如图,在圆内接四边形中,,,,,,,,则此四边形的面积(用含a,b,c,d的代数式表示)为(
)
A.
B.
C.
D.
11.如图,在△ABC中,∠ACB=90°,过B,C两点的⊙O交AC于点D,交AB于点E,连接EO并延长交⊙O于点F.连接BF,CF.若∠EDC=135°,CF=,则AE2+BE2的值为
(
)
A.8
B.12
C.16
D.20
12.如图,点A,B分别在x轴、y轴上(OA>OB),以AB为直径的圆经过原点O,C是的中点,连结AC,BC.下列结论:①AC=BC;②若OA=4,OB=2,则△ABC的面积等于5;③若OA﹣OB=4,则点C的坐标是(2,﹣2).其中正确的结论有(
??)
A.3个
B.2个
C.1个
D.0个
二、填空题
13.如图,A、B、C为⊙O上三点,且∠ACB=35°,则∠OAB的度数是______度.
14.如图,在中,半径垂直于,则的半径是_____.
15.如图,直线AB与⊙O相切于点C,点D
是⊙O上的一点,且∠EDC=30°,则∠ECA的度数为_________.
16.如图,正五边形ABCDE内接于⊙O,若⊙O的半径为10,则的长为____.
17.如图,PA
、PB分别与⊙O相切于点A、B,⊙O的切线EF分别交PA、PB于点E、F,切点C在上,若PA长为2,则△PEF的周长是_____.
18.如图,四边形ABCD是⊙O的内接四边形,∠B=135°,则∠AOC的度数为_____.
19.如图,AB是⊙O的直径,且AB=4,点C是半圆AB上一动点(不与A,B重合),CD平分∠ACB交⊙O于点D,点
I是△ABC的内心,连接BD.下列结论:
①点D的位置随着动点C位置的变化而变化;
②ID=BD;
③OI的最小值为;
④ACBC=CD.
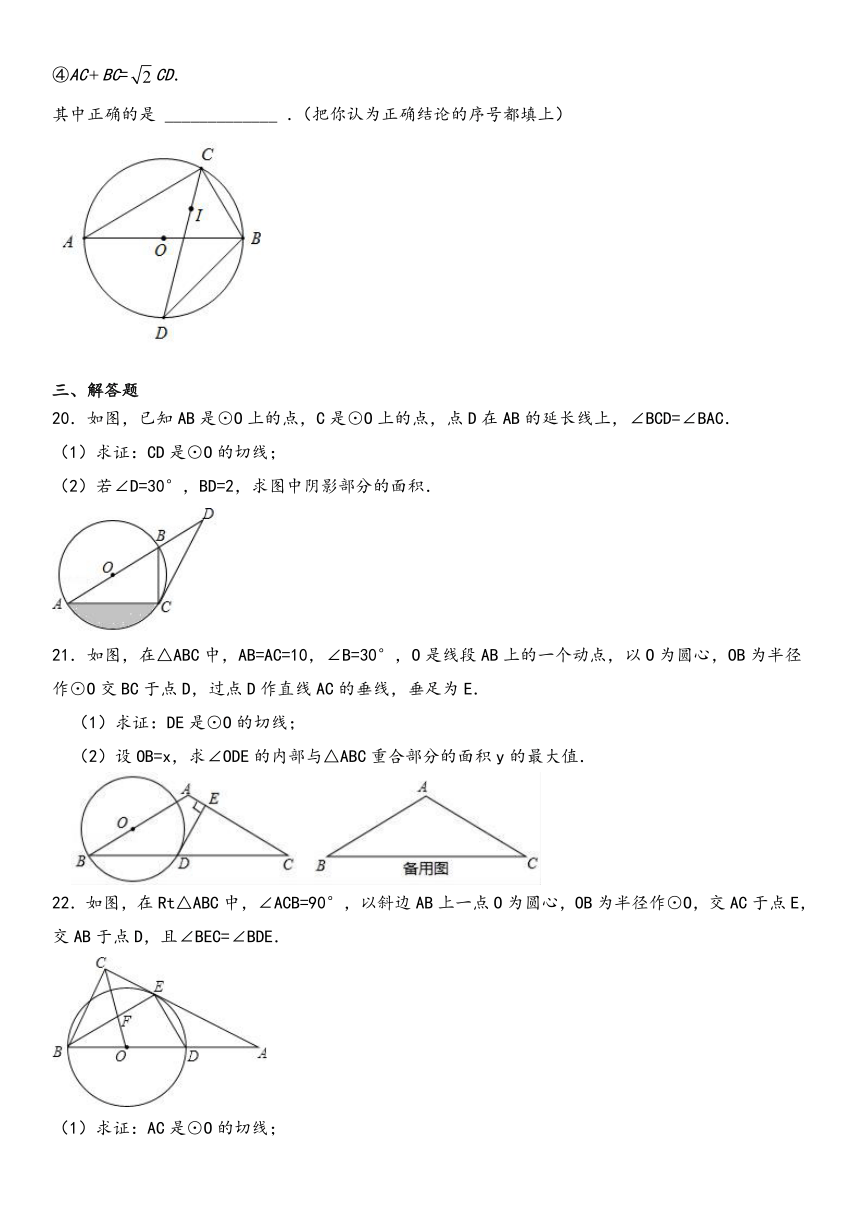
其中正确的是
_____________
.(把你认为正确结论的序号都填上)
三、解答题
20.如图,已知AB是⊙O上的点,C是⊙O上的点,点D在AB的延长线上,∠BCD=∠BAC.
(1)求证:CD是⊙O的切线;
(2)若∠D=30°,BD=2,求图中阴影部分的面积.
21.如图,在△ABC中,AB=AC=10,∠B=30°,O是线段AB上的一个动点,以O为圆心,OB为半径作⊙O交BC于点D,过点D作直线AC的垂线,垂足为E.
(1)求证:DE是⊙O的切线;
(2)设OB=x,求∠ODE的内部与△ABC重合部分的面积y的最大值.
22.如图,在Rt△ABC中,∠ACB=90°,以斜边AB上一点O为圆心,OB为半径作⊙O,交AC于点E,交AB于点D,且∠BEC=∠BDE.
(1)求证:AC是⊙O的切线;
(2)连接OC交BE于点F,若,求的值.
23.如图,AB是⊙O的直径,弦CD⊥AB于点E,点P⊙O上,∠1=∠C.
(1)求证:CB∥PD;
(2)若∠ABC=55°,求∠P的度数.
24.如图,在平面直角坐标系中,为原点,点坐标为,点坐标为,以为直径的圆与轴的负半轴交于点.
(1)求图象经过,,三点的抛物线的解析式;
(2)设点为所求抛物线的顶点,试判断直线与的关系,并说明理由.
25.如图,已知是的直径,点、在上,且,过点作,垂足为.
求的长;
若的延长线交于点,求弦、和弧围成的图形(阴影部分)的面积.
26.如图1,四边形ABCD内接于⊙O,AC为⊙O的直径,AC与BD交于点E,且AE=AB.
(1)DA=DB,求证:AB=CB;
(2)如图2,△ABC绕点C逆时针旋转30°得到△FGC,点A经过的路径为,若AC=4,求图中阴影部分面积S;
(3)在(2)的条件下,连接FB,求证:FB为⊙O的切线.
试卷第1页,总3页
参考答案
1.D
解:经过同一条直线的三个点,不可以作一个圆,故命题①错误;
不同圆的优弧就不一定大于劣弧,故命题②错误;
同圆或等圆中,相等的弦所对的弧也相等,但是如果不是同圆和等圆时,相等的弦所对的弧不一定相等,故命题③错误;
三角形的外心到三角形三个顶点的距离相等,故命题④正确;
2.C
由同弧所对的圆周角相等,得∠B=∠C=45°,
在中,∠A=75°,∠B=45°,
∴∠AEB=60°,
3.C
解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠BCD=36°,
∴∠ACD=90°-∠BCD=54°.
4.B
解:由题意得:根据点到直线垂线段最短,故线段OM长的最小值为当OM⊥AB时,连接OA,如图所示:
∵AB=16,
∴AM=MB=8,
∵OA=10,
∴在Rt△AOM中,,
∴OM的最小值为6;
5.B
解:①错误,三个不在同一直线上的点确定一个圆;
②正确;
③错误,同圆或等圆内,相等的圆周角所对的弧相等;
④错误;反例:两个直径互相平分但不一定垂直;
⑤正确;
∴假命题的个数是3.
6.B
解:如图,连接OC,
∵切于点E,
∴∠OCE=90°,
设OC=OB=x,,
∵在Rt中,,
∴,
解得,
∴,
∴,
故选:B.
7.B
解:如图,作EG⊥PA于G,EH⊥PB于H,作PO的中点F,并连结FB、FA、EB、EA、OB、OA,
由切线长定理可知PA=PB,∠BPO=∠APO,
∴△BPA为等腰三角形,且PC为△BPA的边AB上的中线,D不符合题意;
由切线的性质可知△OBP、△OAP为直角三角形,
∵F为PO的中点,∴FB=FA=,
∴点A、B都在以PO为直径的圆上,C不符合题意;
在△PBE和△PAE中,,
∴△PBE≌△PAE,∴EB=EA,∴∠EBA=∠EAB,
∵PA是⊙O的切线,∴∠PAE=∠EBA,∴∠PAE=∠EAB,∴EG=EC,
∵PO平分∠BPA,∴EH=EG,
∴EH=EG=EC,∴点E是△BPA的内心,A不符合题意;
∵PC=CD不一定成立,AB与PD不一定相互垂直平分,B符合题意;
8.D
解:∵,
∴,
∵点是的内心,
∴BO平分∠ABC,CO平分∠ACB,
∴,,
∴,
∴.
9.D
解:如图,连接AD、OD,
∵,
∴是等腰直角三角形,
∴,
∵AB是直径,
∴,
∴是等腰直角三角形,
∵,
∴,
∵,
∴,
∴
.
10.B
解:连接,交于,
,
,
,
,
,
,
,
,
在中,,,
,,
同理得:,,
,,
,
,
,
,
在中,由勾股定理得:,
,
,
,
,
,
,
,
,
故选B.
11.C
∵∠EDC=135°,
∴∠ADE=45°,∠ABC=180°-∠EDC
=180°-135°=45°;
∵∠ACB=90°,
∴∠A=45°,
∴∠ADE=∠A=45°,
∴AE=AD,∠AED=90°;
∵EF
为⊙O的直径,
∴∠FCE=90°,
∵∠ABC=∠EFC=45°,CF=,
∴EF=4;
连接BD,
∵∠AED=90°,
∴∠BED=90°,
∴BD
为⊙O的直径,
∴BD=4;
在Rt△BDE中,,
∴AE2+BE2=16.
故选C.
12.A
①∵AB为直径,
∴∠ACB=900,
∴①正确;
②∵C是的中点,
∴=,
∴AC=BC,
∴②正确;
③在Rt△AOB中,OA=4,OB=2,
∴AB==,
在Rt△ABC中,AC=BC=AB=,
∴△ABC的面积=×AC×BC=××=5,
∴③正确;
④如图,
过点C作CD⊥OA,DE⊥OB,
∴∠BEC=∠ADC=90°
在△BCE和△ACD中,,
∴△BCE≌△ACD,
∴AD=BE,CE=CD,
∵∠DOE=∠OEC=∠ODC=90°,
∴四边形ODCE是矩形,
∵CE=CD,
∴矩形ODCE是正方形,
∴OD=OD=CD=CE,
∵AD=OA?OD,BE=OB+BE=OB+OD,
∵AD=BE
∴OA?OD=OB+OD,
∵OA?OB=4,
∴OD=2,
∴CD=CE=2,
∴C(2,?2)
∴④正确,
13.55
解:∵OA=OB,
∴∠OAB=∠OBA,
∵∠ACB=35°,
∴∠AOB=2∠ACB=70°,
∴;
故答案为55.
14.5
设⊙O的半径为r,则OD=r-2,
∵OC⊥AB,
∴AD=BD=AB=4,
在Rt△AOD中,∵OD2+AD2=OA2,
∴(r-2)2+42=r2,解得r=5,
即⊙O的半径为5.
15.30°
解:如图所示,连接OE、OC,
∵∠EDC=30°,
∴∠EOC=2∠EDC=60°,
又∵OE=OC,
∴为等边三角形,
∴∠ECO=60°,
∵直线AB与圆O相切于点C,
∴∠ACO=90°,
∴∠ECA=∠ACO-∠ECO=90°-60°=30°.
16.2π
解:如图所示:连接OA、OB.
∵⊙O为正五边形ABCDE的外接圆,⊙O的半径为10,
∴∠AOB==72°,
∴的长为:.
故答案为:2π.
17.4.
解:∵PA、PB分别与⊙O相切于点A、B,
⊙O的切线EF分别交PA、PB于点E、F,切点C在上,
∴AE=CE,FB=CF,PA=PB=2,
∴△PEF的周长=PE+EF+PF=PA+PB=4.
18.
∵四边形ABCD是⊙O的内接四边形,∴∠B+∠D=180°,∴∠D=180°-135°=45°,∴∠AOC=90°,故答案为90°.
19.②④
解:
平分,AB是⊙O的直径,
,
,
是的直径,
是半圆的中点,即点是定点;
故①错误;
如图示,连接IB,
∵点I是△ABC的内心,
∴
又∵,
∴
即有
∴,
故②正确;
如图示,当OI最小时,经过圆心O,
过I点,作,交于点
∵点I是△ABC的内心,经过圆心O,
∴,
∵
∴是等腰直角三角形,
又∵,
∴,
设,则,,
∴,
解之得:,
即:,
故③错误;
假设,
∵点C是半圆AB上一动点,
则点C在半圆AB上对于任意位置上都满足,
如图示,
当经过圆心O时,,,
∴
与假设矛盾,故假设不成立,
∴
故④正确;
综上所述,正确的是②④,
故答案是:②④
20.
(1)如图,连接OC,∵OA=OC,∴∠BAC=∠OCA,∵∠BCD=∠BAC,∴∠BCD=∠OCA,∵AB是直径,∴∠ACB=90°,∴∠OCA+OCB=∠BCD+∠OCB=90°∴∠OCD=90°∵OC是半径,∴CD是⊙O的切线
(2)设⊙O的半径为r,∴AB=2r,∵∠D=30°,∠OCD=90°,∴OD=2r,∠COB=60°∴r+2=2r,∴r=2,∠AOC=120°∴BC=2,∴由勾股定理可知:AC=2,易求S△AOC=×2×1=S扇形OAC=,∴阴影部分面积为.
21.
证明:(1)连接OD,
∵AB=AC,
∴∠C=∠B.
∵OB=OD,
∴∠ODB=∠B
∴∠ODB=∠C
∴OD∥AC.
∵DE⊥AC,
∴OD⊥DE,
∴DE是⊙O的切线.
(2)①当点E在CA的延长线上时,设DE与AB交于点F,围成的图形为△ODF.
∵OD=
OB=
x,∠B=30°,
∴∠FOD=60°,
∵∠ODE=90°,
∴DF=
x,
∴S△ODF=
x·x=
,(0<x≤)
当x=时,S△ODF最大,最大值为;
②当点E在线段AC上时,围成的图形为梯形AODE.
∵AB=AC=10,∠B=30°,
∴BC=10,
作OH⊥BC,
∵OD=
OB=
x,∠B=30°,
∴BD=
2BH=
x,
∴CD=
10-x,
∵∠C=30°,∠DEC=90°,
∴DE=
(10-x),CE=
(10-x)=15-x,
∴AE=x-5,
∴S梯形AODE=
(x-5+
x)·
(10-x)=
(-+12
x-20)
(<x<10)
当x=6时,S梯形AODE最大,最大值为10;
综上所述,当x=6时,重合部分的面积最大,最大值为10.
22.
:解:(1)连接OE.
∵OB=OE,∴∠OBE=∠OEB.
∵∠ACB=90°,∴∠CBE+∠BEC=90°.
∵BD为⊙O的直径,∴∠BED=90°,∴∠DBE+∠BDE=90°,∴∠CBE=∠DBE,∴∠CBE=∠OEB,∴OE∥BC,∴∠OEA=∠ACB=90°,即OE⊥AC,∴AC为⊙O的切线.
(2)∵OE∥BC,∴△AOE∽△ABC,∴OE:BC=AE:AC.
∵CE:AE=2:3,∴AE:AC=3:5,∴OE:BC=3:5.
∵OE∥BC,∴△OEF∽△CBF,∴.
23
(1)要证明CB∥PD,只要证明∠1=∠P;由∠1=∠C,∠P=∠C,可得∠1=∠P,即可解决问题;
(2)在Rt△CEB中,求出∠C即可解决问题.
试题解析:(1)如图,∵∠1=∠C,∠P=∠C,
∴∠1=∠P,
∴CB∥PD;
(2)∵CD⊥AB,
∴∠CEB=90°,
∵∠CBE=55°,
∴∠C=90°﹣55°=35°,
∴∠P=∠C=35°.
24.
解:(1)连接AC、BC;
∵AB是⊙P的直径,
∴∠ACB=90°,即∠ACO+∠BCO=90°,
∵∠BCO+∠CBO=90°,
∴∠CBO=∠ACO,
∵∠AOC=∠BOC=90°,
∴△AOC∽△COB,
∴=,
∴OC2=OA·OB=16,
∴OC=4,
故C(0,﹣4),
设抛物线的解析式为:y=a(x+8)(x﹣2),
代入C点坐标得:a(0+8)(0﹣2)=﹣4,a=,
故抛物线的解析式为:y=(x+8)(x﹣2)=+x﹣4;
(2)由(1)知:y=+x﹣4=﹣;
则M(﹣3,﹣),
又∵C(0,?﹣4),P(﹣3,?0),
∴MP=,PC=5,MC=,
∴MP2=MC2+PC2,即△MPC是直角三角形,且∠PCM=90°,
故直线MC与⊙P相切.
25.
解:(1)
∵AB是⊙O的直径,
∴∠ACB=90°,
∵OE⊥AC,
∴OE?//?BC,
又∵点O是AB中点,
∴OE是△ABC的中位线,
∵∠D=60°,
∴∠B=60°,
又∵AB=6,
∴BC=AB·cos60°=3,
∴OE=
BC=;
(2)连接OC,
∵∠D=60°,
∴∠AOC=120°,
∵OF⊥AC,
∴AE=CE,=,
∴∠AOF=∠COF=60°,
∴△AOF为等边三角形,
∴AF=AO=CO,
∵在Rt△COE与Rt△AFE中,
,
∴△COE≌△AFE,
∴阴影部分的面积=扇形FOC的面积,
∵S扇形FOC==π.
∴阴影部分的面积为π.
26.
(1)证明:如图1中,
∵DA=DB,
∴∠DAB=∠DBA,
∵AE=AB,
∴∠AEB=∠ABE,
∴∠AEB=∠DAB,
∴∠EAD+∠ADE=∠EAD+∠EAB,
∴∠EAB=∠ADE,
∵∠ADE=∠ACB,
∴∠EAB=∠ACB,
∴AB=BC.
(2)如图2中,设AB的延长线交FG于M,连接CM,在BC上取一点N,使得CN=NM.
∵△ABC是等腰直角三角形,AC=4,
∴AB=BC=2,
∵BC=CG,CM=CM,
∴Rt△CBM≌Rt△CGM,
∴∠MCB=∠MCG=15°,
∵NC=NM,
∴∠NCM=∠NMC=15°,
∴∠MNB=30°,设BM=a,则MN=CN=2a,BN=a,
∴2a+a=2,
∴a=4﹣2,
∴S阴=2××BM×BC=(4﹣2)×=16﹣8.
(3)如图2﹣1中,连接OB、BF、作FH⊥AC于H.
∵∠ACF=30°,∠FHC=90°,
∴FH=CF=AC=OA=OB,
∵BA=BC,OA=OC,
∴BO⊥AC,
∴FH∥OB,
∴四边形OBFH是平行四边形,
∵∠BOH=90°,
∴四边形OBFH是矩形,
∴∠OBF=90°,即OB⊥BF;
∴BF是⊙O的切线.
一、单选题
1.以下命题:①经过三点一定可以作一个圆;
②优弧一定大于劣弧
③相等的弦所对的弧也相等;
④三角形的外心到三角形三个顶点的距离相等;其中正确的个数是(
)
A.4
B.3
C.2
D.1
2.如图,已知⊙O的两条弦AC,BD相交于点E,,,那么的度数为(
)
A.
B.
C.
D.
3.如图,是的内接三角形,是的直径,点在上.若,则的度数为(
)
A.
B.
C.
D.
4.如图,的半径为10,弦AB的长为16,M是弦AB上的动点,则线段OM长的最小值为(
)
A.4
B.6
C.8
D.10
5.下列命题中假命题的个数是(
)
①三点确定一个圆;②直径是圆中最长的弦;③相等的圆周角所对的弧相等;④平分弦的直径垂直于弦;⑤三角形的外心到三角形三个顶点的距离相等.
A.4
B.3
C.2
D.1
6.如图,在中,E是直径延长线上一点,切于点E,若,则的余弦值为(
)
A.
B.
C.
D.
7.如图,已知PA、PB为圆O的切线,切点分别为A、B,PO交AB于点C,射线PO交圆O于点D、点E.下列结论不一定成立的是( )
A.点E是△BPA的内心
B.AB与PD相互垂直平分
C.点A、B都在以PO为直径的圆上
D.PC为△BPA的边AB上的中线
8.如图,中,,点是的内心,则的度数为(
)
A.
B.
C.
D.
9.如图,在等腰直角中,以AB为直径的半圆O交斜边BC于点D,若AB=AC=8,则阴影部分面积为(
)
A.32-8π
B.32-4π
C.24-2π
D.24-4π
10.如图,在圆内接四边形中,,,,,,,,则此四边形的面积(用含a,b,c,d的代数式表示)为(
)
A.
B.
C.
D.
11.如图,在△ABC中,∠ACB=90°,过B,C两点的⊙O交AC于点D,交AB于点E,连接EO并延长交⊙O于点F.连接BF,CF.若∠EDC=135°,CF=,则AE2+BE2的值为
(
)
A.8
B.12
C.16
D.20
12.如图,点A,B分别在x轴、y轴上(OA>OB),以AB为直径的圆经过原点O,C是的中点,连结AC,BC.下列结论:①AC=BC;②若OA=4,OB=2,则△ABC的面积等于5;③若OA﹣OB=4,则点C的坐标是(2,﹣2).其中正确的结论有(
??)
A.3个
B.2个
C.1个
D.0个
二、填空题
13.如图,A、B、C为⊙O上三点,且∠ACB=35°,则∠OAB的度数是______度.
14.如图,在中,半径垂直于,则的半径是_____.
15.如图,直线AB与⊙O相切于点C,点D
是⊙O上的一点,且∠EDC=30°,则∠ECA的度数为_________.
16.如图,正五边形ABCDE内接于⊙O,若⊙O的半径为10,则的长为____.
17.如图,PA
、PB分别与⊙O相切于点A、B,⊙O的切线EF分别交PA、PB于点E、F,切点C在上,若PA长为2,则△PEF的周长是_____.
18.如图,四边形ABCD是⊙O的内接四边形,∠B=135°,则∠AOC的度数为_____.
19.如图,AB是⊙O的直径,且AB=4,点C是半圆AB上一动点(不与A,B重合),CD平分∠ACB交⊙O于点D,点
I是△ABC的内心,连接BD.下列结论:
①点D的位置随着动点C位置的变化而变化;
②ID=BD;
③OI的最小值为;
④ACBC=CD.
其中正确的是
_____________
.(把你认为正确结论的序号都填上)
三、解答题
20.如图,已知AB是⊙O上的点,C是⊙O上的点,点D在AB的延长线上,∠BCD=∠BAC.
(1)求证:CD是⊙O的切线;
(2)若∠D=30°,BD=2,求图中阴影部分的面积.
21.如图,在△ABC中,AB=AC=10,∠B=30°,O是线段AB上的一个动点,以O为圆心,OB为半径作⊙O交BC于点D,过点D作直线AC的垂线,垂足为E.
(1)求证:DE是⊙O的切线;
(2)设OB=x,求∠ODE的内部与△ABC重合部分的面积y的最大值.
22.如图,在Rt△ABC中,∠ACB=90°,以斜边AB上一点O为圆心,OB为半径作⊙O,交AC于点E,交AB于点D,且∠BEC=∠BDE.
(1)求证:AC是⊙O的切线;
(2)连接OC交BE于点F,若,求的值.
23.如图,AB是⊙O的直径,弦CD⊥AB于点E,点P⊙O上,∠1=∠C.
(1)求证:CB∥PD;
(2)若∠ABC=55°,求∠P的度数.
24.如图,在平面直角坐标系中,为原点,点坐标为,点坐标为,以为直径的圆与轴的负半轴交于点.
(1)求图象经过,,三点的抛物线的解析式;
(2)设点为所求抛物线的顶点,试判断直线与的关系,并说明理由.
25.如图,已知是的直径,点、在上,且,过点作,垂足为.
求的长;
若的延长线交于点,求弦、和弧围成的图形(阴影部分)的面积.
26.如图1,四边形ABCD内接于⊙O,AC为⊙O的直径,AC与BD交于点E,且AE=AB.
(1)DA=DB,求证:AB=CB;
(2)如图2,△ABC绕点C逆时针旋转30°得到△FGC,点A经过的路径为,若AC=4,求图中阴影部分面积S;
(3)在(2)的条件下,连接FB,求证:FB为⊙O的切线.
试卷第1页,总3页
参考答案
1.D
解:经过同一条直线的三个点,不可以作一个圆,故命题①错误;
不同圆的优弧就不一定大于劣弧,故命题②错误;
同圆或等圆中,相等的弦所对的弧也相等,但是如果不是同圆和等圆时,相等的弦所对的弧不一定相等,故命题③错误;
三角形的外心到三角形三个顶点的距离相等,故命题④正确;
2.C
由同弧所对的圆周角相等,得∠B=∠C=45°,
在中,∠A=75°,∠B=45°,
∴∠AEB=60°,
3.C
解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠BCD=36°,
∴∠ACD=90°-∠BCD=54°.
4.B
解:由题意得:根据点到直线垂线段最短,故线段OM长的最小值为当OM⊥AB时,连接OA,如图所示:
∵AB=16,
∴AM=MB=8,
∵OA=10,
∴在Rt△AOM中,,
∴OM的最小值为6;
5.B
解:①错误,三个不在同一直线上的点确定一个圆;
②正确;
③错误,同圆或等圆内,相等的圆周角所对的弧相等;
④错误;反例:两个直径互相平分但不一定垂直;
⑤正确;
∴假命题的个数是3.
6.B
解:如图,连接OC,
∵切于点E,
∴∠OCE=90°,
设OC=OB=x,,
∵在Rt中,,
∴,
解得,
∴,
∴,
故选:B.
7.B
解:如图,作EG⊥PA于G,EH⊥PB于H,作PO的中点F,并连结FB、FA、EB、EA、OB、OA,
由切线长定理可知PA=PB,∠BPO=∠APO,
∴△BPA为等腰三角形,且PC为△BPA的边AB上的中线,D不符合题意;
由切线的性质可知△OBP、△OAP为直角三角形,
∵F为PO的中点,∴FB=FA=,
∴点A、B都在以PO为直径的圆上,C不符合题意;
在△PBE和△PAE中,,
∴△PBE≌△PAE,∴EB=EA,∴∠EBA=∠EAB,
∵PA是⊙O的切线,∴∠PAE=∠EBA,∴∠PAE=∠EAB,∴EG=EC,
∵PO平分∠BPA,∴EH=EG,
∴EH=EG=EC,∴点E是△BPA的内心,A不符合题意;
∵PC=CD不一定成立,AB与PD不一定相互垂直平分,B符合题意;
8.D
解:∵,
∴,
∵点是的内心,
∴BO平分∠ABC,CO平分∠ACB,
∴,,
∴,
∴.
9.D
解:如图,连接AD、OD,
∵,
∴是等腰直角三角形,
∴,
∵AB是直径,
∴,
∴是等腰直角三角形,
∵,
∴,
∵,
∴,
∴
.
10.B
解:连接,交于,
,
,
,
,
,
,
,
,
在中,,,
,,
同理得:,,
,,
,
,
,
,
在中,由勾股定理得:,
,
,
,
,
,
,
,
,
故选B.
11.C
∵∠EDC=135°,
∴∠ADE=45°,∠ABC=180°-∠EDC
=180°-135°=45°;
∵∠ACB=90°,
∴∠A=45°,
∴∠ADE=∠A=45°,
∴AE=AD,∠AED=90°;
∵EF
为⊙O的直径,
∴∠FCE=90°,
∵∠ABC=∠EFC=45°,CF=,
∴EF=4;
连接BD,
∵∠AED=90°,
∴∠BED=90°,
∴BD
为⊙O的直径,
∴BD=4;
在Rt△BDE中,,
∴AE2+BE2=16.
故选C.
12.A
①∵AB为直径,
∴∠ACB=900,
∴①正确;
②∵C是的中点,
∴=,
∴AC=BC,
∴②正确;
③在Rt△AOB中,OA=4,OB=2,
∴AB==,
在Rt△ABC中,AC=BC=AB=,
∴△ABC的面积=×AC×BC=××=5,
∴③正确;
④如图,
过点C作CD⊥OA,DE⊥OB,
∴∠BEC=∠ADC=90°
在△BCE和△ACD中,,
∴△BCE≌△ACD,
∴AD=BE,CE=CD,
∵∠DOE=∠OEC=∠ODC=90°,
∴四边形ODCE是矩形,
∵CE=CD,
∴矩形ODCE是正方形,
∴OD=OD=CD=CE,
∵AD=OA?OD,BE=OB+BE=OB+OD,
∵AD=BE
∴OA?OD=OB+OD,
∵OA?OB=4,
∴OD=2,
∴CD=CE=2,
∴C(2,?2)
∴④正确,
13.55
解:∵OA=OB,
∴∠OAB=∠OBA,
∵∠ACB=35°,
∴∠AOB=2∠ACB=70°,
∴;
故答案为55.
14.5
设⊙O的半径为r,则OD=r-2,
∵OC⊥AB,
∴AD=BD=AB=4,
在Rt△AOD中,∵OD2+AD2=OA2,
∴(r-2)2+42=r2,解得r=5,
即⊙O的半径为5.
15.30°
解:如图所示,连接OE、OC,
∵∠EDC=30°,
∴∠EOC=2∠EDC=60°,
又∵OE=OC,
∴为等边三角形,
∴∠ECO=60°,
∵直线AB与圆O相切于点C,
∴∠ACO=90°,
∴∠ECA=∠ACO-∠ECO=90°-60°=30°.
16.2π
解:如图所示:连接OA、OB.
∵⊙O为正五边形ABCDE的外接圆,⊙O的半径为10,
∴∠AOB==72°,
∴的长为:.
故答案为:2π.
17.4.
解:∵PA、PB分别与⊙O相切于点A、B,
⊙O的切线EF分别交PA、PB于点E、F,切点C在上,
∴AE=CE,FB=CF,PA=PB=2,
∴△PEF的周长=PE+EF+PF=PA+PB=4.
18.
∵四边形ABCD是⊙O的内接四边形,∴∠B+∠D=180°,∴∠D=180°-135°=45°,∴∠AOC=90°,故答案为90°.
19.②④
解:
平分,AB是⊙O的直径,
,
,
是的直径,
是半圆的中点,即点是定点;
故①错误;
如图示,连接IB,
∵点I是△ABC的内心,
∴
又∵,
∴
即有
∴,
故②正确;
如图示,当OI最小时,经过圆心O,
过I点,作,交于点
∵点I是△ABC的内心,经过圆心O,
∴,
∵
∴是等腰直角三角形,
又∵,
∴,
设,则,,
∴,
解之得:,
即:,
故③错误;
假设,
∵点C是半圆AB上一动点,
则点C在半圆AB上对于任意位置上都满足,
如图示,
当经过圆心O时,,,
∴
与假设矛盾,故假设不成立,
∴
故④正确;
综上所述,正确的是②④,
故答案是:②④
20.
(1)如图,连接OC,∵OA=OC,∴∠BAC=∠OCA,∵∠BCD=∠BAC,∴∠BCD=∠OCA,∵AB是直径,∴∠ACB=90°,∴∠OCA+OCB=∠BCD+∠OCB=90°∴∠OCD=90°∵OC是半径,∴CD是⊙O的切线
(2)设⊙O的半径为r,∴AB=2r,∵∠D=30°,∠OCD=90°,∴OD=2r,∠COB=60°∴r+2=2r,∴r=2,∠AOC=120°∴BC=2,∴由勾股定理可知:AC=2,易求S△AOC=×2×1=S扇形OAC=,∴阴影部分面积为.
21.
证明:(1)连接OD,
∵AB=AC,
∴∠C=∠B.
∵OB=OD,
∴∠ODB=∠B
∴∠ODB=∠C
∴OD∥AC.
∵DE⊥AC,
∴OD⊥DE,
∴DE是⊙O的切线.
(2)①当点E在CA的延长线上时,设DE与AB交于点F,围成的图形为△ODF.
∵OD=
OB=
x,∠B=30°,
∴∠FOD=60°,
∵∠ODE=90°,
∴DF=
x,
∴S△ODF=
x·x=
,(0<x≤)
当x=时,S△ODF最大,最大值为;
②当点E在线段AC上时,围成的图形为梯形AODE.
∵AB=AC=10,∠B=30°,
∴BC=10,
作OH⊥BC,
∵OD=
OB=
x,∠B=30°,
∴BD=
2BH=
x,
∴CD=
10-x,
∵∠C=30°,∠DEC=90°,
∴DE=
(10-x),CE=
(10-x)=15-x,
∴AE=x-5,
∴S梯形AODE=
(x-5+
x)·
(10-x)=
(-+12
x-20)
(<x<10)
当x=6时,S梯形AODE最大,最大值为10;
综上所述,当x=6时,重合部分的面积最大,最大值为10.
22.
:解:(1)连接OE.
∵OB=OE,∴∠OBE=∠OEB.
∵∠ACB=90°,∴∠CBE+∠BEC=90°.
∵BD为⊙O的直径,∴∠BED=90°,∴∠DBE+∠BDE=90°,∴∠CBE=∠DBE,∴∠CBE=∠OEB,∴OE∥BC,∴∠OEA=∠ACB=90°,即OE⊥AC,∴AC为⊙O的切线.
(2)∵OE∥BC,∴△AOE∽△ABC,∴OE:BC=AE:AC.
∵CE:AE=2:3,∴AE:AC=3:5,∴OE:BC=3:5.
∵OE∥BC,∴△OEF∽△CBF,∴.
23
(1)要证明CB∥PD,只要证明∠1=∠P;由∠1=∠C,∠P=∠C,可得∠1=∠P,即可解决问题;
(2)在Rt△CEB中,求出∠C即可解决问题.
试题解析:(1)如图,∵∠1=∠C,∠P=∠C,
∴∠1=∠P,
∴CB∥PD;
(2)∵CD⊥AB,
∴∠CEB=90°,
∵∠CBE=55°,
∴∠C=90°﹣55°=35°,
∴∠P=∠C=35°.
24.
解:(1)连接AC、BC;
∵AB是⊙P的直径,
∴∠ACB=90°,即∠ACO+∠BCO=90°,
∵∠BCO+∠CBO=90°,
∴∠CBO=∠ACO,
∵∠AOC=∠BOC=90°,
∴△AOC∽△COB,
∴=,
∴OC2=OA·OB=16,
∴OC=4,
故C(0,﹣4),
设抛物线的解析式为:y=a(x+8)(x﹣2),
代入C点坐标得:a(0+8)(0﹣2)=﹣4,a=,
故抛物线的解析式为:y=(x+8)(x﹣2)=+x﹣4;
(2)由(1)知:y=+x﹣4=﹣;
则M(﹣3,﹣),
又∵C(0,?﹣4),P(﹣3,?0),
∴MP=,PC=5,MC=,
∴MP2=MC2+PC2,即△MPC是直角三角形,且∠PCM=90°,
故直线MC与⊙P相切.
25.
解:(1)
∵AB是⊙O的直径,
∴∠ACB=90°,
∵OE⊥AC,
∴OE?//?BC,
又∵点O是AB中点,
∴OE是△ABC的中位线,
∵∠D=60°,
∴∠B=60°,
又∵AB=6,
∴BC=AB·cos60°=3,
∴OE=
BC=;
(2)连接OC,
∵∠D=60°,
∴∠AOC=120°,
∵OF⊥AC,
∴AE=CE,=,
∴∠AOF=∠COF=60°,
∴△AOF为等边三角形,
∴AF=AO=CO,
∵在Rt△COE与Rt△AFE中,
,
∴△COE≌△AFE,
∴阴影部分的面积=扇形FOC的面积,
∵S扇形FOC==π.
∴阴影部分的面积为π.
26.
(1)证明:如图1中,
∵DA=DB,
∴∠DAB=∠DBA,
∵AE=AB,
∴∠AEB=∠ABE,
∴∠AEB=∠DAB,
∴∠EAD+∠ADE=∠EAD+∠EAB,
∴∠EAB=∠ADE,
∵∠ADE=∠ACB,
∴∠EAB=∠ACB,
∴AB=BC.
(2)如图2中,设AB的延长线交FG于M,连接CM,在BC上取一点N,使得CN=NM.
∵△ABC是等腰直角三角形,AC=4,
∴AB=BC=2,
∵BC=CG,CM=CM,
∴Rt△CBM≌Rt△CGM,
∴∠MCB=∠MCG=15°,
∵NC=NM,
∴∠NCM=∠NMC=15°,
∴∠MNB=30°,设BM=a,则MN=CN=2a,BN=a,
∴2a+a=2,
∴a=4﹣2,
∴S阴=2××BM×BC=(4﹣2)×=16﹣8.
(3)如图2﹣1中,连接OB、BF、作FH⊥AC于H.
∵∠ACF=30°,∠FHC=90°,
∴FH=CF=AC=OA=OB,
∵BA=BC,OA=OC,
∴BO⊥AC,
∴FH∥OB,
∴四边形OBFH是平行四边形,
∵∠BOH=90°,
∴四边形OBFH是矩形,
∴∠OBF=90°,即OB⊥BF;
∴BF是⊙O的切线.
