人教版七年级数学下册知识双清练:5.2.2 平行线的判定(Word版 含答案)
文档属性
| 名称 | 人教版七年级数学下册知识双清练:5.2.2 平行线的判定(Word版 含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 180.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-18 10:18:58 | ||
图片预览


文档简介
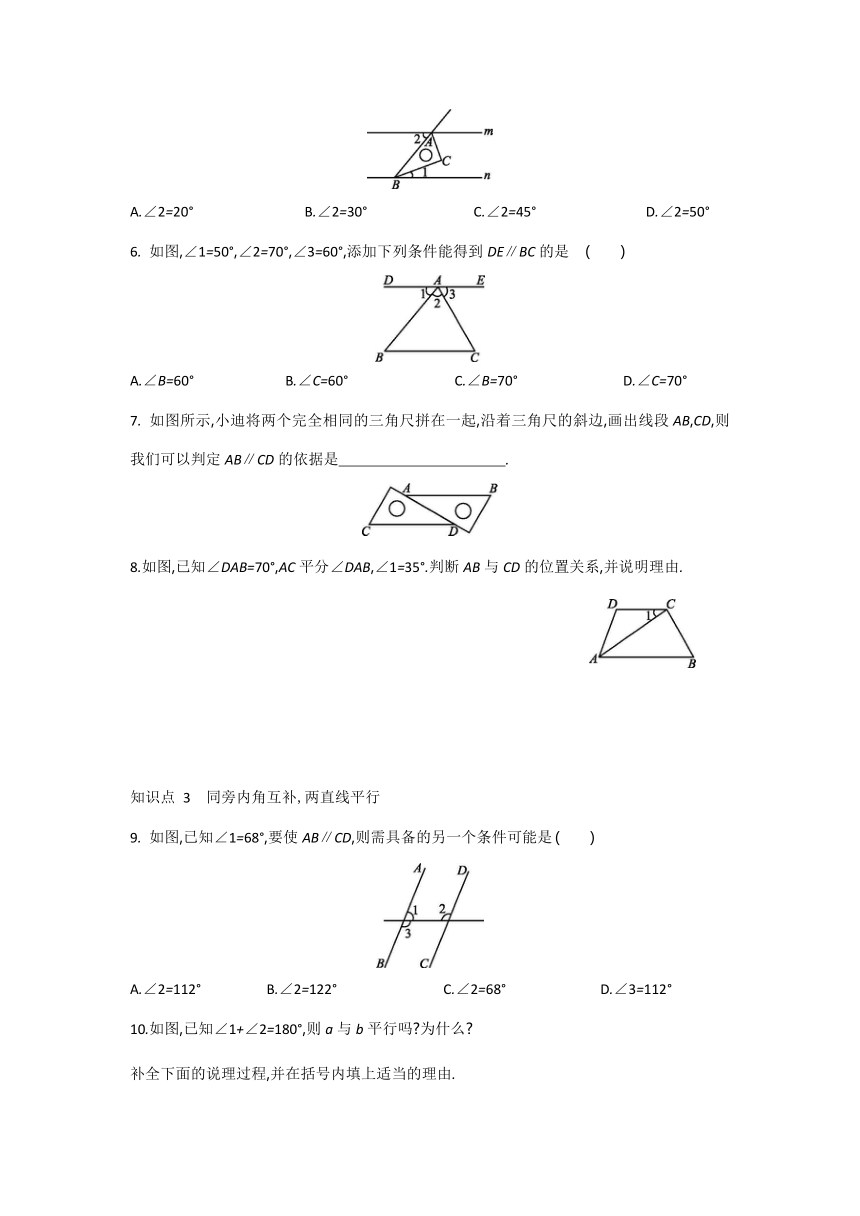
5.2.2 平行线的判定
练知识点
知识点
1 同位角相等,两直线平行
1.
如图,∠1=120°,要使a∥b,则∠2的大小是
( )
A.60°
B.80°
C.100°
D.120°
2.如图是利用直尺和三角尺过已知直线l外一点P作直线l的平行线的方法,其理由是 .?
3.
如图,将木条a,b与c钉在一起,∠1=70°,∠2=50°,要使木条a与b平行,则木条a顺时针旋转的度数至少是 .?
4.如图,∠3与∠1互余,∠3与∠2互余.试说明:AB∥CD.
知识点
2 内错角相等,两直线平行
5.将一块三角尺按图所示方式放置,其中∠ABC=30°,A,B两点分别落在直线m,n上,∠1=20°,添加下列哪一个条件可使直线m∥n
( )
A.∠2=20°
B.∠2=30°
C.∠2=45°
D.∠2=50°
6.
如图,∠1=50°,∠2=70°,∠3=60°,添加下列条件能得到DE∥BC的是
( )
A.∠B=60°
B.∠C=60°
C.∠B=70°
D.∠C=70°
7.
如图所示,小迪将两个完全相同的三角尺拼在一起,沿着三角尺的斜边,画出线段AB,CD,则我们可以判定AB∥CD的依据是 .?
8.如图,已知∠DAB=70°,AC平分∠DAB,∠1=35°.判断AB与CD的位置关系,并说明理由.
知识点
3 同旁内角互补,两直线平行
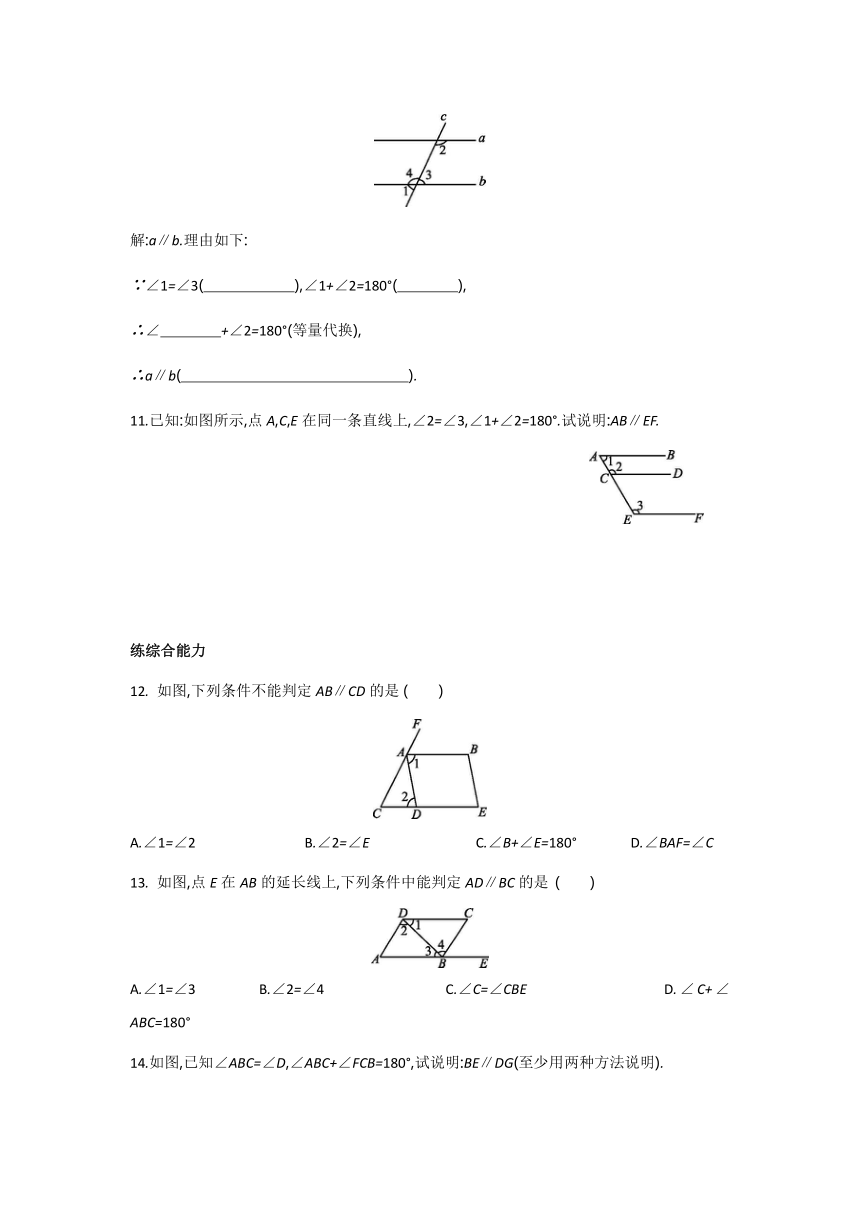
9.
如图,已知∠1=68°,要使AB∥CD,则需具备的另一个条件可能是
( )
A.∠2=112°
B.∠2=122°
C.∠2=68°
D.∠3=112°
10.如图,已知∠1+∠2=180°,则a与b平行吗?为什么?
补全下面的说理过程,并在括号内填上适当的理由.
解:a∥b.理由如下:
∵∠1=∠3( ),∠1+∠2=180°( ),?
∴∠ +∠2=180°(等量代换),?
∴a∥b( ).?
11.已知:如图所示,点A,C,E在同一条直线上,∠2=∠3,∠1+∠2=180°.试说明:AB∥EF.
练综合能力
12.
如图,下列条件不能判定AB∥CD的是
( )
A.∠1=∠2
B.∠2=∠E
C.∠B+∠E=180°
D.∠BAF=∠C
13.
如图,点E在AB的延长线上,下列条件中能判定AD∥BC的是
( )
A.∠1=∠3
B.∠2=∠4
C.∠C=∠CBE
D.∠C+∠ABC=180°
14.如图,已知∠ABC=∠D,∠ABC+∠FCB=180°,试说明:BE∥DG(至少用两种方法说明).
15.
已知:如图,直线AB,CD与直线EF分别相交于点M,N,MP平分∠AMF,NQ平分∠END,若∠AME=∠DNF,试说明:MP∥NQ.
16.阅读材料:光线反射时,反射光线、入射光线和法线在同一平面内,反射光线、入射光线分别在法线两侧,反射角等于入射角.如图①,EF为一镜面,AO为入射光线,入射点为点O,ON为法线(过入射点O且垂直于镜面EF的直线),OB为反射光线,此时反射角∠BON(反射光线与法线的夹角)等于入射角∠AON(入射光线与法线的夹角).
解决问题:如图②,两平面镜OP,OQ相交于点O,一束光线从点A出发,经过平面镜两次反射后,恰好经过点D.当∠POQ为多少度时,光线AB∥CD?请说明理由.
参考答案
1.D
2.同位角相等,两直线平行 解析:
由作平行线的过程可知,三角尺移动前后的60°角为同位角,根据“同位角相等,两直线平行”的判定条件,可得过点P的直线与直线l平行.
3.20° 解析:
当∠AOB=∠2=50°时,木条a与b平行,此时木条a旋转的度数是∠AOC=∠1-
∠AOB=20°.
4.解:∵∠3与∠1互余,∠3与∠2互余,
∴∠1=∠2,∴AB∥CD.
5.D
6.B 解析:
∵∠1=50°,∠2=70°,∠3=60°,∴欲使DE∥BC,则需∠B=∠1=50°或∠C=∠3=60°.
7.内错角相等,两直线平行
8.解:AB∥CD.
理由:∵∠DAB=70°,AC平分∠DAB,
∴∠CAB=∠DAB=35°.
又∵∠1=35°,∴∠1=∠CAB,
∴AB∥CD.
9.A
10.对顶角相等 已知 3 同旁内角互补,两直线平行
11.解:∵∠2=∠3,∠1+∠2=180°(已知),
∴∠1+∠3=180°(等量代换),
∴AB∥EF(同旁内角互补,两直线平行).
12.B 13.B
14.解:方法一:∵∠ABC=∠D,∠ABC+∠FCB=180°(已知),
∴∠D+∠FCB=180°(等量代换).
∵∠ECD=∠FCB(对顶角相等),
∴∠D+∠ECD=180°(等量代换),
∴BE∥DG(同旁内角互补,两直线平行).
方法二:∵∠ABC+∠FCB=180°,∠BCD+∠FCB=180°(已知),
∴∠ABC=∠BCD(同角的补角相等).
∵∠ABC=∠D(已知),
∴∠BCD=∠D(等量代换),
∴BE∥DG(内错角相等,两直线平行).
15.解:∵∠AME=∠DNF,∠AME+∠AMF=∠DNF+∠END=180°,
∴∠AMF=∠END.
∵MP平分∠AMF,NQ平分∠END,
∴∠PMN=∠AMF,∠QNM=∠END,
∴∠PMN=∠QNM,
∴MP∥NQ.
16.解:设∠ABP=∠OBC=α,∠BCO=∠DCQ=β,则∠ABC=180°-2α,∠BCD=180°-2β.
当AB∥CD时,∠ABC+∠BCD=180°,
即180°-2α+180°-2β=180°,
∴180°=2(α+β),
∴α+β=90°,
∴∠POQ=180°-∠OBC-∠BCO=180°-(α+β)=90°,
∴当∠POQ为90°时,光线AB∥CD.
练知识点
知识点
1 同位角相等,两直线平行
1.
如图,∠1=120°,要使a∥b,则∠2的大小是
( )
A.60°
B.80°
C.100°
D.120°
2.如图是利用直尺和三角尺过已知直线l外一点P作直线l的平行线的方法,其理由是 .?
3.
如图,将木条a,b与c钉在一起,∠1=70°,∠2=50°,要使木条a与b平行,则木条a顺时针旋转的度数至少是 .?
4.如图,∠3与∠1互余,∠3与∠2互余.试说明:AB∥CD.
知识点
2 内错角相等,两直线平行
5.将一块三角尺按图所示方式放置,其中∠ABC=30°,A,B两点分别落在直线m,n上,∠1=20°,添加下列哪一个条件可使直线m∥n
( )
A.∠2=20°
B.∠2=30°
C.∠2=45°
D.∠2=50°
6.
如图,∠1=50°,∠2=70°,∠3=60°,添加下列条件能得到DE∥BC的是
( )
A.∠B=60°
B.∠C=60°
C.∠B=70°
D.∠C=70°
7.
如图所示,小迪将两个完全相同的三角尺拼在一起,沿着三角尺的斜边,画出线段AB,CD,则我们可以判定AB∥CD的依据是 .?
8.如图,已知∠DAB=70°,AC平分∠DAB,∠1=35°.判断AB与CD的位置关系,并说明理由.
知识点
3 同旁内角互补,两直线平行
9.
如图,已知∠1=68°,要使AB∥CD,则需具备的另一个条件可能是
( )
A.∠2=112°
B.∠2=122°
C.∠2=68°
D.∠3=112°
10.如图,已知∠1+∠2=180°,则a与b平行吗?为什么?
补全下面的说理过程,并在括号内填上适当的理由.
解:a∥b.理由如下:
∵∠1=∠3( ),∠1+∠2=180°( ),?
∴∠ +∠2=180°(等量代换),?
∴a∥b( ).?
11.已知:如图所示,点A,C,E在同一条直线上,∠2=∠3,∠1+∠2=180°.试说明:AB∥EF.
练综合能力
12.
如图,下列条件不能判定AB∥CD的是
( )
A.∠1=∠2
B.∠2=∠E
C.∠B+∠E=180°
D.∠BAF=∠C
13.
如图,点E在AB的延长线上,下列条件中能判定AD∥BC的是
( )
A.∠1=∠3
B.∠2=∠4
C.∠C=∠CBE
D.∠C+∠ABC=180°
14.如图,已知∠ABC=∠D,∠ABC+∠FCB=180°,试说明:BE∥DG(至少用两种方法说明).
15.
已知:如图,直线AB,CD与直线EF分别相交于点M,N,MP平分∠AMF,NQ平分∠END,若∠AME=∠DNF,试说明:MP∥NQ.
16.阅读材料:光线反射时,反射光线、入射光线和法线在同一平面内,反射光线、入射光线分别在法线两侧,反射角等于入射角.如图①,EF为一镜面,AO为入射光线,入射点为点O,ON为法线(过入射点O且垂直于镜面EF的直线),OB为反射光线,此时反射角∠BON(反射光线与法线的夹角)等于入射角∠AON(入射光线与法线的夹角).
解决问题:如图②,两平面镜OP,OQ相交于点O,一束光线从点A出发,经过平面镜两次反射后,恰好经过点D.当∠POQ为多少度时,光线AB∥CD?请说明理由.
参考答案
1.D
2.同位角相等,两直线平行 解析:
由作平行线的过程可知,三角尺移动前后的60°角为同位角,根据“同位角相等,两直线平行”的判定条件,可得过点P的直线与直线l平行.
3.20° 解析:
当∠AOB=∠2=50°时,木条a与b平行,此时木条a旋转的度数是∠AOC=∠1-
∠AOB=20°.
4.解:∵∠3与∠1互余,∠3与∠2互余,
∴∠1=∠2,∴AB∥CD.
5.D
6.B 解析:
∵∠1=50°,∠2=70°,∠3=60°,∴欲使DE∥BC,则需∠B=∠1=50°或∠C=∠3=60°.
7.内错角相等,两直线平行
8.解:AB∥CD.
理由:∵∠DAB=70°,AC平分∠DAB,
∴∠CAB=∠DAB=35°.
又∵∠1=35°,∴∠1=∠CAB,
∴AB∥CD.
9.A
10.对顶角相等 已知 3 同旁内角互补,两直线平行
11.解:∵∠2=∠3,∠1+∠2=180°(已知),
∴∠1+∠3=180°(等量代换),
∴AB∥EF(同旁内角互补,两直线平行).
12.B 13.B
14.解:方法一:∵∠ABC=∠D,∠ABC+∠FCB=180°(已知),
∴∠D+∠FCB=180°(等量代换).
∵∠ECD=∠FCB(对顶角相等),
∴∠D+∠ECD=180°(等量代换),
∴BE∥DG(同旁内角互补,两直线平行).
方法二:∵∠ABC+∠FCB=180°,∠BCD+∠FCB=180°(已知),
∴∠ABC=∠BCD(同角的补角相等).
∵∠ABC=∠D(已知),
∴∠BCD=∠D(等量代换),
∴BE∥DG(内错角相等,两直线平行).
15.解:∵∠AME=∠DNF,∠AME+∠AMF=∠DNF+∠END=180°,
∴∠AMF=∠END.
∵MP平分∠AMF,NQ平分∠END,
∴∠PMN=∠AMF,∠QNM=∠END,
∴∠PMN=∠QNM,
∴MP∥NQ.
16.解:设∠ABP=∠OBC=α,∠BCO=∠DCQ=β,则∠ABC=180°-2α,∠BCD=180°-2β.
当AB∥CD时,∠ABC+∠BCD=180°,
即180°-2α+180°-2β=180°,
∴180°=2(α+β),
∴α+β=90°,
∴∠POQ=180°-∠OBC-∠BCO=180°-(α+β)=90°,
∴当∠POQ为90°时,光线AB∥CD.
