人教版数学七年级下册 9.1.2 不等式的性质 课件(28张)
文档属性
| 名称 | 人教版数学七年级下册 9.1.2 不等式的性质 课件(28张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-17 00:00:00 | ||
图片预览







文档简介
第九章 不等式与不等式组
9.1 不等式
9.1.2 不等式的性质
1.理解并掌握不等式的基本性质;
2.通过实例操作,培养学生观察、分析、比较问题的能
力, 会用不等式的基本性质解简单的不等式.(重点、
难点)
学习目标
新课导入
前面我们已经学习过等式的基本性质
(1)等式的两边都加上(或都减去)同一个
数或同一个整式,等式仍然成立.
(2)等式的两边都乘以(或除以)一个不为0
的数,等式仍然成立.
猜想 :不等式也具有同样的性质吗?
复习引入
新课讲解
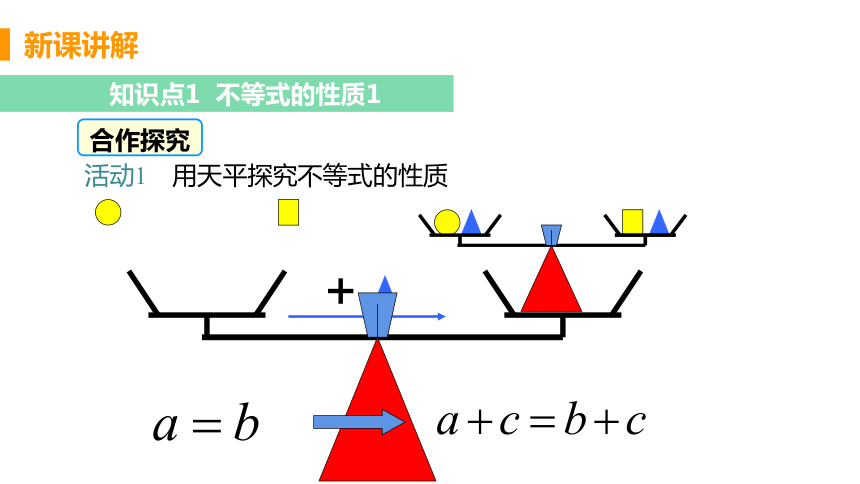
知识点1 不等式的性质1
+
合作探究
活动1 用天平探究不等式的性质
新课讲解
问题2 一辆轿车在一条规定车速应高于60km/h,且低于100 km/h的高速公路上行驶,如何用式子来表示轿车在该高速公路上行驶的路程s(km)与行驶时间x(h)之间的关系呢?
根据路程与速度、时间之间的关系可得: s>60x,且s<100x.
新课讲解
a
b
b+2
a+2
a b
a+2 b+2
a
b
b-c
a-c
a < b
a-c b-c
<
<
<
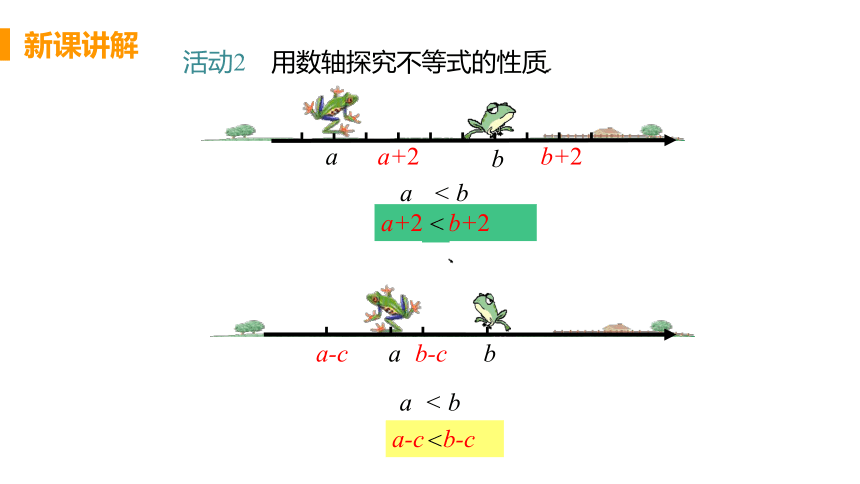
活动2 用数轴探究不等式的性质
新课讲解
解: 因为 a>b,两边都加上3,
因为 a 由不等式基本性质1,得
a+3 > b+3;
由不等式基本性质1,得
a-5 < b-5 .
(1)已知 a>b,则a+3 b+3
(2)已知 a>
<
例1 用“>”或“<”填空:
典例精析
新课讲解
用“>”或“<”填空,并说明是根据不等式的哪一条性质:
(1)若x+3>6,则x______3,
根据______________;
(2)若a-2<3,则a______5,
根据____________.
练一练
>
<
不等式性质1
不等式性质1
新课讲解
知识点2 不等式的基本性质2、3
问题1 已知苹果的价格是a元/kg,梨的价格是b元/kg,且a > b. 小李各买了3kg苹果和梨,则买哪种水果花钱较多?
用不等号填空: 3a 3b.
问题2 在某次知识抢答赛中,甲、乙两队的总得分分别为a,b,其中a>b. 已知每队人员均为3名,则哪队的平均得分高?
用不等号填空:
a÷3 b÷3.
>
>
新课讲解
用不等号填一填:
1.a b ;
2.2a 2b;
3. .
如图所示,托盘天平的右盘放上一质量为bg的立体木块,左盘放上一质量为ag的立体木块,天平向左倾斜.
合作与交流
ag
bg
>
>
>
ag
bg
你发现了什么?
新课讲解
不等式基本性质2 不等式的两边都乘(或除以)同一个正数,不等号的方向不变.
即,如果a > b,c > 0,那么 ac > bc , > .
总结归纳
新课讲解
合作与交流
a>b
-a-b
a-a-b>b-a-b
-b>-a
(-1)×a<(-1)×b
×(-1)
不等式两边同乘-1,不等号方向改变.
猜想:不等式两边同乘一个负数,不等号方向改变.
a>b
×(-1)
-a<-b
×3
-3a<-3b
×c(c>0)
-ac<-bc
×-c(-c<0)
新课讲解
不等式基本性质3 不等式的两边都乘(或除以)同一个负数,不等号的方向改变.
即,如果a > b,c < 0,那么 ac < bc , < .
总结归纳
新课讲解
因为 a>b,两边都乘3,
因为 a>b,两边都乘-1,
解:
由不等式基本性质2,得
3a > 3b.
由不等式基本性质3,得
-a < -b.
(1)已知 a>b,则3a 3b ;
(2)已知 a>b,则-a -b .
>
<
例2 用“>”或“<”填空:
新课讲解
因为 a 由不等式基本性质3,得
由不等式基本性质1,得
(3)已知 a >
因为 ,两边都加上2,
新课讲解
1.设a>b,用“<”“>”填空并回答是根据不等式的哪一条基本性质.
(1) a - 7____b - 7;
(2) a÷6____b÷6
(3) 0.1a____0.1b;
(4) -4a____-4b
(5) 2a+3____2b+3;
(6)(m2+1)a____ (m2+1)b(m为常数).
>
>
>
>
>
<
不等式的性质1
不等式的性质2
不等式的性质2
不等式的性质3
不等式的性质1,2
不等式的性质2
练一练
新课讲解
2.已知a<0,用“<”“>”填空:
(1)a+2 ____2; ?(2)a-1 _____-1;
(3)3a______0; (4) ______0;
(5)a2_____0; (6)a3______0;
(7)a-1_____0;??(8)|a|______0.
<
<
<
>
<
>
<
>
新课讲解
思考: 等式有对称性及传递性,那么不等式具有对称性和传递性吗?
已知x>5,那么5由8如:8<10,10<15 ,8 15.
x>5 5<
性质4(对称性):如果a>b,那么b性质5(同向传递性):如果a>b,b>c,那么a>c.
新课讲解
例3 如果不等式 (a+1)x<a+1可变形为 x>1,那么a 必须满足________.
方法总结:只有当不等式的两边都乘(或除以)一个负数时,不等号的方向才改变.
解析:根据不等式的基本性质可判断,a+1为负数,即a+1<0,可得 a<-1.
a<-1
新课讲解
知识点3 利用不等式的性质解简单的不等式
例4 利用不等式的性质解下列不等式:
(1) x-7>26; (2) 3x<2x+1;
(3) >50; (4) -4x>3.
解未知数为x的不等式
化为x>a或x﹤a的形式
目标
方法:不等式基本性质1~3
思路:
新课讲解
解 (1)为了使不等式x-7>26中不等号的一边变为x,
根据不等式的性质1,不等式两边都加7,不
等号的方向不变,得 x-7+7﹥26+7,即x﹥33.
这个不等式的解集在数轴上的表示如图所示:
0
33
(1) x-7>26;
新课讲解
(2)为了使不等式3x<2x+1中不等号的一边变为x,根
据_____________,不等式两边都减去____,不等
号的方向_____,得 .
3x-2x﹤2x+1-2x ,即 x﹤1
这个不等式的解集在数轴上的表示如图所示:
0
1
不等式性质1
2x
不变
(2) 3x<2x+1;
新课讲解
(3)为了使不等式 ﹥50中不等号的一边变为x,根据
不等式的性质2,不等式的两边都除以 ,不等号
的方向不变,得
x﹥75.
这个不等式的解集在数轴上的表示如图所示:
0
75
(3) >50;
新课讲解
(4)为了使不等式-4x﹥3中的不等号的一边变为x,
根据______________,不等式两边都除以____,
不等号的方向______,得
x﹤- .
这个不等式的解集在数轴上的表示如图所示:
-
4
3
0
不等式的性质3
-4
改变
(4) -4x>3.
课堂小结
不等式的基本性质
不等式的基本性质2
不等式的基本性质3
→
→
如果 那么
如果 那么
应用性质对不等式简单变形
不等式的基本性质1
如果a>b,那么a+c>b+c,
a-c>b-c
→
当堂小练
1. 已知a < b,用“>”或“<”填空:
(1)a +12 b +12 ;
(2)b-10 a -10 .
<
>
解:x < 2
解:x < 6
2. 把下列不等式化为x>a或x(1)5>3+x;
(2)2x<x+6.
拓展与延伸
3.利用不等式的性质解下列不等式,并在数轴上表示其解集:
(2)-2x > 3;
(1)x-5 > -1;
(3)7x < 6x-6.
x>4
x<-6
4
0
0
0
-6
布置作业
请完成对应习题
9.1 不等式
9.1.2 不等式的性质
1.理解并掌握不等式的基本性质;
2.通过实例操作,培养学生观察、分析、比较问题的能
力, 会用不等式的基本性质解简单的不等式.(重点、
难点)
学习目标
新课导入
前面我们已经学习过等式的基本性质
(1)等式的两边都加上(或都减去)同一个
数或同一个整式,等式仍然成立.
(2)等式的两边都乘以(或除以)一个不为0
的数,等式仍然成立.
猜想 :不等式也具有同样的性质吗?
复习引入
新课讲解
知识点1 不等式的性质1
+
合作探究
活动1 用天平探究不等式的性质
新课讲解
问题2 一辆轿车在一条规定车速应高于60km/h,且低于100 km/h的高速公路上行驶,如何用式子来表示轿车在该高速公路上行驶的路程s(km)与行驶时间x(h)之间的关系呢?
根据路程与速度、时间之间的关系可得: s>60x,且s<100x.
新课讲解
a
b
b+2
a+2
a b
a+2 b+2
a
b
b-c
a-c
a < b
a-c b-c
<
<
<
活动2 用数轴探究不等式的性质
新课讲解
解: 因为 a>b,两边都加上3,
因为 a
a+3 > b+3;
由不等式基本性质1,得
a-5 < b-5 .
(1)已知 a>b,则a+3 b+3
(2)已知 a
<
例1 用“>”或“<”填空:
典例精析
新课讲解
用“>”或“<”填空,并说明是根据不等式的哪一条性质:
(1)若x+3>6,则x______3,
根据______________;
(2)若a-2<3,则a______5,
根据____________.
练一练
>
<
不等式性质1
不等式性质1
新课讲解
知识点2 不等式的基本性质2、3
问题1 已知苹果的价格是a元/kg,梨的价格是b元/kg,且a > b. 小李各买了3kg苹果和梨,则买哪种水果花钱较多?
用不等号填空: 3a 3b.
问题2 在某次知识抢答赛中,甲、乙两队的总得分分别为a,b,其中a>b. 已知每队人员均为3名,则哪队的平均得分高?
用不等号填空:
a÷3 b÷3.
>
>
新课讲解
用不等号填一填:
1.a b ;
2.2a 2b;
3. .
如图所示,托盘天平的右盘放上一质量为bg的立体木块,左盘放上一质量为ag的立体木块,天平向左倾斜.
合作与交流
ag
bg
>
>
>
ag
bg
你发现了什么?
新课讲解
不等式基本性质2 不等式的两边都乘(或除以)同一个正数,不等号的方向不变.
即,如果a > b,c > 0,那么 ac > bc , > .
总结归纳
新课讲解
合作与交流
a>b
-a-b
a-a-b>b-a-b
-b>-a
(-1)×a<(-1)×b
×(-1)
不等式两边同乘-1,不等号方向改变.
猜想:不等式两边同乘一个负数,不等号方向改变.
a>b
×(-1)
-a<-b
×3
-3a<-3b
×c(c>0)
-ac<-bc
×-c(-c<0)
新课讲解
不等式基本性质3 不等式的两边都乘(或除以)同一个负数,不等号的方向改变.
即,如果a > b,c < 0,那么 ac < bc , < .
总结归纳
新课讲解
因为 a>b,两边都乘3,
因为 a>b,两边都乘-1,
解:
由不等式基本性质2,得
3a > 3b.
由不等式基本性质3,得
-a < -b.
(1)已知 a>b,则3a 3b ;
(2)已知 a>b,则-a -b .
>
<
例2 用“>”或“<”填空:
新课讲解
因为 a
由不等式基本性质1,得
(3)已知 a
因为 ,两边都加上2,
新课讲解
1.设a>b,用“<”“>”填空并回答是根据不等式的哪一条基本性质.
(1) a - 7____b - 7;
(2) a÷6____b÷6
(3) 0.1a____0.1b;
(4) -4a____-4b
(5) 2a+3____2b+3;
(6)(m2+1)a____ (m2+1)b(m为常数).
>
>
>
>
>
<
不等式的性质1
不等式的性质2
不等式的性质2
不等式的性质3
不等式的性质1,2
不等式的性质2
练一练
新课讲解
2.已知a<0,用“<”“>”填空:
(1)a+2 ____2; ?(2)a-1 _____-1;
(3)3a______0; (4) ______0;
(5)a2_____0; (6)a3______0;
(7)a-1_____0;??(8)|a|______0.
<
<
<
>
<
>
<
>
新课讲解
思考: 等式有对称性及传递性,那么不等式具有对称性和传递性吗?
已知x>5,那么5
x>5 5
性质4(对称性):如果a>b,那么b
新课讲解
例3 如果不等式 (a+1)x<a+1可变形为 x>1,那么a 必须满足________.
方法总结:只有当不等式的两边都乘(或除以)一个负数时,不等号的方向才改变.
解析:根据不等式的基本性质可判断,a+1为负数,即a+1<0,可得 a<-1.
a<-1
新课讲解
知识点3 利用不等式的性质解简单的不等式
例4 利用不等式的性质解下列不等式:
(1) x-7>26; (2) 3x<2x+1;
(3) >50; (4) -4x>3.
解未知数为x的不等式
化为x>a或x﹤a的形式
目标
方法:不等式基本性质1~3
思路:
新课讲解
解 (1)为了使不等式x-7>26中不等号的一边变为x,
根据不等式的性质1,不等式两边都加7,不
等号的方向不变,得 x-7+7﹥26+7,即x﹥33.
这个不等式的解集在数轴上的表示如图所示:
0
33
(1) x-7>26;
新课讲解
(2)为了使不等式3x<2x+1中不等号的一边变为x,根
据_____________,不等式两边都减去____,不等
号的方向_____,得 .
3x-2x﹤2x+1-2x ,即 x﹤1
这个不等式的解集在数轴上的表示如图所示:
0
1
不等式性质1
2x
不变
(2) 3x<2x+1;
新课讲解
(3)为了使不等式 ﹥50中不等号的一边变为x,根据
不等式的性质2,不等式的两边都除以 ,不等号
的方向不变,得
x﹥75.
这个不等式的解集在数轴上的表示如图所示:
0
75
(3) >50;
新课讲解
(4)为了使不等式-4x﹥3中的不等号的一边变为x,
根据______________,不等式两边都除以____,
不等号的方向______,得
x﹤- .
这个不等式的解集在数轴上的表示如图所示:
-
4
3
0
不等式的性质3
-4
改变
(4) -4x>3.
课堂小结
不等式的基本性质
不等式的基本性质2
不等式的基本性质3
→
→
如果 那么
如果 那么
应用性质对不等式简单变形
不等式的基本性质1
如果a>b,那么a+c>b+c,
a-c>b-c
→
当堂小练
1. 已知a < b,用“>”或“<”填空:
(1)a +12 b +12 ;
(2)b-10 a -10 .
<
>
解:x < 2
解:x < 6
2. 把下列不等式化为x>a或x
(2)2x<x+6.
拓展与延伸
3.利用不等式的性质解下列不等式,并在数轴上表示其解集:
(2)-2x > 3;
(1)x-5 > -1;
(3)7x < 6x-6.
x>4
x<-6
4
0
0
0
-6
布置作业
请完成对应习题
