人教版七年级数学下册知识双清练:5.1.1 相交线(Word版含答案)
文档属性
| 名称 | 人教版七年级数学下册知识双清练:5.1.1 相交线(Word版含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 182.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-18 10:24:22 | ||
图片预览


文档简介
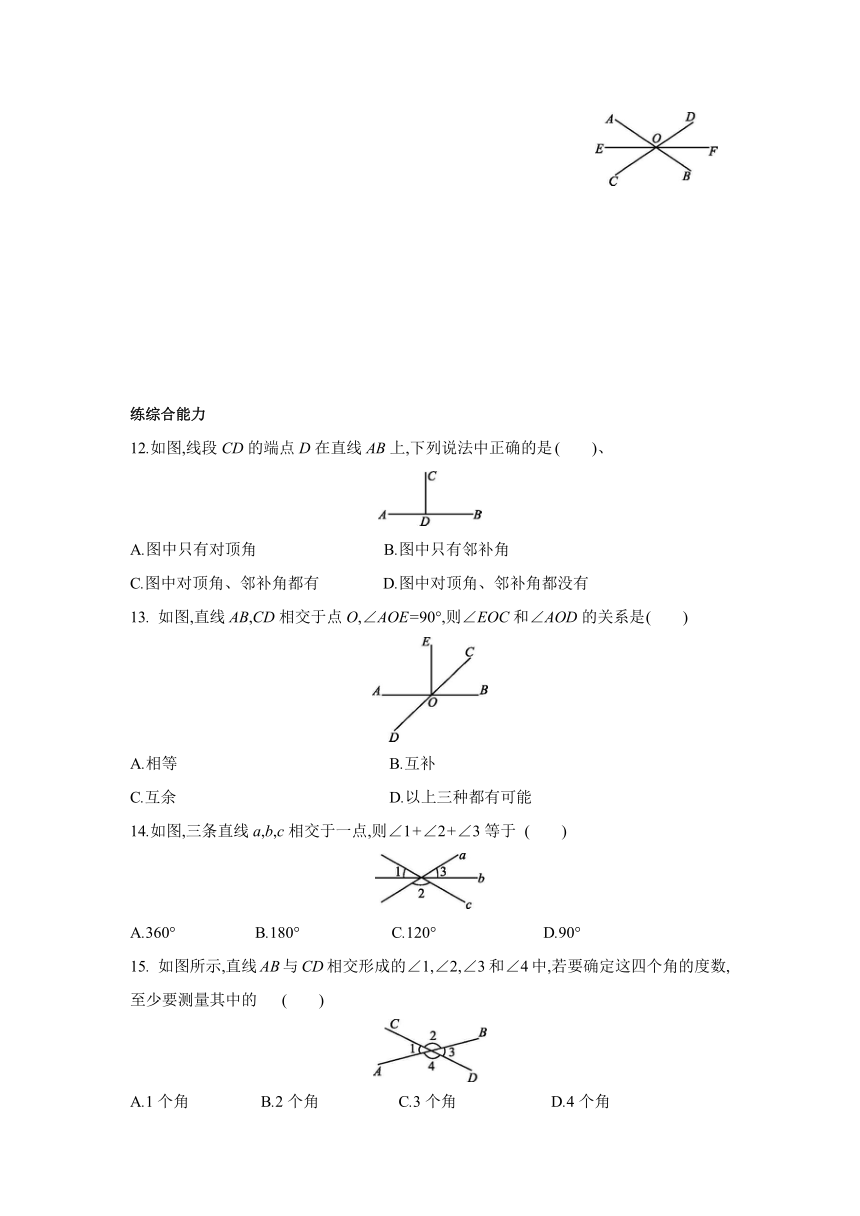
5.1.1 相交线
练知识点
知识点
1 邻补角的定义及性质
1.如图,∠1的邻补角是
( )
A.∠2
B.∠3
C.∠2或∠3
D.∠4
2.下列关于邻补角的说法,正确的是
( )
A.和为180°的两个角互为邻补角
B.有公共顶点且互补的两个角互为邻补角
C.有一条公共边且互补的两个角互为邻补角
D.有一条公共边,另一边互为反向延长线的两个角互为邻补角
3.如图,直线a,b相交于点O,若∠1=36°,则∠2的度数为
( )
A.54°
B.64°
C.144°
D.154°
4.如图,直线AB,CD相交于点O,OE平分∠AOC,若∠1=30°,则∠AOD= .
知识点
2 对顶角的定义及性质
5.
下列各图中,∠1与∠2是对顶角的是
( )
6.下列说法中正确的是
( )
A.相等的两个角互为对顶角
B.有公共顶点且相等的两个角互为对顶角
C.两直线相交所成的角互为对顶角
D.有公共顶点且两边互为反向延长线的两个角互为对顶角
7.如图,直线a,b相交于点O,因为∠1+∠2=180°,∠3+∠2=180°,所以∠1=∠3,这是根据
( )
A.同角的余角相等
B.等角的余角相等
C.同角的补角相等
D.等角的补角相等
8.
如图,要测量两堵围墙形成的∠AOB的度数,先分别延长AO,BO得到∠COD,然后通过测量∠COD的度数得到∠AOB的度数,其中运用的原理是
( )
A.对顶角相等
B.同角的余角相等
C.等角的余角相等
D.两直线相交,只有一个交点
9.用剪刀剪东西时,剪刀张开的角度如图所示,当∠AOB增大25°时,∠COD增大 .?
10.如图,直线AB,CD相交于点O,射线OM平分∠AOC,∠AOM=36°,则
∠BOD= .?
11.如图,三条直线AB,CD,EF相交于一点O,且OF平分∠BOD,则OE是不是∠AOC的平分线?为什么?
练综合能力
12.如图,线段CD的端点D在直线AB上,下列说法中正确的是
( )、
A.图中只有对顶角
B.图中只有邻补角
C.图中对顶角、邻补角都有
D.图中对顶角、邻补角都没有
13.
如图,直线AB,CD相交于点O,∠AOE=90°,则∠EOC和∠AOD的关系是
( )
A.相等
B.互补
C.互余
D.以上三种都有可能
14.如图,三条直线a,b,c相交于一点,则∠1+∠2+∠3等于
( )
A.360°
B.180°
C.120°
D.90°
15.
如图所示,直线AB与CD相交形成的∠1,∠2,∠3和∠4中,若要确定这四个角的度数,至少要测量其中的
( )
A.1个角
B.2个角
C.3个角
D.4个角
16.如图,直线AB,CD相交于点O,若∠AOC+∠BOD=100°,则∠AOD= .?
17.如图,直线AB,CD相交于点O,OE平分∠AOD.若∠BOD=110°,则
∠AOE= °.?
18.如图,直线AB,CD相交于点O,已知∠AOC=75°,∠BOE∶∠DOE=2∶3.
(1)求∠BOE的度数;
(2)若OF平分∠AOE,则∠AOC与∠AOF相等吗?为什么?
19.观察图中的各个图形,寻找对顶角(不含平角):
(1)如图①所示,两条直线AB与CD相交于一点形成 对对顶角;?
(2)如图②所示,三条直线AB,CD,EF相交于一点形成 对对顶角;?
(3)如图③所示,四条直线AB,CD,EF,GH相交于一点形成 对对顶角;?
(4)探究(1)~(3)各题中直线条数与对顶角对数之间的关系,若有n(n≥2且n为整数)条直线相交于一点,则可形成 对对顶角;?
(5)根据(4)中探究得到的结论计算:若有2021条直线相交于一点,则可形成 对对顶角.?
参考答案
1.A 2.D
3.C 解析:
因为∠1+∠2=180°,∠1=36°,所以∠2=144°.
4.120° 解析:
因为OE平分∠AOC,∠1=30°,所以∠AOC=2∠1=60°,所以∠AOD=180°-∠AOC=120°.
5.A
6.D 解析:
举反例是解决概念性问题的基本方法,如图,∠AOB和∠COD有公共顶点且大小相等,但它们不是对顶角,故选项A,B都错.两直线相交所成的角中既有对顶角,又有邻补角,故选项C错.
7.C 解析:
因为∠1与∠3都是∠2的补角,所以∠1=∠3(同角的补角相等).
8.A 解析:
延长AO到点C,延长BO到点D,然后测量∠COD的度数,根据对顶角相等可得∠AOB=∠COD.故其中运用的原理是对顶角相等.
9.25° 解析:
因为∠AOB与∠COD是对顶角,所以当剪子口∠AOB增大25°时,∠COD也增大25°.
10.72° 解析:
因为射线OM平分∠AOC,所以∠AOC=2∠AOM=72°,所以∠BOD=∠AOC=72°.
11.解:OE是∠AOC的平分线.理由如下:
因为OF平分∠BOD,
所以∠BOF=∠DOF.
又因为∠BOF=∠AOE,∠DOF=∠COE,
所以∠AOE=∠COE,
所以OE是∠AOC的平分线.
12.B
13.C 解析:
因为∠AOE=90°,
所以∠EOB=90°,
所以∠EOC+∠BOC=90°.
因为∠BOC=∠AOD,所以∠EOC+∠AOD=90°,即∠EOC和∠AOD互余.
14.B
15.A 解析:
根据题意可得∠1=∠3,∠2=∠4,且∠1+∠2=∠3+∠4=180°,
所以要确定这四个角的度数,至少要测量其中的1个角即可.
16.130° 解析:
因为∠AOC与∠BOD是对顶角,
所以∠AOC=∠BOD.
又因为∠AOC+∠BOD=100°,
所以∠AOC=50°.
因为∠AOC+∠AOD=180°,
所以∠AOD=180°-∠AOC=130°.
17.35
18.解:(1)设∠BOE=2x,则∠DOE=3x.
因为∠BOE+∠DOE=∠BOD=∠AOC=75°,
所以2x+3x=75°,
解得x=15°,
所以2x=30°,3x=45°,
所以∠BOE=30°.
(2)∠AOC=∠AOF.理由如下:
因为∠BOE=30°,所以∠AOE=150°.
因为OF平分∠AOE,所以∠AOF=75°,
所以∠AOC=∠AOF.
19.(1)2 (2)6 (3)12
(4)n(n-1) (5)4082420
练知识点
知识点
1 邻补角的定义及性质
1.如图,∠1的邻补角是
( )
A.∠2
B.∠3
C.∠2或∠3
D.∠4
2.下列关于邻补角的说法,正确的是
( )
A.和为180°的两个角互为邻补角
B.有公共顶点且互补的两个角互为邻补角
C.有一条公共边且互补的两个角互为邻补角
D.有一条公共边,另一边互为反向延长线的两个角互为邻补角
3.如图,直线a,b相交于点O,若∠1=36°,则∠2的度数为
( )
A.54°
B.64°
C.144°
D.154°
4.如图,直线AB,CD相交于点O,OE平分∠AOC,若∠1=30°,则∠AOD= .
知识点
2 对顶角的定义及性质
5.
下列各图中,∠1与∠2是对顶角的是
( )
6.下列说法中正确的是
( )
A.相等的两个角互为对顶角
B.有公共顶点且相等的两个角互为对顶角
C.两直线相交所成的角互为对顶角
D.有公共顶点且两边互为反向延长线的两个角互为对顶角
7.如图,直线a,b相交于点O,因为∠1+∠2=180°,∠3+∠2=180°,所以∠1=∠3,这是根据
( )
A.同角的余角相等
B.等角的余角相等
C.同角的补角相等
D.等角的补角相等
8.
如图,要测量两堵围墙形成的∠AOB的度数,先分别延长AO,BO得到∠COD,然后通过测量∠COD的度数得到∠AOB的度数,其中运用的原理是
( )
A.对顶角相等
B.同角的余角相等
C.等角的余角相等
D.两直线相交,只有一个交点
9.用剪刀剪东西时,剪刀张开的角度如图所示,当∠AOB增大25°时,∠COD增大 .?
10.如图,直线AB,CD相交于点O,射线OM平分∠AOC,∠AOM=36°,则
∠BOD= .?
11.如图,三条直线AB,CD,EF相交于一点O,且OF平分∠BOD,则OE是不是∠AOC的平分线?为什么?
练综合能力
12.如图,线段CD的端点D在直线AB上,下列说法中正确的是
( )、
A.图中只有对顶角
B.图中只有邻补角
C.图中对顶角、邻补角都有
D.图中对顶角、邻补角都没有
13.
如图,直线AB,CD相交于点O,∠AOE=90°,则∠EOC和∠AOD的关系是
( )
A.相等
B.互补
C.互余
D.以上三种都有可能
14.如图,三条直线a,b,c相交于一点,则∠1+∠2+∠3等于
( )
A.360°
B.180°
C.120°
D.90°
15.
如图所示,直线AB与CD相交形成的∠1,∠2,∠3和∠4中,若要确定这四个角的度数,至少要测量其中的
( )
A.1个角
B.2个角
C.3个角
D.4个角
16.如图,直线AB,CD相交于点O,若∠AOC+∠BOD=100°,则∠AOD= .?
17.如图,直线AB,CD相交于点O,OE平分∠AOD.若∠BOD=110°,则
∠AOE= °.?
18.如图,直线AB,CD相交于点O,已知∠AOC=75°,∠BOE∶∠DOE=2∶3.
(1)求∠BOE的度数;
(2)若OF平分∠AOE,则∠AOC与∠AOF相等吗?为什么?
19.观察图中的各个图形,寻找对顶角(不含平角):
(1)如图①所示,两条直线AB与CD相交于一点形成 对对顶角;?
(2)如图②所示,三条直线AB,CD,EF相交于一点形成 对对顶角;?
(3)如图③所示,四条直线AB,CD,EF,GH相交于一点形成 对对顶角;?
(4)探究(1)~(3)各题中直线条数与对顶角对数之间的关系,若有n(n≥2且n为整数)条直线相交于一点,则可形成 对对顶角;?
(5)根据(4)中探究得到的结论计算:若有2021条直线相交于一点,则可形成 对对顶角.?
参考答案
1.A 2.D
3.C 解析:
因为∠1+∠2=180°,∠1=36°,所以∠2=144°.
4.120° 解析:
因为OE平分∠AOC,∠1=30°,所以∠AOC=2∠1=60°,所以∠AOD=180°-∠AOC=120°.
5.A
6.D 解析:
举反例是解决概念性问题的基本方法,如图,∠AOB和∠COD有公共顶点且大小相等,但它们不是对顶角,故选项A,B都错.两直线相交所成的角中既有对顶角,又有邻补角,故选项C错.
7.C 解析:
因为∠1与∠3都是∠2的补角,所以∠1=∠3(同角的补角相等).
8.A 解析:
延长AO到点C,延长BO到点D,然后测量∠COD的度数,根据对顶角相等可得∠AOB=∠COD.故其中运用的原理是对顶角相等.
9.25° 解析:
因为∠AOB与∠COD是对顶角,所以当剪子口∠AOB增大25°时,∠COD也增大25°.
10.72° 解析:
因为射线OM平分∠AOC,所以∠AOC=2∠AOM=72°,所以∠BOD=∠AOC=72°.
11.解:OE是∠AOC的平分线.理由如下:
因为OF平分∠BOD,
所以∠BOF=∠DOF.
又因为∠BOF=∠AOE,∠DOF=∠COE,
所以∠AOE=∠COE,
所以OE是∠AOC的平分线.
12.B
13.C 解析:
因为∠AOE=90°,
所以∠EOB=90°,
所以∠EOC+∠BOC=90°.
因为∠BOC=∠AOD,所以∠EOC+∠AOD=90°,即∠EOC和∠AOD互余.
14.B
15.A 解析:
根据题意可得∠1=∠3,∠2=∠4,且∠1+∠2=∠3+∠4=180°,
所以要确定这四个角的度数,至少要测量其中的1个角即可.
16.130° 解析:
因为∠AOC与∠BOD是对顶角,
所以∠AOC=∠BOD.
又因为∠AOC+∠BOD=100°,
所以∠AOC=50°.
因为∠AOC+∠AOD=180°,
所以∠AOD=180°-∠AOC=130°.
17.35
18.解:(1)设∠BOE=2x,则∠DOE=3x.
因为∠BOE+∠DOE=∠BOD=∠AOC=75°,
所以2x+3x=75°,
解得x=15°,
所以2x=30°,3x=45°,
所以∠BOE=30°.
(2)∠AOC=∠AOF.理由如下:
因为∠BOE=30°,所以∠AOE=150°.
因为OF平分∠AOE,所以∠AOF=75°,
所以∠AOC=∠AOF.
19.(1)2 (2)6 (3)12
(4)n(n-1) (5)4082420
