人教版数学七年级下册 9.3.1 一元一次不等式组及其解法 课件(21张)
文档属性
| 名称 | 人教版数学七年级下册 9.3.1 一元一次不等式组及其解法 课件(21张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-17 00:00:00 | ||
图片预览








文档简介
第九章 不等式与不等式组
9.3 一元一次不等式组
课时1 一元一次不等式组及其解法
1.通过具体操作,在解一元一次不等式组的过程中形成正确的解不等式组的思路与方法;(重点、难点)
2.掌握在数轴上正确表示一元一次不等式组的解集的方法.
学习目标
新课导入
嗨,我听管理员说,这头大象的体重不足5吨呢!
同学们,你能根据上图对话片断估计出这头大象的体重范围吗?请说说你的理由!
看,这头大象好大呀,体重肯定不少于3吨!
若设大象的体重为x吨,请用不等式的知识分别表示上面两位同学谈话的内容:
x≥3 ①
x<5 ②
情境引入
新课讲解
知识点1 一元一次不等式组的概念及解集
问题:一个长方形足球场的宽为70m,如果它的周长大于350m,面积小于7630m2,求这个足球场的长的取值范围,并判断这个足球场是否可以进行国际足球比赛(注:用于国际足球比赛的足球场的长在100至110m之间,宽在64至75m之间).
新课讲解
如果设足球场的长为x m,那么它的周长就是2(x+70)m,面积为70x m2.
根据已知条件,我们知道x的取值范围要使
2(x+70)>350 和70x<7630
这两个不等式同时成立.
新课讲解
为此,我们用大括号把上述两个不等式联立起来,得
2(x+70)>350 和70x<7630
像 这样,关于同一未知数的两个一元一次不等式合在一起,就组成一个一元一次不等式组.
新课讲解
练一练
判断下列不等式组是否为一元一次不等式组:
×
×
√
√
新课讲解
思考:怎样确定上面的不等式组中未知数的取值范围呢?
类比方程组的求解,不等式组中的各个不等式解集的公共部分,就是不等式组中的未知数的取值范围.
归纳:我们把几个一元一次不等式解集的公共部分,叫做由它们所组成的一元一次不等式组的解集.
求不等式组的解集的过程,叫做解不等式组.
新课讲解
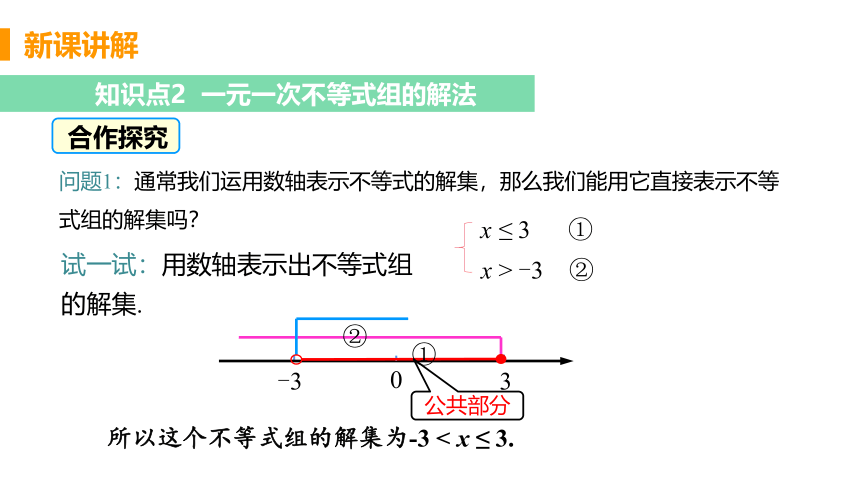
知识点2 一元一次不等式组的解法
问题1:通常我们运用数轴表示不等式的解集,那么我们能用它直接表示不等式组的解集吗?
试一试:用数轴表示出不等式组 的解集.
所以这个不等式组的解集为-3 < x ≤ 3.
x > -3 ②
x ≤ 3 ①
0
-3
3
公共部分
①
②
合作探究
新课讲解
问题2:解由两个一元一次不等式组成的不等式组,在取各不等式的解的公共部分时,有几种不同情况?
a b
a b
a b
a b
同大取大
同小取小
大小小大中间找
大大小小无处找
x>b
xa无解
新课讲解
填表:
不等式组
不等式组的解集
x﹥-3
-5﹤x≤-3
x<-3
无解
练一练
新课讲解
试一试:解上面问题中的不等式组
解:解不等式①,得
解不等式②,得
①
②
x>105.
x<109.
新课讲解
的解集就是
x> 105与x<109的公共部分.
不等式组
0
105
109
由图容易发现它们的公共部分是105<x <109,这就是由不等式①、②组成的不等式组
的解集.
新课讲解
解不等式②,得
x <-3.
例1 解不等式组:
解: 解不等式①,得
x ≤ 3.
①
②
把不等式①、②的解集在数轴上表示出来,如图:
0
-3
3
由图可知,不等式①、②的解集的公共部分就是
x<-3,所以这个不等式组的解集是 x<-3.
典例精析
新课讲解
例2 解不等式组:
①
②
解: 解不等式①,得
x >-2.
解不等式②,得
x >6.
把不等式①、②的解集在数轴上表示出来,
如图:
0
-2
6
由图可知,不等式①、②的解集的公共部分就是x>6,所以这个不等式组的解集是x>6.
课堂小结
一元一次不等式组
一元一次不等式组的概念
↓
利用公共部分确定不等式组的解集
在数轴上分别表示各个不等式的解集
解每个不等式
↓
一元一次不等式组的解集在数轴上的表示
一元一次不等式组的解集
解一元一次不等式组
→
↓
当堂小练
解不等式②,得
x <6.
1. 解不等式组:
解: 解不等式①,得
①
②
把不等式①、②的解集在数轴上表示出来,
如图:
3
0
6
因此,原不等式组的解集为
当堂小练
解不等式②,得
x >4.
2. 解不等式组:
解: 解不等式①,得
x >2.
①
②
把不等式①、②的解集在数轴上表示出来,如图:
2
0
4
由图可知,不等式①、②的解集的公共部分就是x >4,所以这个不等式组的解集是x >4.
拓展与延伸
3. x取哪些整数值时,不等式2-x≥0与
都成立?
解:由题意可得不等式组
解不等式①,得x≤2,
解不等式②,得x>-3.
故此不等式组的解集为-3<x≤2,x可取的整数值为-2,-1,0,1,2.
①
②
拓展与延伸
解:①×2+②得:5x=10m-5,得:x=2m-1.
①-②×2得:5y=5m+40,得:y=m+8.
又∵x,y的值都是正数,且x∴
解得∴m的取值范围为 <m<9.
2m-1>0
m+8>0
2m-14.已知方程组
的解x,y的值都是正数,且x2x+y=5m+6 ①
x-2y=-17 ②
布置作业
请完成对应习题
9.3 一元一次不等式组
课时1 一元一次不等式组及其解法
1.通过具体操作,在解一元一次不等式组的过程中形成正确的解不等式组的思路与方法;(重点、难点)
2.掌握在数轴上正确表示一元一次不等式组的解集的方法.
学习目标
新课导入
嗨,我听管理员说,这头大象的体重不足5吨呢!
同学们,你能根据上图对话片断估计出这头大象的体重范围吗?请说说你的理由!
看,这头大象好大呀,体重肯定不少于3吨!
若设大象的体重为x吨,请用不等式的知识分别表示上面两位同学谈话的内容:
x≥3 ①
x<5 ②
情境引入
新课讲解
知识点1 一元一次不等式组的概念及解集
问题:一个长方形足球场的宽为70m,如果它的周长大于350m,面积小于7630m2,求这个足球场的长的取值范围,并判断这个足球场是否可以进行国际足球比赛(注:用于国际足球比赛的足球场的长在100至110m之间,宽在64至75m之间).
新课讲解
如果设足球场的长为x m,那么它的周长就是2(x+70)m,面积为70x m2.
根据已知条件,我们知道x的取值范围要使
2(x+70)>350 和70x<7630
这两个不等式同时成立.
新课讲解
为此,我们用大括号把上述两个不等式联立起来,得
2(x+70)>350 和70x<7630
像 这样,关于同一未知数的两个一元一次不等式合在一起,就组成一个一元一次不等式组.
新课讲解
练一练
判断下列不等式组是否为一元一次不等式组:
×
×
√
√
新课讲解
思考:怎样确定上面的不等式组中未知数的取值范围呢?
类比方程组的求解,不等式组中的各个不等式解集的公共部分,就是不等式组中的未知数的取值范围.
归纳:我们把几个一元一次不等式解集的公共部分,叫做由它们所组成的一元一次不等式组的解集.
求不等式组的解集的过程,叫做解不等式组.
新课讲解
知识点2 一元一次不等式组的解法
问题1:通常我们运用数轴表示不等式的解集,那么我们能用它直接表示不等式组的解集吗?
试一试:用数轴表示出不等式组 的解集.
所以这个不等式组的解集为-3 < x ≤ 3.
x > -3 ②
x ≤ 3 ①
0
-3
3
公共部分
①
②
合作探究
新课讲解
问题2:解由两个一元一次不等式组成的不等式组,在取各不等式的解的公共部分时,有几种不同情况?
a b
a b
a b
a b
同大取大
同小取小
大小小大中间找
大大小小无处找
x>b
xa
新课讲解
填表:
不等式组
不等式组的解集
x﹥-3
-5﹤x≤-3
x<-3
无解
练一练
新课讲解
试一试:解上面问题中的不等式组
解:解不等式①,得
解不等式②,得
①
②
x>105.
x<109.
新课讲解
的解集就是
x> 105与x<109的公共部分.
不等式组
0
105
109
由图容易发现它们的公共部分是105<x <109,这就是由不等式①、②组成的不等式组
的解集.
新课讲解
解不等式②,得
x <-3.
例1 解不等式组:
解: 解不等式①,得
x ≤ 3.
①
②
把不等式①、②的解集在数轴上表示出来,如图:
0
-3
3
由图可知,不等式①、②的解集的公共部分就是
x<-3,所以这个不等式组的解集是 x<-3.
典例精析
新课讲解
例2 解不等式组:
①
②
解: 解不等式①,得
x >-2.
解不等式②,得
x >6.
把不等式①、②的解集在数轴上表示出来,
如图:
0
-2
6
由图可知,不等式①、②的解集的公共部分就是x>6,所以这个不等式组的解集是x>6.
课堂小结
一元一次不等式组
一元一次不等式组的概念
↓
利用公共部分确定不等式组的解集
在数轴上分别表示各个不等式的解集
解每个不等式
↓
一元一次不等式组的解集在数轴上的表示
一元一次不等式组的解集
解一元一次不等式组
→
↓
当堂小练
解不等式②,得
x <6.
1. 解不等式组:
解: 解不等式①,得
①
②
把不等式①、②的解集在数轴上表示出来,
如图:
3
0
6
因此,原不等式组的解集为
当堂小练
解不等式②,得
x >4.
2. 解不等式组:
解: 解不等式①,得
x >2.
①
②
把不等式①、②的解集在数轴上表示出来,如图:
2
0
4
由图可知,不等式①、②的解集的公共部分就是x >4,所以这个不等式组的解集是x >4.
拓展与延伸
3. x取哪些整数值时,不等式2-x≥0与
都成立?
解:由题意可得不等式组
解不等式①,得x≤2,
解不等式②,得x>-3.
故此不等式组的解集为-3<x≤2,x可取的整数值为-2,-1,0,1,2.
①
②
拓展与延伸
解:①×2+②得:5x=10m-5,得:x=2m-1.
①-②×2得:5y=5m+40,得:y=m+8.
又∵x,y的值都是正数,且x
解得
2m-1>0
m+8>0
2m-1
的解x,y的值都是正数,且x
x-2y=-17 ②
布置作业
请完成对应习题
