苏科版七年级下册导学案:7.5多边形的内角和与外角和(2) (word版无答案)
文档属性
| 名称 | 苏科版七年级下册导学案:7.5多边形的内角和与外角和(2) (word版无答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 321.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-18 00:00:00 | ||
图片预览

文档简介
《§7.5多边形的内角和与外角和(2)》学导单
班级_______ 姓名_________ 使用日期
【学习目标】:
1.通过不同方法探索多边形的内角和公式,并会利用它们进行有关计算.
2.历经探究多边形内角和公式的过程,体会说理的必要性.
3.运用结论进行有关推理与计算,培养学生的理性思维.
【学习重难点】:多边形的内角和公式 多边形的内角和公式的推导
【知识连接】: 多边形的概念:在平面内,由不在同一条直线上的3条或3条以上的线段首尾依次相接组成的图形叫做多边形。
对角线的概念:连接多边形不相邻的两个顶点的线段叫做多边形的对角线.
【导读指南】:
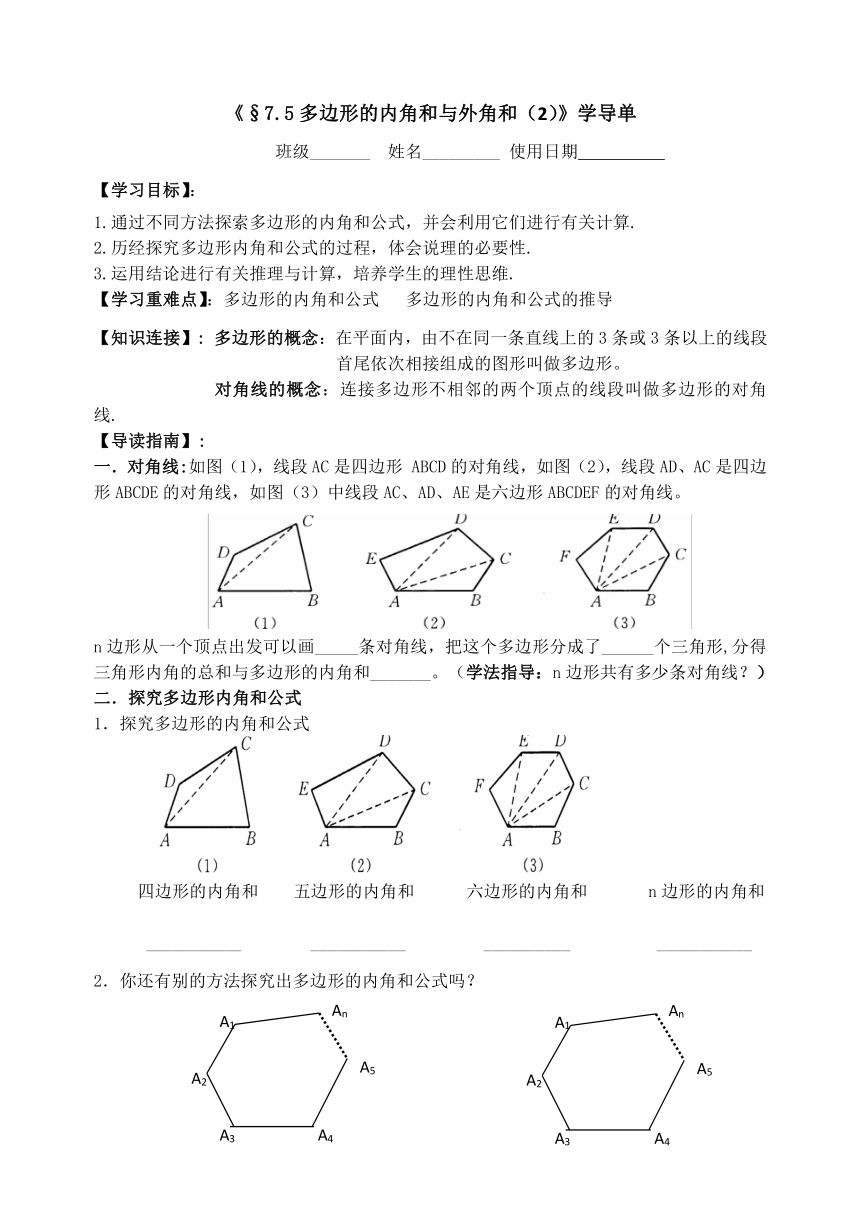
一.对角线:如图(1),线段AC是四边形 ABCD的对角线,如图(2),线段AD、AC是四边形ABCDE的对角线,如图(3)中线段AC、AD、AE是六边形ABCDEF的对角线。
n边形从一个顶点出发可以画_____条对角线,把这个多边形分成了______个三角形,分得三角形内角的总和与多边形的内角和_______。(学法指导:n边形共有多少条对角线?)
二.探究多边形内角和公式
1.探究多边形的内角和公式
2.你还有别的方法探究出多边形的内角和公式吗?
三.多边形内角和的应用
1.多边形内角和的相关计算
A例1.八边形的内角和等于 °.
练习1.求五边形的内角和。
2.某学生在计算四个多边形的内角和时,得到下列四个答案,其中错误的是( )
A.180° B. 540° C. 1900° D. 1080°
思考:内角和总是 的倍数.每增加一条边,内角和增加 °.
A例2.若多边形的内角和是1080°,则这个多边形是______边形.
练习:若多边形的内角和是1440°,则这个多边形是______边形.
A例3.若六边形的每个内角都相等,则每个内角都等于______°.
(学法指导:用方程的思想)
练习:如果一个n边形每一个内角都是135°,则n=______.
多边形内角和的综合应用
如图1,图2是边长均大于2的三角形、四边形.分别以它们的各顶点为圆心,以1为半径画弧与两邻边相交,得到3条弧、4条弧…、n条弧
(1)图1中3条弧的弧长的和为______,(2)图2中4条弧的弧长的和为______。
C拓展提升
1.一个多边形除去一个内角后,其余各内角的和为2750°,则这个内角是(? )
? A.110° B.120°?? C. 130°? D. 140°
2.已知:如图,在四边形ABCD中,∠A与∠C互补,BE平分 ∠ABC,DF平分∠ADC,
请问:∠1与∠2有什么样的数量关系?(学法指导:多边形的内角和公式)
《§7.5多边形的内角和与外角和(2)》当堂检测单
班级_________组别 姓名____________
A1.下列各角能成为一个多边形的内角和的只有 ( )
A 270? B 560? C 1980? D 1900?
A2.六边形的内角和等于 度.
A3. 如果一个多边形的内角和等于1800°,则这个多边形是______边形.
B4. 若n边形的每个内角都是150°,则n=____.
B5.在四边形ABCD中,∠A=90°,∠B∶∠C∶∠D=1∶2∶3,则∠B= ,∠C= ,∠D= .
(学法指导:四边形内角和为360?)
C6. 如图,五边形ABCDE的内角都相等,且∠1=∠2,∠3=∠4,求∠CAD的度数。
(学法指导:先求出五边形的每个内角)
班级_______ 姓名_________ 使用日期
【学习目标】:
1.通过不同方法探索多边形的内角和公式,并会利用它们进行有关计算.
2.历经探究多边形内角和公式的过程,体会说理的必要性.
3.运用结论进行有关推理与计算,培养学生的理性思维.
【学习重难点】:多边形的内角和公式 多边形的内角和公式的推导
【知识连接】: 多边形的概念:在平面内,由不在同一条直线上的3条或3条以上的线段首尾依次相接组成的图形叫做多边形。
对角线的概念:连接多边形不相邻的两个顶点的线段叫做多边形的对角线.
【导读指南】:
一.对角线:如图(1),线段AC是四边形 ABCD的对角线,如图(2),线段AD、AC是四边形ABCDE的对角线,如图(3)中线段AC、AD、AE是六边形ABCDEF的对角线。
n边形从一个顶点出发可以画_____条对角线,把这个多边形分成了______个三角形,分得三角形内角的总和与多边形的内角和_______。(学法指导:n边形共有多少条对角线?)
二.探究多边形内角和公式
1.探究多边形的内角和公式
2.你还有别的方法探究出多边形的内角和公式吗?
三.多边形内角和的应用
1.多边形内角和的相关计算
A例1.八边形的内角和等于 °.
练习1.求五边形的内角和。
2.某学生在计算四个多边形的内角和时,得到下列四个答案,其中错误的是( )
A.180° B. 540° C. 1900° D. 1080°
思考:内角和总是 的倍数.每增加一条边,内角和增加 °.
A例2.若多边形的内角和是1080°,则这个多边形是______边形.
练习:若多边形的内角和是1440°,则这个多边形是______边形.
A例3.若六边形的每个内角都相等,则每个内角都等于______°.
(学法指导:用方程的思想)
练习:如果一个n边形每一个内角都是135°,则n=______.
多边形内角和的综合应用
如图1,图2是边长均大于2的三角形、四边形.分别以它们的各顶点为圆心,以1为半径画弧与两邻边相交,得到3条弧、4条弧…、n条弧
(1)图1中3条弧的弧长的和为______,(2)图2中4条弧的弧长的和为______。
C拓展提升
1.一个多边形除去一个内角后,其余各内角的和为2750°,则这个内角是(? )
? A.110° B.120°?? C. 130°? D. 140°
2.已知:如图,在四边形ABCD中,∠A与∠C互补,BE平分 ∠ABC,DF平分∠ADC,
请问:∠1与∠2有什么样的数量关系?(学法指导:多边形的内角和公式)
《§7.5多边形的内角和与外角和(2)》当堂检测单
班级_________组别 姓名____________
A1.下列各角能成为一个多边形的内角和的只有 ( )
A 270? B 560? C 1980? D 1900?
A2.六边形的内角和等于 度.
A3. 如果一个多边形的内角和等于1800°,则这个多边形是______边形.
B4. 若n边形的每个内角都是150°,则n=____.
B5.在四边形ABCD中,∠A=90°,∠B∶∠C∶∠D=1∶2∶3,则∠B= ,∠C= ,∠D= .
(学法指导:四边形内角和为360?)
C6. 如图,五边形ABCDE的内角都相等,且∠1=∠2,∠3=∠4,求∠CAD的度数。
(学法指导:先求出五边形的每个内角)
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
