北师大版八年级数学下册课件 1.1 等腰三角形(1) (共27张PPT)
文档属性
| 名称 | 北师大版八年级数学下册课件 1.1 等腰三角形(1) (共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-18 10:03:39 | ||
图片预览







文档简介
初中数学八年级(下)
第1讲 等腰三角形(1)
三 角 形
证 明
公理
定义
真命题
定理
证明
证 明
《几何原本》(徐光启译)
证 明
1.两点确定一条直线.
2.两点之间线段最短.
3.同一平面内,过一点有且只有一条直线与已知直线垂直.
4.同位角相等,两直线平行.
5.过直线外一点有且只有一条直线与这条直线平行.
6.两边及其夹角分别相等的两个三角形全等.(SAS)
7.两角及其夹边分别相等的两个三角形全等.(ASA)
8.三边分别相等的两个三角形全等.(SSS)
作为证明依据的八条基本事实
证 明
定理 两角分别相等且其中一组等角的对边相等的两个三角形全等.(AAS)
证明小结
①画
②译
③析
④写
证明的一般步骤
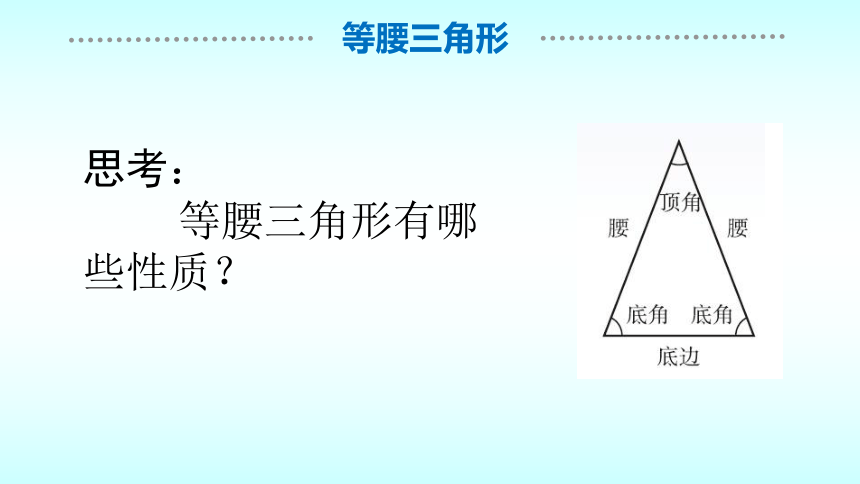
等腰三角形
思考:
等腰三角形有哪些性质?
等腰三角形
等腰三角形的性质
1.等腰三角形是轴对称图形,顶角平分线所在的直线是它的对称轴.
2.等腰三角形两底角相等(等边对等角).
3.等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重
合(三线合一).
4.等腰三角形两底角的平分线相等.
5.等腰三角形两腰上的高相等.
6.等腰三角形两腰上的中线相等.
7.等边三角形三条边相等,三个角都是60°.
......
等腰三角形
证明:等腰三角形两底角相等(等边对等角).
已知:在△ABC中,AB=AC.
求证:∠B=∠C.
等腰三角形
证明:等腰三角形两底角相等(等边对等角).
已知:在△ABC中,AB=AC.
求证:∠B=∠C.
D
证明:取BC的中点D,连接AD.
∵AB=AC,BD=CD,AD=AD,
∴△ABD≌△ACD(SSS).
∴∠B=∠C(全等三角形对应角相等).
等腰三角形
证明:等腰三角形两底角相等(等边对等角).
已知:在△ABC中,AB=AC.
求证:∠B=∠C.
D
证明:作∠BAC的角平分线交BC于D.
∴∠BAD=∠CAD,
∵AB=AC,∠BAD=∠CAD,AD=AD,
∴△ABD≌△ACD(SAS).
∴∠B=∠C(全等三角形对应角相等).
等腰三角形
证明:等腰三角形两底角相等(等边对等角).
已知:在△ABC中,AB=AC.
求证:∠B=∠C.
D
证明:作AD⊥BC于D,
则△ABD与△ACD均为直角三角形.
∴
∵AB=AC,AD=AD,
∴BD=CD
∴△ABD≌△ACD(SSS).
∴∠B=∠C(全等三角形对应角相等).
注:只有经过证明为真的命题才能作为证明依据.
—
—
等腰三角形
证明:等腰三角形两底角相等(等边对等角).
已知:在△ABC中,AB=AC.
求证:∠B=∠C.
证明:
在△ABC和△ACB中,
∵AB=AC,∠A=∠A,AC=AB,
∴△ABC≌△ACB(SAS)
∴∠B=∠C(全等三角形对应角相等).
证明小结
证明小结
4.证明的一般步骤:画—译—析—写.
2.我们经常通过三角形全等证明角相等.
3.证明的依据:公理、定义、真命题.
1.之前的操作验证往往能给我们提供证明思路.
等腰三角形
证明:等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合(三线合一).
D
AD是顶角平分线
AD是底边上的中线
AD是底边上的高线
AD是底边上的中线
AD是顶角平分线
AD是底边上的高线
AD是底边上的高线
AD是顶角平分线
AD是底边上的中线
等腰三角形
证明:等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合(三线合一).
D
已知:在△ABC中,AB=AC,AD平分∠BAC.
求证:BD=CD,AD⊥BC.
证明:
∵AB=AC,∠BAD=∠CAD,AD=AD,
∴△ABD≌△ACD(SAS),
∴BD=CD,∠BDA=∠CDA,
∵∠BDA+∠CDA=180°,
∴AD⊥BC
等腰三角形
证明:等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合(三线合一).
D
已知:在△ABC中,AB=AC,BD=CD.
求证:∠BAD=∠CAD,AD⊥BC.
证明:
∵AB=AC,BD=CD,AD=AD,
∴△ABD≌△ACD(SSS),
∴∠BAD=∠CAD,∠BDA=∠CDA,
∵∠BDA+∠CDA=180°,
∴AD⊥BC
等腰三角形
证明:等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合(三线合一).
D
已知:在△ABC中,AB=AC,AD⊥BC.
求证:∠BAD=∠CAD,BD=CD.
证明:
∵AB=AC,
∴∠B=∠C,
又∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∵∠ADB=∠ADC,∠B=∠C,
AB=AC,
∴△ABD≌△ACD(AAS),
∴BD=CD
学习小结
学习小结
公理
定义
真命题
定理
证明
学习小结
八条基本事实
1.两点确定一条直线.
2.两点之间线段最短.
3.同一平面内,过一点有且只有一条直线与已知直线
垂直.
4.同位角相等,两直线平行.
5.过直线外一点有且只有一条直线与这条直线平行.
6.两边及其夹角分别相等的两个三角形全等.(SAS)
7.两角及其夹边分别相等的两个三角形全等.(ASA)
8.三边分别相等的两个三角形全等.(SSS)
证明依据:公理、定义、真命题
三条本节课已证定理
1.两角分别相等且其中一组等角的对边相等的两个三角形全等.(AAS)
2.等腰三角形两底角相等.
3.等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合(三线合一).
学习小结
证明方法
①画
②译
③析
④写
课堂练习
课本P3 随堂练习
课堂练习
课本随堂练习答案
1.(1)∠C=70°;(2)∠A=36°
2.(1)证明:
∵AC⊥BD,
∴∠ACB=∠ACD=90°,
∵AC=AC,∠ACB=∠ACD,BC=CD,
∴△ABC≌△ADC(SAS),
∴AB=AD,
∴△ABD是等腰三角形.
(2)证明:
∵AC=BC,AC=CD
∴∠1=∠B,∠2=∠D
∴∠BAD=∠1+∠2=(∠1+∠2+∠B+∠D)÷2
=90°
第1讲 等腰三角形(1)
三 角 形
证 明
公理
定义
真命题
定理
证明
证 明
《几何原本》(徐光启译)
证 明
1.两点确定一条直线.
2.两点之间线段最短.
3.同一平面内,过一点有且只有一条直线与已知直线垂直.
4.同位角相等,两直线平行.
5.过直线外一点有且只有一条直线与这条直线平行.
6.两边及其夹角分别相等的两个三角形全等.(SAS)
7.两角及其夹边分别相等的两个三角形全等.(ASA)
8.三边分别相等的两个三角形全等.(SSS)
作为证明依据的八条基本事实
证 明
定理 两角分别相等且其中一组等角的对边相等的两个三角形全等.(AAS)
证明小结
①画
②译
③析
④写
证明的一般步骤
等腰三角形
思考:
等腰三角形有哪些性质?
等腰三角形
等腰三角形的性质
1.等腰三角形是轴对称图形,顶角平分线所在的直线是它的对称轴.
2.等腰三角形两底角相等(等边对等角).
3.等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重
合(三线合一).
4.等腰三角形两底角的平分线相等.
5.等腰三角形两腰上的高相等.
6.等腰三角形两腰上的中线相等.
7.等边三角形三条边相等,三个角都是60°.
......
等腰三角形
证明:等腰三角形两底角相等(等边对等角).
已知:在△ABC中,AB=AC.
求证:∠B=∠C.
等腰三角形
证明:等腰三角形两底角相等(等边对等角).
已知:在△ABC中,AB=AC.
求证:∠B=∠C.
D
证明:取BC的中点D,连接AD.
∵AB=AC,BD=CD,AD=AD,
∴△ABD≌△ACD(SSS).
∴∠B=∠C(全等三角形对应角相等).
等腰三角形
证明:等腰三角形两底角相等(等边对等角).
已知:在△ABC中,AB=AC.
求证:∠B=∠C.
D
证明:作∠BAC的角平分线交BC于D.
∴∠BAD=∠CAD,
∵AB=AC,∠BAD=∠CAD,AD=AD,
∴△ABD≌△ACD(SAS).
∴∠B=∠C(全等三角形对应角相等).
等腰三角形
证明:等腰三角形两底角相等(等边对等角).
已知:在△ABC中,AB=AC.
求证:∠B=∠C.
D
证明:作AD⊥BC于D,
则△ABD与△ACD均为直角三角形.
∴
∵AB=AC,AD=AD,
∴BD=CD
∴△ABD≌△ACD(SSS).
∴∠B=∠C(全等三角形对应角相等).
注:只有经过证明为真的命题才能作为证明依据.
—
—
等腰三角形
证明:等腰三角形两底角相等(等边对等角).
已知:在△ABC中,AB=AC.
求证:∠B=∠C.
证明:
在△ABC和△ACB中,
∵AB=AC,∠A=∠A,AC=AB,
∴△ABC≌△ACB(SAS)
∴∠B=∠C(全等三角形对应角相等).
证明小结
证明小结
4.证明的一般步骤:画—译—析—写.
2.我们经常通过三角形全等证明角相等.
3.证明的依据:公理、定义、真命题.
1.之前的操作验证往往能给我们提供证明思路.
等腰三角形
证明:等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合(三线合一).
D
AD是顶角平分线
AD是底边上的中线
AD是底边上的高线
AD是底边上的中线
AD是顶角平分线
AD是底边上的高线
AD是底边上的高线
AD是顶角平分线
AD是底边上的中线
等腰三角形
证明:等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合(三线合一).
D
已知:在△ABC中,AB=AC,AD平分∠BAC.
求证:BD=CD,AD⊥BC.
证明:
∵AB=AC,∠BAD=∠CAD,AD=AD,
∴△ABD≌△ACD(SAS),
∴BD=CD,∠BDA=∠CDA,
∵∠BDA+∠CDA=180°,
∴AD⊥BC
等腰三角形
证明:等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合(三线合一).
D
已知:在△ABC中,AB=AC,BD=CD.
求证:∠BAD=∠CAD,AD⊥BC.
证明:
∵AB=AC,BD=CD,AD=AD,
∴△ABD≌△ACD(SSS),
∴∠BAD=∠CAD,∠BDA=∠CDA,
∵∠BDA+∠CDA=180°,
∴AD⊥BC
等腰三角形
证明:等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合(三线合一).
D
已知:在△ABC中,AB=AC,AD⊥BC.
求证:∠BAD=∠CAD,BD=CD.
证明:
∵AB=AC,
∴∠B=∠C,
又∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∵∠ADB=∠ADC,∠B=∠C,
AB=AC,
∴△ABD≌△ACD(AAS),
∴BD=CD
学习小结
学习小结
公理
定义
真命题
定理
证明
学习小结
八条基本事实
1.两点确定一条直线.
2.两点之间线段最短.
3.同一平面内,过一点有且只有一条直线与已知直线
垂直.
4.同位角相等,两直线平行.
5.过直线外一点有且只有一条直线与这条直线平行.
6.两边及其夹角分别相等的两个三角形全等.(SAS)
7.两角及其夹边分别相等的两个三角形全等.(ASA)
8.三边分别相等的两个三角形全等.(SSS)
证明依据:公理、定义、真命题
三条本节课已证定理
1.两角分别相等且其中一组等角的对边相等的两个三角形全等.(AAS)
2.等腰三角形两底角相等.
3.等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合(三线合一).
学习小结
证明方法
①画
②译
③析
④写
课堂练习
课本P3 随堂练习
课堂练习
课本随堂练习答案
1.(1)∠C=70°;(2)∠A=36°
2.(1)证明:
∵AC⊥BD,
∴∠ACB=∠ACD=90°,
∵AC=AC,∠ACB=∠ACD,BC=CD,
∴△ABC≌△ADC(SAS),
∴AB=AD,
∴△ABD是等腰三角形.
(2)证明:
∵AC=BC,AC=CD
∴∠1=∠B,∠2=∠D
∴∠BAD=∠1+∠2=(∠1+∠2+∠B+∠D)÷2
=90°
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
