北师大版八年级下册2.5.2一元一次不等式与一次函数课件(共21张ppt)
文档属性
| 名称 | 北师大版八年级下册2.5.2一元一次不等式与一次函数课件(共21张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 603.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-18 09:45:28 | ||
图片预览








文档简介
北师大版 八年级下册
2.5 一元一次不等式与一次函数
一、温故知新
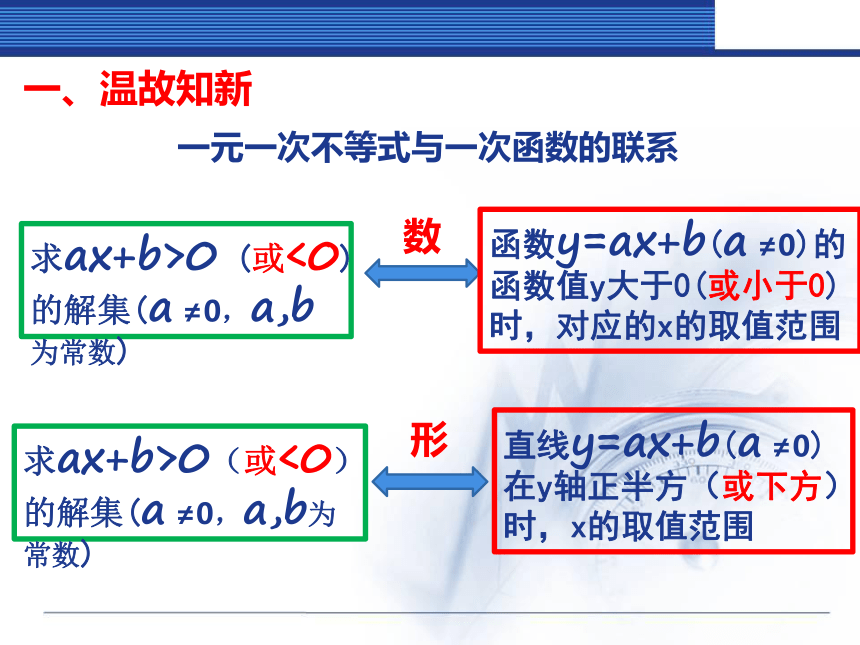
一元一次不等式与一次函数的联系
求ax+b>0 (或<0)的解集(a ≠0,a,b为常数)
求ax+b>0(或<0)的解集(a ≠0,a,b为常数)
函数y=ax+b(a ≠0)的函数值y大于0(或小于0)时,对应的x的取值范围
直线y=ax+b(a ≠0)在y轴正半方(或下方)时,x的取值范围
数
形
1.如图,一次函数y=kx+b的图象,不等式kx+b<0的解集为( )
A.x<-2.5 B.x>-2.5 C.x<-3 D.x>-3
-2.5
D
一、温故知新
y < 0
2.如图是一次函数y=kx-1的图象,当kx-1<2时,x的取值范围是( )
A. x<1 B. x>1
C. x<3 D. x>3
C
一、温故知新
y < 2
y = 2
3.已知,两个函数表达式为y1=-2x+6 ,y2=3x-4 ,
当y1 > y2 时,x的取值范围是( )
A. x>2 B. x<2
C. x=2 D.无法确定
B
一、温故知新
y1 > y2
-2x+6 > 3x-4
-5x > -10
x < 2
转化“不等式的问题”
4.如图,直线l1:y1=kx+b 与直线 l2:y2=x+a 在同一平面直角坐标系中的图象,则关于x不等式kx+b>x+a的解为( )
A. x>3 B. x<3
C. x=3 D.无法确定
B
一、温故知新
y1 > y2
l1:y1=kx+b
l2:y2=x+a
l1 高 l2低
高
低
转化“一次函数的问题”
x = 3
一、温故知新
一元一次不等式
ax+b>0 (ax+b<0)
(a ≠0,a,b为常数)
一次函数y=ax+b(a ≠0,a,b为常数)
函数y1=-2x+6 ,y2=3x-4 , x取何值时,y1 > y2 ?
转化“不等式的问题”
解不等式kx+b>x+a
转化“一次函数问题”
某电信公司有甲、乙两种手机收费业务.收费标准如下:
甲种业务:月租费10元,每通话1min收费0.3 元;
乙种业务:不收月租费,但每通话1min收费0.4元.
你认为顾客应该选择哪一种业务对顾客更合算?
二、探究新知
解:设顾客每月通话时长为 x min,
选择甲种业务每个月所需的费用为y1元,
选择乙种业务每个月所需的费用为y2元,得
y1=10+0.3x
y2=0.4x
变量:每个月通话时间,手机收费费用
一次函数
① 当y1= y2时,
②当y1>y2时,
③当y1甲:y1=10+0.3x 乙:y2=0.4x
得10+0.3x=0.4x,
得10+0.3x>0.4x,
得10+0.3x<0.4x,
解得x=100;
解得x<100;
解得x>100.
所以,当x=100时,甲乙两种业务消费额 一样
所以,当x<100时,选择乙种业务比较合算.
所以,当x>100时,选择甲种业务比较合算.
方案选择问题解题思路:
(1)根据题意,分别写出方案A、B的函数解析式yA,yB;
(2)将方案A、B进行三种情况分析:
①yA>yB ,
②yA ③yA=yB;
从而分别得到自变量的取值范围;
(3)根据实际情况选择方案.
例1:某单位计划组织员工去旅游,参加旅游人数估计为10~25人,
甲、乙两家旅行社的服务质量相同,且报价都是每人200元。经过协商,甲乙旅行社给予的优惠方案如下:
甲旅行社:给予每位游客七五折优惠;
乙旅行社:先免一位游客的旅游费用,其余游客八折优惠.
该单位选择哪一家旅行社支付的旅游费用较少?
三、巩固练习
解:设该单位参加这次旅游的人数是x人,
选择甲旅行社时,所需费用为y1元,
选择乙旅行社时,所需的费用为y2元,则
y1=200×0.75x
y2=200×0.8(x-1)
= 150x
=160x-160
变量:旅游人数,旅游费用
一次函数
解:设该单位参加这次旅游的人数是x人,选择甲旅行社时,所需费用为y1元,选择乙旅行社时,所需的费用为y2元,则
y1=200×0.75x =150x
y2=200×0.8(x-1)=160x-160
①当y1=y2时,
②当y1>y2时,
③当y1<y2时,
150x =160x-160,
150x >160x-160,
150x <160x-160,
解得x =16;
解得x<16;
解得x>16.
因为参加旅游的人数为10~25人,
所以,当x =16时,甲乙两家旅行社的收费相同;
当17≤x≤25时,选择甲旅行社费用较少,
当10≤x≤15时,选择乙旅行社费用较少.
总结归纳
一次函数刻画两个变量之间存在的一种相互依赖的关系
一元一次不等则描述两个变量满足某些特定条件时的状态
一元一次不等式
一次函数
1.公司40名员工到一景点集体参观,景点门票30元/人,该景点规定满40人可以购买团体体票,票价打八折.这天恰逢妇女节,该景点做活动,女士票价打5折,但不能同时享受两种优惠,请你帮助他们选择购票方案。
四、课堂检测
优惠
优惠条件
方案一
每名员工票价打八折
方案一
男员工票价30元,女员工的票价打五折
解:设该公司有x名女员工,则男员工有(40-x)名,选择团体票优惠时,所需费用为y1元,选择活动优惠时,所需的费用为y2元,则
y1=40×30×0.8 =960
y2=30×(40-x)+30×0.5x=1200-15x
①当y1=y2时,
②当y1>y2时,
③当y1<y2时,
960 = 1200-15x,
960>1200- 15x,
960< 1200-15x
解得x =16;
解得x >16;
解得x <16.
所以,当x =16时,选择团体票和活动相同;
当17≤x≤40时,选择活动优惠方式费用较少,
当0≤x≤15时,选择团体票优惠方式费用较少.
2.某单位要制作一批宣传材料.甲公司提出:
每份材料收费20元,另收3000元设计费;乙公司提出:每份材料收费30元,不收设计费.
(1)什么情况下选择甲公司比较合算?
(2)什么情况下选择乙公司比较合算?
(3)什么情况下两公司的收费相同?
3.某学校计划购买若干台电脑,现从两家商场了解到同一型号电脑每台报价均为6000元,并且多买都有一定的优惠.
甲商场的优惠条件是:第一台按原价收费,其余每台优惠25%;
乙商场的优惠条件是:每台优惠20%.
(1)什么情况下到甲商场购买更优惠?
(2)什么情况下到乙商场购买更优惠?
(3)什么情况下两家商场的收费相同?
解:设要买x台电脑,购买甲商场的电脑所需费用y1元,
购买乙商场的电脑所需费用为y2元.则有
y1=6000+(1-25%)(x-1)×6000=4500x+1500
y2=80%×6000x=4800x
①当y1<y2时,有4500x+1500<4800x,解得x>5
即当所购买电脑超过5台时,到甲商场购买更优惠;
②当y1>y2时,有4500x+1500>4800x,解得x<5.
即当所购买电脑少于5台时,到乙商场买更优惠;
③当y1=y2时,即4500x+1500=4800x,解得x=5.
即当所购买电脑为5台时,两家商场的收费相同.
五、课堂小结
解决实际问题步骤:
(1)理清题目中的数量关系,把这些数量关系分解为几个函数关系;
(2)列出这些函数关系式;
(3)根据题意,将列出的函数关系式转化为不等式;
(4)解不等式;
(5)选择符合题意的不等式的解集.
课本53页习题2.6
六、布置作业
千里之行,始于足下
2.5 一元一次不等式与一次函数
一、温故知新
一元一次不等式与一次函数的联系
求ax+b>0 (或<0)的解集(a ≠0,a,b为常数)
求ax+b>0(或<0)的解集(a ≠0,a,b为常数)
函数y=ax+b(a ≠0)的函数值y大于0(或小于0)时,对应的x的取值范围
直线y=ax+b(a ≠0)在y轴正半方(或下方)时,x的取值范围
数
形
1.如图,一次函数y=kx+b的图象,不等式kx+b<0的解集为( )
A.x<-2.5 B.x>-2.5 C.x<-3 D.x>-3
-2.5
D
一、温故知新
y < 0
2.如图是一次函数y=kx-1的图象,当kx-1<2时,x的取值范围是( )
A. x<1 B. x>1
C. x<3 D. x>3
C
一、温故知新
y < 2
y = 2
3.已知,两个函数表达式为y1=-2x+6 ,y2=3x-4 ,
当y1 > y2 时,x的取值范围是( )
A. x>2 B. x<2
C. x=2 D.无法确定
B
一、温故知新
y1 > y2
-2x+6 > 3x-4
-5x > -10
x < 2
转化“不等式的问题”
4.如图,直线l1:y1=kx+b 与直线 l2:y2=x+a 在同一平面直角坐标系中的图象,则关于x不等式kx+b>x+a的解为( )
A. x>3 B. x<3
C. x=3 D.无法确定
B
一、温故知新
y1 > y2
l1:y1=kx+b
l2:y2=x+a
l1 高 l2低
高
低
转化“一次函数的问题”
x = 3
一、温故知新
一元一次不等式
ax+b>0 (ax+b<0)
(a ≠0,a,b为常数)
一次函数y=ax+b(a ≠0,a,b为常数)
函数y1=-2x+6 ,y2=3x-4 , x取何值时,y1 > y2 ?
转化“不等式的问题”
解不等式kx+b>x+a
转化“一次函数问题”
某电信公司有甲、乙两种手机收费业务.收费标准如下:
甲种业务:月租费10元,每通话1min收费0.3 元;
乙种业务:不收月租费,但每通话1min收费0.4元.
你认为顾客应该选择哪一种业务对顾客更合算?
二、探究新知
解:设顾客每月通话时长为 x min,
选择甲种业务每个月所需的费用为y1元,
选择乙种业务每个月所需的费用为y2元,得
y1=10+0.3x
y2=0.4x
变量:每个月通话时间,手机收费费用
一次函数
① 当y1= y2时,
②当y1>y2时,
③当y1
得10+0.3x=0.4x,
得10+0.3x>0.4x,
得10+0.3x<0.4x,
解得x=100;
解得x<100;
解得x>100.
所以,当x=100时,甲乙两种业务消费额 一样
所以,当x<100时,选择乙种业务比较合算.
所以,当x>100时,选择甲种业务比较合算.
方案选择问题解题思路:
(1)根据题意,分别写出方案A、B的函数解析式yA,yB;
(2)将方案A、B进行三种情况分析:
①yA>yB ,
②yA
从而分别得到自变量的取值范围;
(3)根据实际情况选择方案.
例1:某单位计划组织员工去旅游,参加旅游人数估计为10~25人,
甲、乙两家旅行社的服务质量相同,且报价都是每人200元。经过协商,甲乙旅行社给予的优惠方案如下:
甲旅行社:给予每位游客七五折优惠;
乙旅行社:先免一位游客的旅游费用,其余游客八折优惠.
该单位选择哪一家旅行社支付的旅游费用较少?
三、巩固练习
解:设该单位参加这次旅游的人数是x人,
选择甲旅行社时,所需费用为y1元,
选择乙旅行社时,所需的费用为y2元,则
y1=200×0.75x
y2=200×0.8(x-1)
= 150x
=160x-160
变量:旅游人数,旅游费用
一次函数
解:设该单位参加这次旅游的人数是x人,选择甲旅行社时,所需费用为y1元,选择乙旅行社时,所需的费用为y2元,则
y1=200×0.75x =150x
y2=200×0.8(x-1)=160x-160
①当y1=y2时,
②当y1>y2时,
③当y1<y2时,
150x =160x-160,
150x >160x-160,
150x <160x-160,
解得x =16;
解得x<16;
解得x>16.
因为参加旅游的人数为10~25人,
所以,当x =16时,甲乙两家旅行社的收费相同;
当17≤x≤25时,选择甲旅行社费用较少,
当10≤x≤15时,选择乙旅行社费用较少.
总结归纳
一次函数刻画两个变量之间存在的一种相互依赖的关系
一元一次不等则描述两个变量满足某些特定条件时的状态
一元一次不等式
一次函数
1.公司40名员工到一景点集体参观,景点门票30元/人,该景点规定满40人可以购买团体体票,票价打八折.这天恰逢妇女节,该景点做活动,女士票价打5折,但不能同时享受两种优惠,请你帮助他们选择购票方案。
四、课堂检测
优惠
优惠条件
方案一
每名员工票价打八折
方案一
男员工票价30元,女员工的票价打五折
解:设该公司有x名女员工,则男员工有(40-x)名,选择团体票优惠时,所需费用为y1元,选择活动优惠时,所需的费用为y2元,则
y1=40×30×0.8 =960
y2=30×(40-x)+30×0.5x=1200-15x
①当y1=y2时,
②当y1>y2时,
③当y1<y2时,
960 = 1200-15x,
960>1200- 15x,
960< 1200-15x
解得x =16;
解得x >16;
解得x <16.
所以,当x =16时,选择团体票和活动相同;
当17≤x≤40时,选择活动优惠方式费用较少,
当0≤x≤15时,选择团体票优惠方式费用较少.
2.某单位要制作一批宣传材料.甲公司提出:
每份材料收费20元,另收3000元设计费;乙公司提出:每份材料收费30元,不收设计费.
(1)什么情况下选择甲公司比较合算?
(2)什么情况下选择乙公司比较合算?
(3)什么情况下两公司的收费相同?
3.某学校计划购买若干台电脑,现从两家商场了解到同一型号电脑每台报价均为6000元,并且多买都有一定的优惠.
甲商场的优惠条件是:第一台按原价收费,其余每台优惠25%;
乙商场的优惠条件是:每台优惠20%.
(1)什么情况下到甲商场购买更优惠?
(2)什么情况下到乙商场购买更优惠?
(3)什么情况下两家商场的收费相同?
解:设要买x台电脑,购买甲商场的电脑所需费用y1元,
购买乙商场的电脑所需费用为y2元.则有
y1=6000+(1-25%)(x-1)×6000=4500x+1500
y2=80%×6000x=4800x
①当y1<y2时,有4500x+1500<4800x,解得x>5
即当所购买电脑超过5台时,到甲商场购买更优惠;
②当y1>y2时,有4500x+1500>4800x,解得x<5.
即当所购买电脑少于5台时,到乙商场买更优惠;
③当y1=y2时,即4500x+1500=4800x,解得x=5.
即当所购买电脑为5台时,两家商场的收费相同.
五、课堂小结
解决实际问题步骤:
(1)理清题目中的数量关系,把这些数量关系分解为几个函数关系;
(2)列出这些函数关系式;
(3)根据题意,将列出的函数关系式转化为不等式;
(4)解不等式;
(5)选择符合题意的不等式的解集.
课本53页习题2.6
六、布置作业
千里之行,始于足下
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
