北师大版九年级下册3.4.3:圆内接四边形 课件(共20张PPT)
文档属性
| 名称 | 北师大版九年级下册3.4.3:圆内接四边形 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 411.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-18 00:00:00 | ||
图片预览






文档简介
3.4 圆周角和圆心角的关系
第3课时 圆内接四边形
一、圆内接四边形及其对角的性质
二、圆内接四边形外角的性质
学习目标
前边我学习了圆的内接三角形,圆的内接三角形有哪些性质呢?今天我们探究的圆的内接四边形的性质,我们根据圆内接三角形的定义,想一想如何给圆内接四边形下定义呢?
圆内接四边形及其对角的性质
圆内接多边形:在圆内相异n个点,按顺(或逆)时针
的方向连接相邻的各点,可形成一个n边形,此n边形叫
作此圆的圆内接多边形,此圆为多边形的外接圆.
圆心为此n边形的外心.
外心到圆内接多边形各顶点的距离皆等长(即外接圆的
半径)
下面,我们探究四边形与圆的关系.
四个顶点都在同一个圆上的四边形叫做圆内接四边形,这个圆叫做四边形的外接圆.
如图,四边形ABCD为⊙O的内接四边形,⊙O为四边形ABCD的外接圆.
四个顶点都在同一个圆上的四边形叫
做圆内接四边形,这个圆叫做四边形
的外接圆.
定义
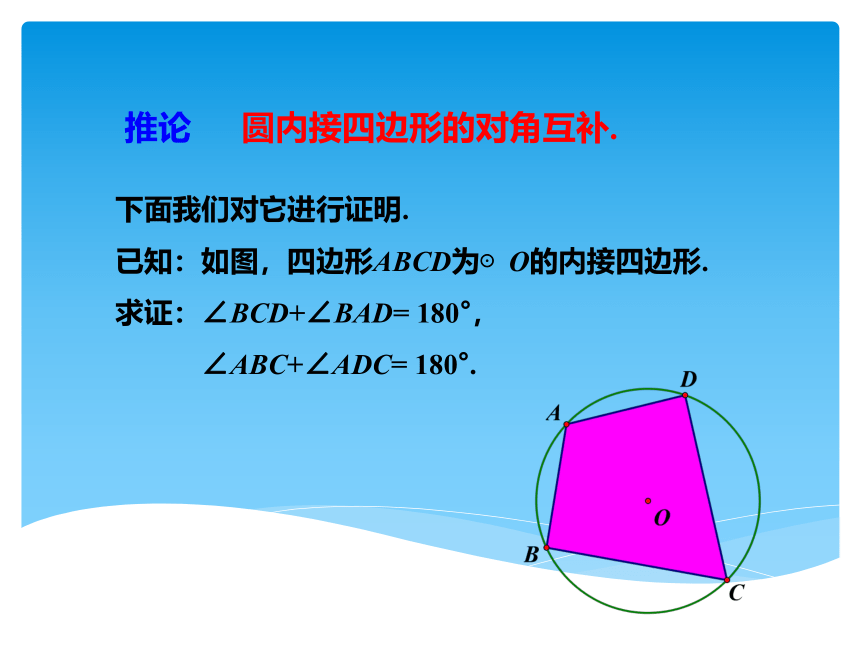
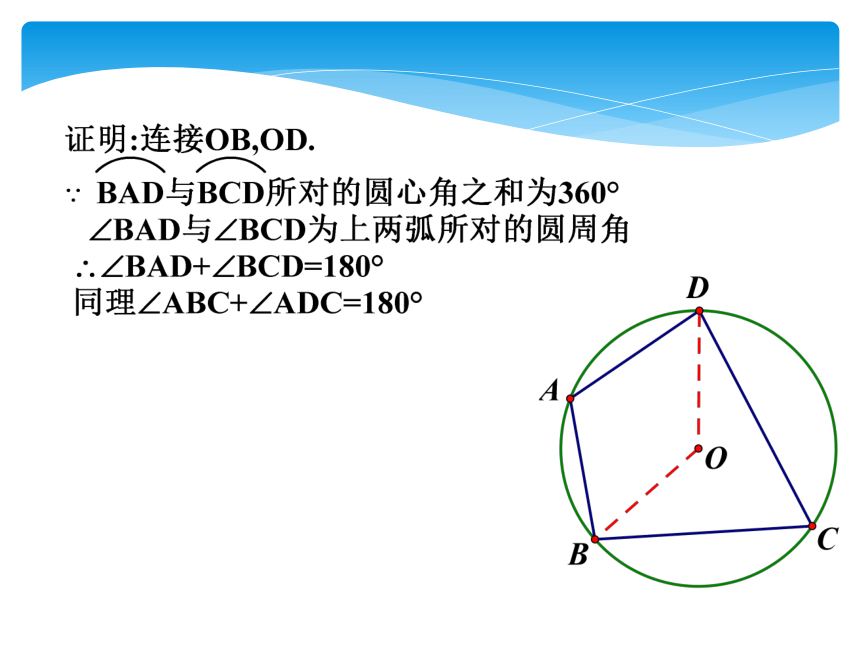
下面我们对它进行证明.
已知:如图,四边形ABCD为⊙O的内接四边形.
求证:∠BCD+∠BAD= 180°,
∠ABC+∠ADC= 180°.
推论 圆内接四边形的对角互补.
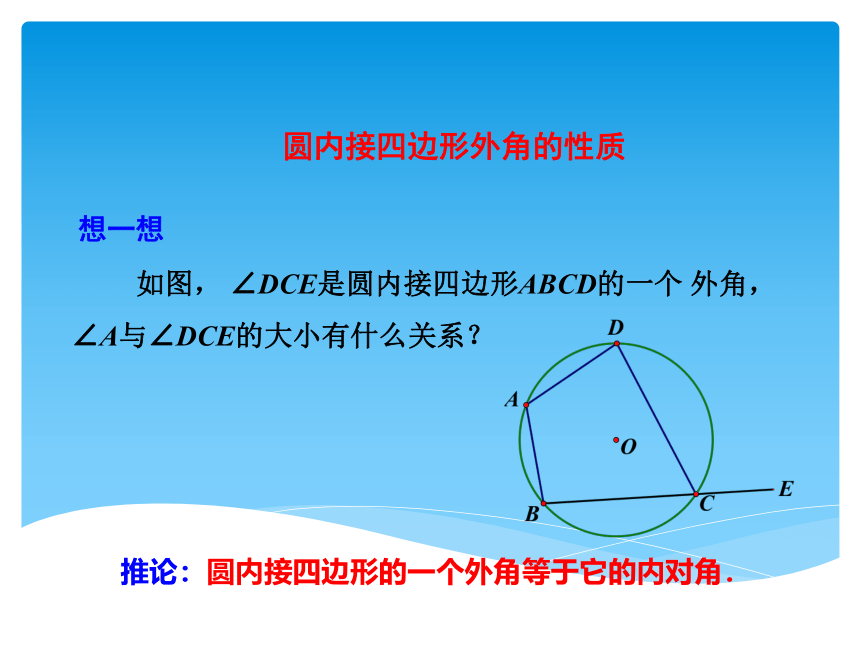
圆内接四边形外角的性质
想一想
如图, ∠DCE是圆内接四边形ABCD的一个 外角,
∠A与∠DCE的大小有什么关系?
推论:圆内接四边形的一个外角等于它的内对角.
1.下列说法正确的是( )
A.在圆内部的多边形叫做圆内接多边形
B.过四边形的四个顶点的圆叫做这个四边形的外接圆
C.任意一个四边形都有外接圆
D.一个圆只有唯一一个内接四边形
B
小试牛刀
D
B
B
A
D
7.【2019·天水】如图,四边形ABCD是菱形,⊙O经过点A,C,D,与BC相交于点E,连接AC,AE.若∠D=80°,则∠EAC的度数为( )
A.20° B.25° C.30° D.35°
C
C
圆内接四边形的角的“两种关系”:
(1)对角互补,若四边形ABCD为⊙O的内接四边形,
则∠A+∠C=180°,∠B+∠D=180°.
(2)任一外角与其相邻的内角的对角相等,简称圆内
接四边形的外角等于其内对角.
今天我们学了什么?
第3课时 圆内接四边形
一、圆内接四边形及其对角的性质
二、圆内接四边形外角的性质
学习目标
前边我学习了圆的内接三角形,圆的内接三角形有哪些性质呢?今天我们探究的圆的内接四边形的性质,我们根据圆内接三角形的定义,想一想如何给圆内接四边形下定义呢?
圆内接四边形及其对角的性质
圆内接多边形:在圆内相异n个点,按顺(或逆)时针
的方向连接相邻的各点,可形成一个n边形,此n边形叫
作此圆的圆内接多边形,此圆为多边形的外接圆.
圆心为此n边形的外心.
外心到圆内接多边形各顶点的距离皆等长(即外接圆的
半径)
下面,我们探究四边形与圆的关系.
四个顶点都在同一个圆上的四边形叫做圆内接四边形,这个圆叫做四边形的外接圆.
如图,四边形ABCD为⊙O的内接四边形,⊙O为四边形ABCD的外接圆.
四个顶点都在同一个圆上的四边形叫
做圆内接四边形,这个圆叫做四边形
的外接圆.
定义
下面我们对它进行证明.
已知:如图,四边形ABCD为⊙O的内接四边形.
求证:∠BCD+∠BAD= 180°,
∠ABC+∠ADC= 180°.
推论 圆内接四边形的对角互补.
圆内接四边形外角的性质
想一想
如图, ∠DCE是圆内接四边形ABCD的一个 外角,
∠A与∠DCE的大小有什么关系?
推论:圆内接四边形的一个外角等于它的内对角.
1.下列说法正确的是( )
A.在圆内部的多边形叫做圆内接多边形
B.过四边形的四个顶点的圆叫做这个四边形的外接圆
C.任意一个四边形都有外接圆
D.一个圆只有唯一一个内接四边形
B
小试牛刀
D
B
B
A
D
7.【2019·天水】如图,四边形ABCD是菱形,⊙O经过点A,C,D,与BC相交于点E,连接AC,AE.若∠D=80°,则∠EAC的度数为( )
A.20° B.25° C.30° D.35°
C
C
圆内接四边形的角的“两种关系”:
(1)对角互补,若四边形ABCD为⊙O的内接四边形,
则∠A+∠C=180°,∠B+∠D=180°.
(2)任一外角与其相邻的内角的对角相等,简称圆内
接四边形的外角等于其内对角.
今天我们学了什么?
