北师大版七年级数学下册《4.3_探索三角形全等的条件(1)》教学课件(共25张PPT)
文档属性
| 名称 | 北师大版七年级数学下册《4.3_探索三角形全等的条件(1)》教学课件(共25张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-18 10:47:22 | ||
图片预览






文档简介
这个风筝真好看,
我也想要一个和
它一模一样的!
1.掌握三角形全等的“边边边”条件,了解三角形
的稳定性.
2.经历探索三角形全等条件的过程,体会利用画
图、操作、归纳获得数学结论的过程,初步形成
解决问题的基本策略.
3. 在探索三角形全等条件及其应用过程中,能够
进行有条理的思考并进行简单的推理,体会分类
讨论的数学思想在数学中的应用.
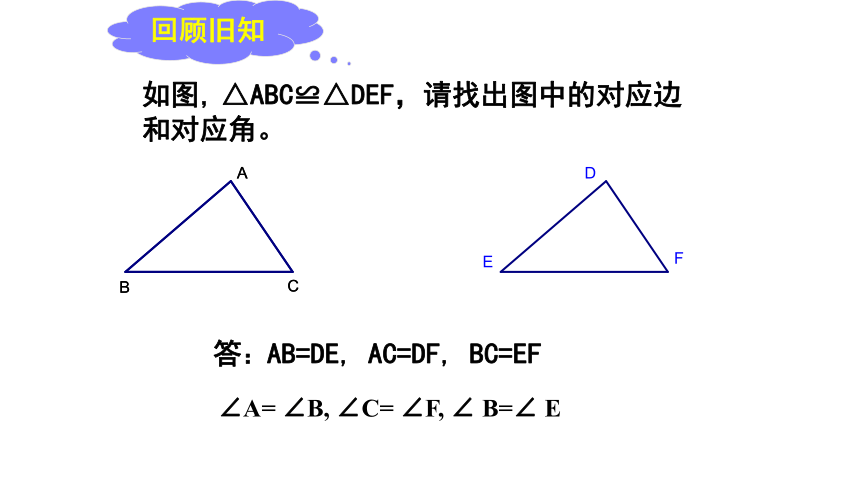
如图,△ABC≌△DEF,请找出图中的对应边和对应角。
答:AB=DE, AC=DF, BC=EF
∠A= ∠B, ∠C= ∠F, ∠ B=∠ E
回顾旧知
要画一个和已知三角形全等的三角形,需要几个与
边或角的大小有关的条件呢?
思考:
生活问题
(做风筝)
数学问题
(全等三角形)
转化
两个条件
(1) 三角形的一个角 ,一条边对应相等
(2)三角形的两条边对应相等
(3)三角形的两个角对应相等
一个条件
(1)有一条边对应相等的三角形
(2)有一个角对应相等的三角形
只给出两个条件时,不能保证所画的三角形一定全等.
只给出一个条件时,不能保证所画的三角形一定全等.
只给出一个或两个条件时,都不能保证所画的三角形一定全等.
议一议
若给出三个条件画三角形,你能说出有哪几种可能情况?
都给角:给三个角
2. 都给边:给三条边
3.既给角,又给边:
给两条边,一个角
给一条边,两个角
(1)
(2)
三个角对应相等的三角形不一定全等
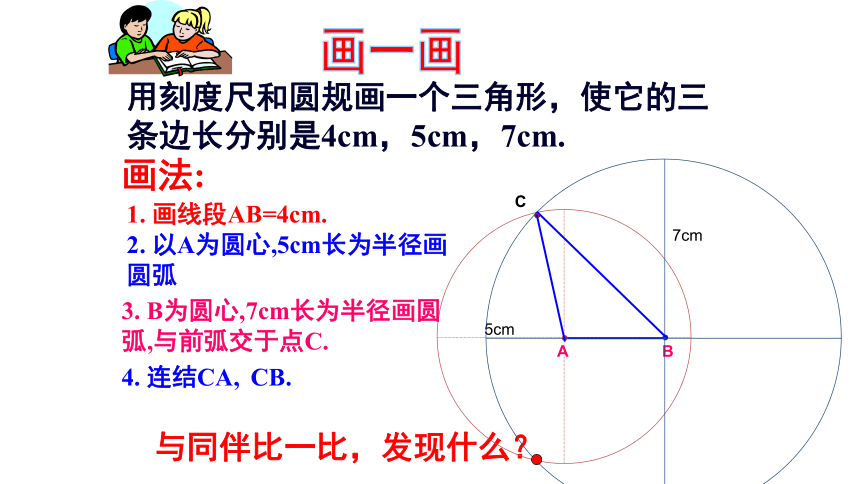
用刻度尺和圆规画一个三角形,使它的三条边长分别是4cm,5cm,7cm.
1. 画线段AB=4cm.
画法:
2. 以A为圆心,5cm长为半径画圆弧
4. 连结CA, CB.
与同伴比一比,发现什么?
A B
5cm
C
7cm
3. B为圆心,7cm长为半径画圆弧,与前弧交于点C.
有三条边对应相等的两个三角形全等
记做“边边边”或“SSS”
BC
BC
△DCB
A
B
C
D
巩固练习:
解: △ABC≌△DCB
理由如下:
AB = CD
∵ AC = BD
=
∴ △ABC ≌ ( )
SSS
如图,AB=CD,AC=BD,△ABC和△DCB是否全等?试说明理由.
公共边
例1 如图,当 AB=CD,BC=DA时,图中的△ABC与△CDA是否全等?并说明理由。
证明:
在△ABC与△CDA中
∴△ABC≌△CDA
(SSS)
∵
AB=CD
BC=DA
AC=CA
(已知)
(已知)
(公共边)
例题赏析
答:△ABC≌△CDA
∴∠3=∠4, ∠1=∠2 (全等三角形对应角相等)
答:AB∥CD. AD∥BC
∴AB∥CD, AD∥BC (内错角相等,两直线平行)
变式 如图,当 AB=CD,BC=DA时,你能说明AB与CD、AD与BC的位置关系吗?为什么?
证明:
在△ABC与△CDA中
∴△ABC≌△CDA
(SSS)
∵
AB=CD
AD=CB
AC=CA
(已知)
(已知)
(公共边)
1
2
3
4
1、已知: 如图,AC=AD ,BC=BD
求证:△ACB ≌ △ADB.
A
B
C
D
证明:
在△ACB与△ ADB中
∴△ACB ≌△ ADB
∵
AC=AD
BC=BD
AB=BA
(已知)
(已知)
(公共边)
(SSS)
2.已知:AC、BD相交于点O,且AB=DC,AC=DB,那么∠A=∠D吗?为什么?
答: ∠A=∠D
证明:
在△ABC和△DCB中
∵
∴△ABC≌△DCB (SSS)
∴∠A=∠D(全等三角形的对应角相等)
做一做
有一些长度适当的木条,用钉子把它们分别钉成三角形和四边形,并拉动它们.
三角形的大小和形状是固定不变的,而四边形的形状会改变.
只要三角形三边的长度确定了,这个三角形的形
状和大小就确定,三角形的这个性质叫
三角形的稳定性.
(1)只给出一个条件或两个条件时,都不能保证两个三角形全等.
(2)三个内角对应相等的两个三角形不一 定全等.
(3)边边边公理:三边对应相等的两个三角形全等,简写为“边边边”或“SSS”.
(4)三角形具有稳定性.
通过这节课的学习活动你有哪些收获?
你还有什么想法吗?
1. 如图,AB=AC, BD=CD, BH=CH. 图中有几组全等的三角形?它们全等的条件是什么?
解: 在△ABH和△ACH中
同理 △ABD≌△ACD
△DBH≌△DCH
( SSS)
∴△ABH≌△ACH
∵
六、达标检测
2.已知:如图,AB=DE, BC=EF, AF=CD.
(1) △ABC与△DEF是否全等?并说明理由。
(2) 求证:∠A=∠D
证明:
( SSS)
∴ ∠A=∠D
(全等三角形的对应角相等)
答:△ABC≌△DEF
∵AF = DC(已知)
∴AF+FC= DC+FC(等式的性质)
在△ABC和△DEF中
∵
AB = DE(已知)
BC = EF(已知)
AC = DF(已证)
∴△ABC≌△DEF
即AC=DF
已知:如图,A、D、B、E在同一直线上,AD=BE,AC=DF,BC=EF,那么△ABC≌△DEF吗? ∠E与∠ABC有什么关系?并证明你的结论。你能说明BC与EF的位置关系吗?并证明你的结论。
证明: ∵AD=BE(已知)
∴ AD+BD=BE+BD (等式的性质)
即AB=DE
在△ABC和△DEF 中
∵
∴ △ABC≌△DEF
(SSS)
∴ ∠ABC =∠E (全等三角形的对应角相等)
∴BC∥EF(同位角相等,两直线平行)
助学:P105 第10题
已知:如图AB=CD,AD=BC.
则∠A与∠C相等吗?为什么?
A
D
B
C
必做题:
选做题:
一个条件
(1)有一条边对应相等
的三角形
(2)有一个角对应相等
的三角形
一角为40o
一边长5cm
A
B
5cm
40o
只给出一个条件时,不能保证所画的三角形
一定全等.
两个条件
(1) 三角形的一个角
一条边对应相等
(2)三角形的两条边对应相等
(3)三角形的两个角对应相等
一内角30o ,一条边为3cm
两条边长分别为4cm、6cm
两个内角分别为40o、60o
A
B
30o
3cm
4cm
4cm
C1
C2
C
6cm
A
B
4cm
C
C1
C2
40o
60o
只给出两个条件时,不能保证所画的三角形
一定全等.
三个条件
三个角对应相等的三角形
三个角对应相等的三角形不一定全等
40o
60o
80o
40o
60o
议一议: 两个锐角对应相等的两个直角三角形全等吗?为什么?
我也想要一个和
它一模一样的!
1.掌握三角形全等的“边边边”条件,了解三角形
的稳定性.
2.经历探索三角形全等条件的过程,体会利用画
图、操作、归纳获得数学结论的过程,初步形成
解决问题的基本策略.
3. 在探索三角形全等条件及其应用过程中,能够
进行有条理的思考并进行简单的推理,体会分类
讨论的数学思想在数学中的应用.
如图,△ABC≌△DEF,请找出图中的对应边和对应角。
答:AB=DE, AC=DF, BC=EF
∠A= ∠B, ∠C= ∠F, ∠ B=∠ E
回顾旧知
要画一个和已知三角形全等的三角形,需要几个与
边或角的大小有关的条件呢?
思考:
生活问题
(做风筝)
数学问题
(全等三角形)
转化
两个条件
(1) 三角形的一个角 ,一条边对应相等
(2)三角形的两条边对应相等
(3)三角形的两个角对应相等
一个条件
(1)有一条边对应相等的三角形
(2)有一个角对应相等的三角形
只给出两个条件时,不能保证所画的三角形一定全等.
只给出一个条件时,不能保证所画的三角形一定全等.
只给出一个或两个条件时,都不能保证所画的三角形一定全等.
议一议
若给出三个条件画三角形,你能说出有哪几种可能情况?
都给角:给三个角
2. 都给边:给三条边
3.既给角,又给边:
给两条边,一个角
给一条边,两个角
(1)
(2)
三个角对应相等的三角形不一定全等
用刻度尺和圆规画一个三角形,使它的三条边长分别是4cm,5cm,7cm.
1. 画线段AB=4cm.
画法:
2. 以A为圆心,5cm长为半径画圆弧
4. 连结CA, CB.
与同伴比一比,发现什么?
A B
5cm
C
7cm
3. B为圆心,7cm长为半径画圆弧,与前弧交于点C.
有三条边对应相等的两个三角形全等
记做“边边边”或“SSS”
BC
BC
△DCB
A
B
C
D
巩固练习:
解: △ABC≌△DCB
理由如下:
AB = CD
∵ AC = BD
=
∴ △ABC ≌ ( )
SSS
如图,AB=CD,AC=BD,△ABC和△DCB是否全等?试说明理由.
公共边
例1 如图,当 AB=CD,BC=DA时,图中的△ABC与△CDA是否全等?并说明理由。
证明:
在△ABC与△CDA中
∴△ABC≌△CDA
(SSS)
∵
AB=CD
BC=DA
AC=CA
(已知)
(已知)
(公共边)
例题赏析
答:△ABC≌△CDA
∴∠3=∠4, ∠1=∠2 (全等三角形对应角相等)
答:AB∥CD. AD∥BC
∴AB∥CD, AD∥BC (内错角相等,两直线平行)
变式 如图,当 AB=CD,BC=DA时,你能说明AB与CD、AD与BC的位置关系吗?为什么?
证明:
在△ABC与△CDA中
∴△ABC≌△CDA
(SSS)
∵
AB=CD
AD=CB
AC=CA
(已知)
(已知)
(公共边)
1
2
3
4
1、已知: 如图,AC=AD ,BC=BD
求证:△ACB ≌ △ADB.
A
B
C
D
证明:
在△ACB与△ ADB中
∴△ACB ≌△ ADB
∵
AC=AD
BC=BD
AB=BA
(已知)
(已知)
(公共边)
(SSS)
2.已知:AC、BD相交于点O,且AB=DC,AC=DB,那么∠A=∠D吗?为什么?
答: ∠A=∠D
证明:
在△ABC和△DCB中
∵
∴△ABC≌△DCB (SSS)
∴∠A=∠D(全等三角形的对应角相等)
做一做
有一些长度适当的木条,用钉子把它们分别钉成三角形和四边形,并拉动它们.
三角形的大小和形状是固定不变的,而四边形的形状会改变.
只要三角形三边的长度确定了,这个三角形的形
状和大小就确定,三角形的这个性质叫
三角形的稳定性.
(1)只给出一个条件或两个条件时,都不能保证两个三角形全等.
(2)三个内角对应相等的两个三角形不一 定全等.
(3)边边边公理:三边对应相等的两个三角形全等,简写为“边边边”或“SSS”.
(4)三角形具有稳定性.
通过这节课的学习活动你有哪些收获?
你还有什么想法吗?
1. 如图,AB=AC, BD=CD, BH=CH. 图中有几组全等的三角形?它们全等的条件是什么?
解: 在△ABH和△ACH中
同理 △ABD≌△ACD
△DBH≌△DCH
( SSS)
∴△ABH≌△ACH
∵
六、达标检测
2.已知:如图,AB=DE, BC=EF, AF=CD.
(1) △ABC与△DEF是否全等?并说明理由。
(2) 求证:∠A=∠D
证明:
( SSS)
∴ ∠A=∠D
(全等三角形的对应角相等)
答:△ABC≌△DEF
∵AF = DC(已知)
∴AF+FC= DC+FC(等式的性质)
在△ABC和△DEF中
∵
AB = DE(已知)
BC = EF(已知)
AC = DF(已证)
∴△ABC≌△DEF
即AC=DF
已知:如图,A、D、B、E在同一直线上,AD=BE,AC=DF,BC=EF,那么△ABC≌△DEF吗? ∠E与∠ABC有什么关系?并证明你的结论。你能说明BC与EF的位置关系吗?并证明你的结论。
证明: ∵AD=BE(已知)
∴ AD+BD=BE+BD (等式的性质)
即AB=DE
在△ABC和△DEF 中
∵
∴ △ABC≌△DEF
(SSS)
∴ ∠ABC =∠E (全等三角形的对应角相等)
∴BC∥EF(同位角相等,两直线平行)
助学:P105 第10题
已知:如图AB=CD,AD=BC.
则∠A与∠C相等吗?为什么?
A
D
B
C
必做题:
选做题:
一个条件
(1)有一条边对应相等
的三角形
(2)有一个角对应相等
的三角形
一角为40o
一边长5cm
A
B
5cm
40o
只给出一个条件时,不能保证所画的三角形
一定全等.
两个条件
(1) 三角形的一个角
一条边对应相等
(2)三角形的两条边对应相等
(3)三角形的两个角对应相等
一内角30o ,一条边为3cm
两条边长分别为4cm、6cm
两个内角分别为40o、60o
A
B
30o
3cm
4cm
4cm
C1
C2
C
6cm
A
B
4cm
C
C1
C2
40o
60o
只给出两个条件时,不能保证所画的三角形
一定全等.
三个条件
三个角对应相等的三角形
三个角对应相等的三角形不一定全等
40o
60o
80o
40o
60o
议一议: 两个锐角对应相等的两个直角三角形全等吗?为什么?
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
