北师大版数学八年级下册1.1等腰三角形(1)课件(共31张)
文档属性
| 名称 | 北师大版数学八年级下册1.1等腰三角形(1)课件(共31张) |  | |
| 格式 | pptx | ||
| 文件大小 | 915.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-18 12:09:38 | ||
图片预览








文档简介
第一章 三角形的证明
1.1 等腰三角形(第1课时)
1
课堂讲解
全等三角形的性质和判定
等腰三角形的边、角性质
等腰三角形的“三线合一”
2
课时流程
逐点
导讲练
课堂小结
作业提升
学习目标
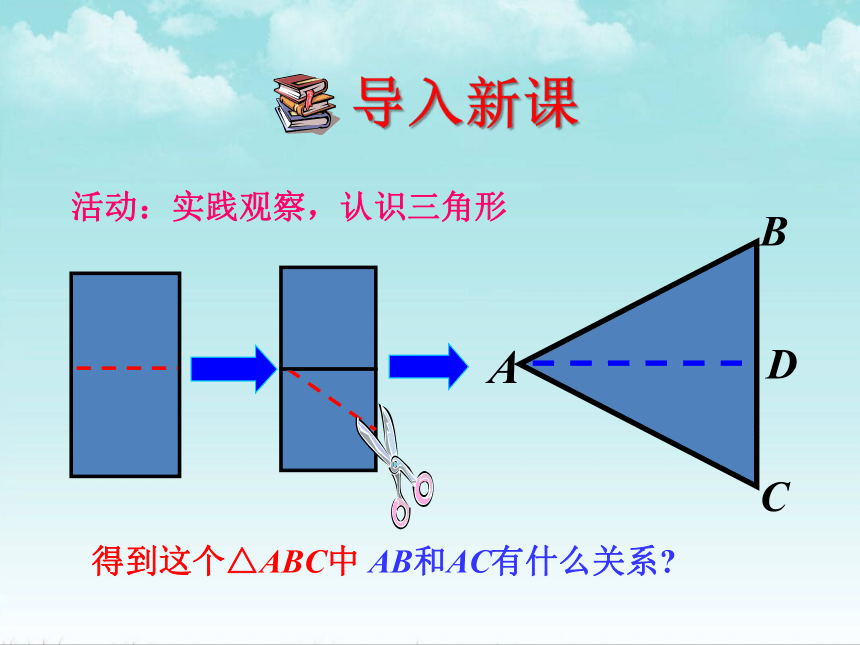
活动:实践观察,认识三角形
D
A
C
B
得到这个△ABC中 AB和AC有什么关系?
导入新课
1
知识点
全等三角形的性质和判定
全等三角形的定义是什么?
全等三角形有哪些性质?
全等三角形有哪些判定方法?
问题思考
1.全等三角形的性质:全等三角形的对应边相等、对应角相等.
2.全等三角形的判定方法
(1)三边分别相等的两个三角形全等(简写成“边边边”或“SSS”).
(2)两角及其夹边分别相等的两个三角形全等(简写成“角边角”或“ASA”).
(3)两角分别相等且其中一组等角的对边相等的两个三角形全等(简写成“角角边”或“AAS”).
(4)两边及其夹角分别相等的两个三角形全等(简写成“边角边”或“SAS”)
我们已经学过“两角及其中一角的对边对应相等相等的两个三角形全等(AAS)”这个结论,你能用有关的基本事实和已经学过的定理证明它吗?
想一想
证明:
∵ ∠A=∠A′,∠C=∠C′(已知)∴∠B=∠B′(三角形内角和定理)
在△ABC与△A′B′C′中
∵∠A=∠A′ (已知),
AB=A′B′(已知),
∠B=∠B′ (已证),
∴ △ABC≌△A′B′C′(ASA).
A
B
C
A′
B′
C′
●
●
● ●
● ●
已知:如图,在△ABC和△A′B′C′中, ∠A=∠A′, ∠C=∠C′, AB=A′B′.
求证:△ABC≌△A′B′C′.
利用全等三角形的判定方法,当∠D=∠B时,
两个三角形符合“边角边”,△ADF≌△CBE.
导引:
如图,点E,F在AC上,AD=BC,DF=BE,要使△ADF≌△CBE,还需要添加的一个条件是( )
A.∠A=∠C B.∠D=∠B
C.AD∥BC D.DF∥BE
B
练习
1
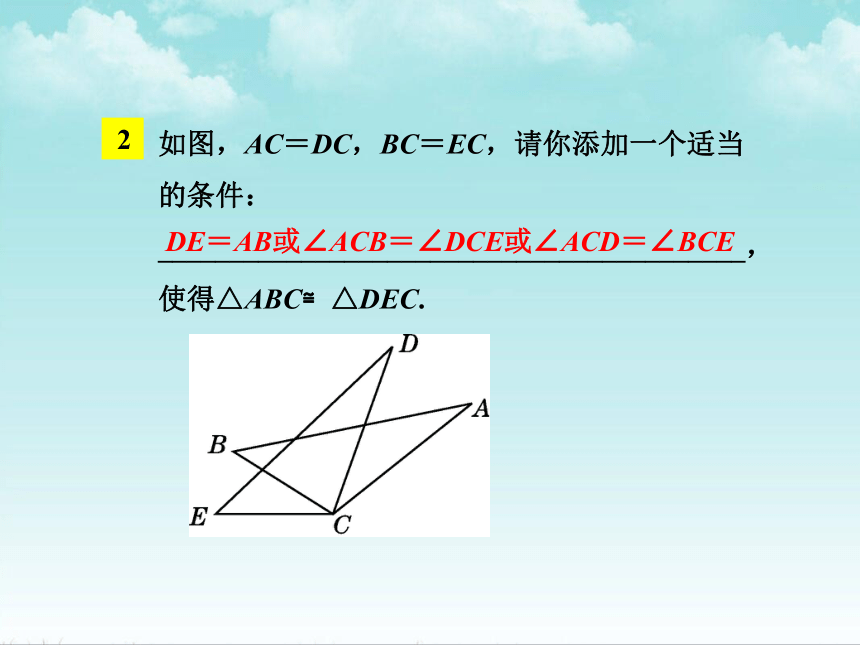
如图,AC=DC,BC=EC,请你添加一个适当的条件:_________________________________________,使得△ABC≌△DEC.
2
DE=AB或∠ACB=∠DCE或∠ACD=∠BCE
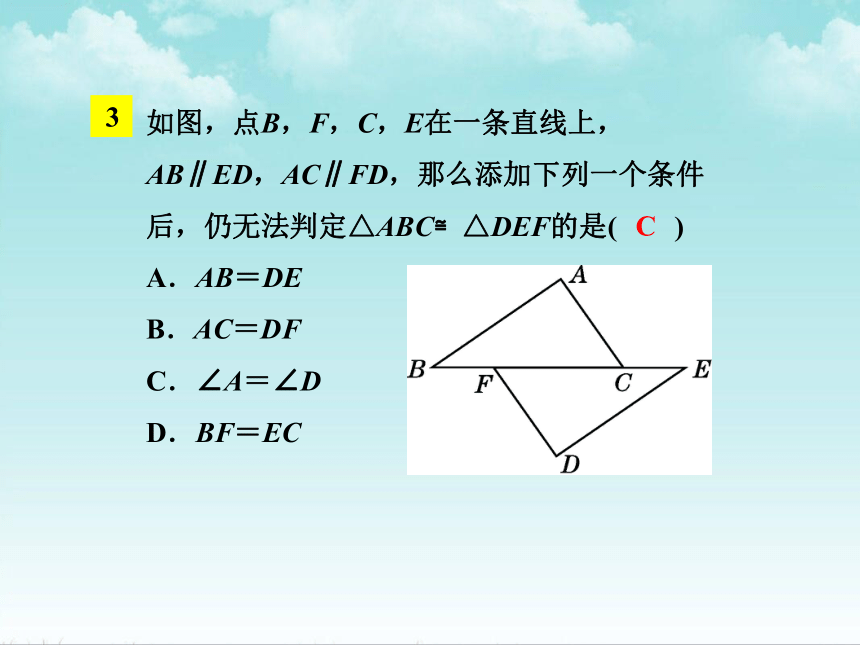
如图,点B,F,C,E在一条直线上,AB∥ED,AC∥FD,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是( )
A.AB=DE
B.AC=DF
C.∠A=∠D
D.BF=EC
3
C
2
知识点
等腰三角形的边、角性质
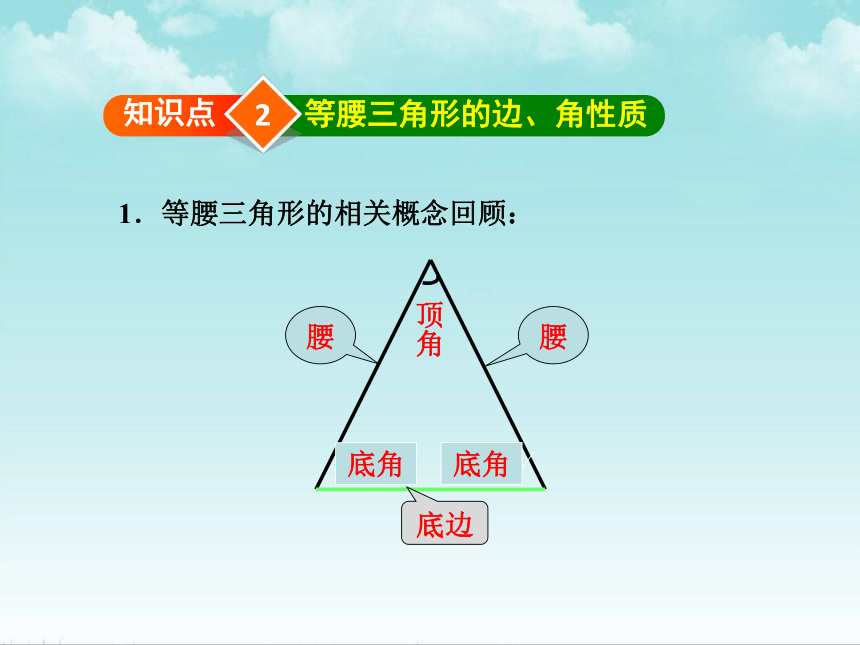
1.等腰三角形的相关概念回顾:
腰
腰
顶角
底角
底角
底边
(1)还记得我们探索过的等腰三角形的性质吗?
(2)请你选择等腰三角形的一条性质进行证明,并与同伴交流.
议一议
归纳
定理 等腰三角形的两底角相等.
这一定理可以简述为:等边对等角.
已知:如图1-1,在△ABC中,AB=AC.求证:∠B=∠C.
分析:我们曾经利用折叠的方法说明
了这两个底角相等(如图1-2).实际
上,折痕将等腰三角形分成了两
个全等三角形.这启发我们,可以
作一条辅助线,把原三角形分成
两个全等的三角形,从而证明这
两个底角相等.
图1-2
证明:如图1-3,取BC的中点D,连接 AD.
∵AB=AC,BD=CD,AD=AD,
∴△ABD≌△ACD ( SSS ).
∴ ∠B=∠C (全等三角形的对应角相等).
练习 (1)在△ABC中,AB=AC,若∠A=50°,求∠B;
(2)若等腰三角形的一个角为70°,求顶角的度数;
(3)若等腰三角形的一个角为90°,求顶角的度数.
导引:给出的条件中,若底角、顶角已确定,可直接运用三
角形的内角和定理与等腰三角形的两底角相等的性质
求解;若给出的条件中底角、顶角不确定,则要分两
种情况求解.
解:(1)∵AB=AC,∴∠B=∠C.
∵∠A+∠B+∠C=180°,
∴50°+2∠B=180°,解得∠B=65°.
练习
(2)由题意可知,70°的角可以为顶角或底角,当底角
为70°时,顶角为180°-70°×2=40°.因此顶角
为40°或70°.
(3)若顶角为90°,底角为 若底角为
90°,则三个内角的和大于180°,不符合三角形
内角和定理.因此顶角为90°.
总结
1.在等腰三角形中求角时,要看给出的角是否确定为顶角或底角.若已确定,则直接利用三角形的内角和定理求解;若没有指出所给的角是顶角还是底角,要分两种情况讨论,并看是否符合三角形内角和定理.
2.若等腰三角形中给出的一内角是直角或钝角,则此角必为顶角.
练习
如图,在△ABD中,AC⊥BD ,垂足为C,AC=BC=CD.
(1)求证:△ABD是等腰三角形;
(1)在△ACB和△ACD中,
所以△ACB≌△ACD(SAS).
所以AB=AD(全等三角形的对应边相等).
所以△ABD是等腰三角形.
证明:
A
(2)求∠BAD的度数.
因为AC=BC,
所以∠B=∠BAC.
因为∠ACB=90°,
所以∠BAC=45°.
同理∠DAC=45°,
所以∠BAD=∠BAC+∠DAC
=45°+45°=90°.
解:
A
3
知识点
等腰三角形的“三线合一”
想一想
在图1 -3中,线段AD还具有怎样的性质?为什么?由
此你能得到什么结论?
推论 等腰三角形的顶角平分线、底边上的中线、 底边上的高互相重合(简写成“三线合一”)
归纳
如图,在△ABC中,AB=AC,AD是BC边上的中线,∠ABC的平分线BG交AC于点G,交AD于点E,EF⊥AB,垂足为F.
(1)若∠BAD=25°,求∠C的度数;
(2)求证:EF=ED.
∵AB=AC,AD是BC边上的中线,
∴∠BAD=∠CAD.∴∠BAC=2∠BAD=50°.
∵AB=AC,
∴ ∠C=∠ABC = (180°-∠BAC)
= (180°-50°)=65°.
例1
(1)解:
(2)求证:EF=ED.
证明:∵AB=AC,AD是BC边上的中线,
∴ED⊥BC.
又∵BG平分∠ABC,EF⊥AB,
∴EF=ED.
1
如图,在△ABC中,AB=AC,D为BC的中点,∠BAD=35°,则∠C的度数为( )
A.35°
B.45°
C.55°
D.60°
C
随堂练习
2
如图,在△ABC中,AB=AC,点D是BC边的中点,点E在AD上,那么下列结论不一定正确的是( )
A.AD⊥BC
B.∠EBC=∠ECB
C.∠ABE=∠ACE
D.AE=BE
D
3
如图,在△ABC中,AB=AC,AD是角平分线,BE=CF,则下列说法正确的有( )
①DA平分∠EDF;②△EBD≌△FCD;
③BD=CD;④AD⊥BC.
A.1个
B.2个
C.3个
D.4个
D
1.知识方面:
(1)等腰三角形的性质:等边对等角.
(2)等腰三角形性质的推论:三线合一,即等腰三角
形顶角的平分线、底边上的中线及底边上的高线
互相重合.
2.思想方法:转化思想的应用,等腰三角形的性质是
证明角相等、边相等的重要方法.
1
知识小结
课堂小结
已知等腰三角形的一个外角等于110°,这个等腰三
角形的一个底角的度数为( )
A.40° B.55°
C.70° D.55°或70°
易错点:求等腰三角形的角时易出现漏解的错误
2
易错小结
D
本题应用分类讨论思想,分顶角为70°和底角为70°两种情况,解题时易丢掉一种情况而漏解.
课后作业
课后习题
1.1 等腰三角形(第1课时)
1
课堂讲解
全等三角形的性质和判定
等腰三角形的边、角性质
等腰三角形的“三线合一”
2
课时流程
逐点
导讲练
课堂小结
作业提升
学习目标
活动:实践观察,认识三角形
D
A
C
B
得到这个△ABC中 AB和AC有什么关系?
导入新课
1
知识点
全等三角形的性质和判定
全等三角形的定义是什么?
全等三角形有哪些性质?
全等三角形有哪些判定方法?
问题思考
1.全等三角形的性质:全等三角形的对应边相等、对应角相等.
2.全等三角形的判定方法
(1)三边分别相等的两个三角形全等(简写成“边边边”或“SSS”).
(2)两角及其夹边分别相等的两个三角形全等(简写成“角边角”或“ASA”).
(3)两角分别相等且其中一组等角的对边相等的两个三角形全等(简写成“角角边”或“AAS”).
(4)两边及其夹角分别相等的两个三角形全等(简写成“边角边”或“SAS”)
我们已经学过“两角及其中一角的对边对应相等相等的两个三角形全等(AAS)”这个结论,你能用有关的基本事实和已经学过的定理证明它吗?
想一想
证明:
∵ ∠A=∠A′,∠C=∠C′(已知)∴∠B=∠B′(三角形内角和定理)
在△ABC与△A′B′C′中
∵∠A=∠A′ (已知),
AB=A′B′(已知),
∠B=∠B′ (已证),
∴ △ABC≌△A′B′C′(ASA).
A
B
C
A′
B′
C′
●
●
● ●
● ●
已知:如图,在△ABC和△A′B′C′中, ∠A=∠A′, ∠C=∠C′, AB=A′B′.
求证:△ABC≌△A′B′C′.
利用全等三角形的判定方法,当∠D=∠B时,
两个三角形符合“边角边”,△ADF≌△CBE.
导引:
如图,点E,F在AC上,AD=BC,DF=BE,要使△ADF≌△CBE,还需要添加的一个条件是( )
A.∠A=∠C B.∠D=∠B
C.AD∥BC D.DF∥BE
B
练习
1
如图,AC=DC,BC=EC,请你添加一个适当的条件:_________________________________________,使得△ABC≌△DEC.
2
DE=AB或∠ACB=∠DCE或∠ACD=∠BCE
如图,点B,F,C,E在一条直线上,AB∥ED,AC∥FD,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是( )
A.AB=DE
B.AC=DF
C.∠A=∠D
D.BF=EC
3
C
2
知识点
等腰三角形的边、角性质
1.等腰三角形的相关概念回顾:
腰
腰
顶角
底角
底角
底边
(1)还记得我们探索过的等腰三角形的性质吗?
(2)请你选择等腰三角形的一条性质进行证明,并与同伴交流.
议一议
归纳
定理 等腰三角形的两底角相等.
这一定理可以简述为:等边对等角.
已知:如图1-1,在△ABC中,AB=AC.求证:∠B=∠C.
分析:我们曾经利用折叠的方法说明
了这两个底角相等(如图1-2).实际
上,折痕将等腰三角形分成了两
个全等三角形.这启发我们,可以
作一条辅助线,把原三角形分成
两个全等的三角形,从而证明这
两个底角相等.
图1-2
证明:如图1-3,取BC的中点D,连接 AD.
∵AB=AC,BD=CD,AD=AD,
∴△ABD≌△ACD ( SSS ).
∴ ∠B=∠C (全等三角形的对应角相等).
练习 (1)在△ABC中,AB=AC,若∠A=50°,求∠B;
(2)若等腰三角形的一个角为70°,求顶角的度数;
(3)若等腰三角形的一个角为90°,求顶角的度数.
导引:给出的条件中,若底角、顶角已确定,可直接运用三
角形的内角和定理与等腰三角形的两底角相等的性质
求解;若给出的条件中底角、顶角不确定,则要分两
种情况求解.
解:(1)∵AB=AC,∴∠B=∠C.
∵∠A+∠B+∠C=180°,
∴50°+2∠B=180°,解得∠B=65°.
练习
(2)由题意可知,70°的角可以为顶角或底角,当底角
为70°时,顶角为180°-70°×2=40°.因此顶角
为40°或70°.
(3)若顶角为90°,底角为 若底角为
90°,则三个内角的和大于180°,不符合三角形
内角和定理.因此顶角为90°.
总结
1.在等腰三角形中求角时,要看给出的角是否确定为顶角或底角.若已确定,则直接利用三角形的内角和定理求解;若没有指出所给的角是顶角还是底角,要分两种情况讨论,并看是否符合三角形内角和定理.
2.若等腰三角形中给出的一内角是直角或钝角,则此角必为顶角.
练习
如图,在△ABD中,AC⊥BD ,垂足为C,AC=BC=CD.
(1)求证:△ABD是等腰三角形;
(1)在△ACB和△ACD中,
所以△ACB≌△ACD(SAS).
所以AB=AD(全等三角形的对应边相等).
所以△ABD是等腰三角形.
证明:
A
(2)求∠BAD的度数.
因为AC=BC,
所以∠B=∠BAC.
因为∠ACB=90°,
所以∠BAC=45°.
同理∠DAC=45°,
所以∠BAD=∠BAC+∠DAC
=45°+45°=90°.
解:
A
3
知识点
等腰三角形的“三线合一”
想一想
在图1 -3中,线段AD还具有怎样的性质?为什么?由
此你能得到什么结论?
推论 等腰三角形的顶角平分线、底边上的中线、 底边上的高互相重合(简写成“三线合一”)
归纳
如图,在△ABC中,AB=AC,AD是BC边上的中线,∠ABC的平分线BG交AC于点G,交AD于点E,EF⊥AB,垂足为F.
(1)若∠BAD=25°,求∠C的度数;
(2)求证:EF=ED.
∵AB=AC,AD是BC边上的中线,
∴∠BAD=∠CAD.∴∠BAC=2∠BAD=50°.
∵AB=AC,
∴ ∠C=∠ABC = (180°-∠BAC)
= (180°-50°)=65°.
例1
(1)解:
(2)求证:EF=ED.
证明:∵AB=AC,AD是BC边上的中线,
∴ED⊥BC.
又∵BG平分∠ABC,EF⊥AB,
∴EF=ED.
1
如图,在△ABC中,AB=AC,D为BC的中点,∠BAD=35°,则∠C的度数为( )
A.35°
B.45°
C.55°
D.60°
C
随堂练习
2
如图,在△ABC中,AB=AC,点D是BC边的中点,点E在AD上,那么下列结论不一定正确的是( )
A.AD⊥BC
B.∠EBC=∠ECB
C.∠ABE=∠ACE
D.AE=BE
D
3
如图,在△ABC中,AB=AC,AD是角平分线,BE=CF,则下列说法正确的有( )
①DA平分∠EDF;②△EBD≌△FCD;
③BD=CD;④AD⊥BC.
A.1个
B.2个
C.3个
D.4个
D
1.知识方面:
(1)等腰三角形的性质:等边对等角.
(2)等腰三角形性质的推论:三线合一,即等腰三角
形顶角的平分线、底边上的中线及底边上的高线
互相重合.
2.思想方法:转化思想的应用,等腰三角形的性质是
证明角相等、边相等的重要方法.
1
知识小结
课堂小结
已知等腰三角形的一个外角等于110°,这个等腰三
角形的一个底角的度数为( )
A.40° B.55°
C.70° D.55°或70°
易错点:求等腰三角形的角时易出现漏解的错误
2
易错小结
D
本题应用分类讨论思想,分顶角为70°和底角为70°两种情况,解题时易丢掉一种情况而漏解.
课后作业
课后习题
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
