北师大版数学八年级下册课件:6.2平行四边形的判定(3)(共24张PPT)
文档属性
| 名称 | 北师大版数学八年级下册课件:6.2平行四边形的判定(3)(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-18 14:32:09 | ||
图片预览





文档简介
6.2平行四边形的判定(3)
1.平行四边形的定义是什么?它有什么作用?
2.平行四边形有哪些判断方法?
导入新课
1
知识点
平行线间的平行线段
在笔直的铁轨上,夹
在两根铁轨之间的平行枕
木是否一样长?你能说明
理由吗?与同伴交流.
感悟新知
例3
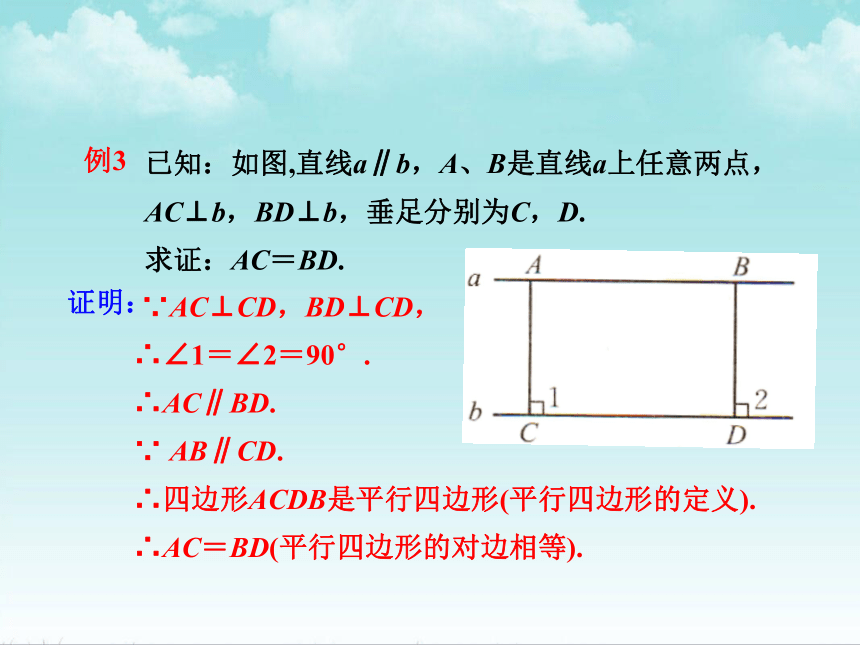
已知:如图,直线a∥b,A、B是直线a上任意两点,AC⊥b,BD⊥b,垂足分别为C,D.
求证:AC=BD.
∵AC⊥CD,BD⊥CD,
∴∠1=∠2=90°.
∴AC∥BD.
∵ AB∥CD.
∴四边形ACDB是平行四边形(平行四边形的定义).
∴AC=BD(平行四边形的对边相等).
证明:
数学表达式:
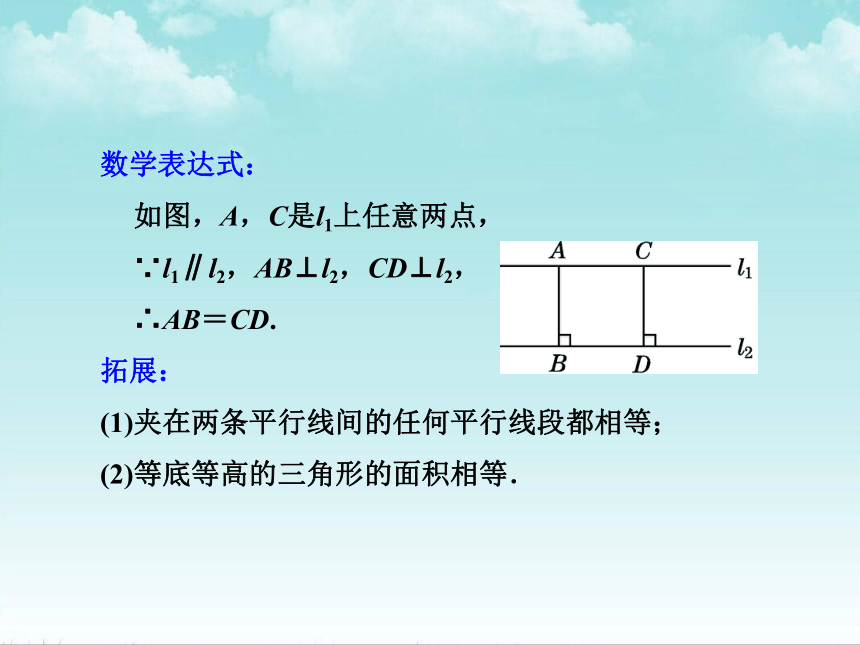
如图,A,C是l1上任意两点,
∵l1∥l2,AB⊥l2,CD⊥l2,
∴AB=CD.
拓展:
(1)夹在两条平行线间的任何平行线段都相等;
(2)等底等高的三角形的面积相等.
1
如图,在?ABCD中,E,F分别为BC,AD边上
的点,要使BF=DE,
需添加一个条件:_______________________.
BF∥DE(答案不唯一)
随堂练习
2
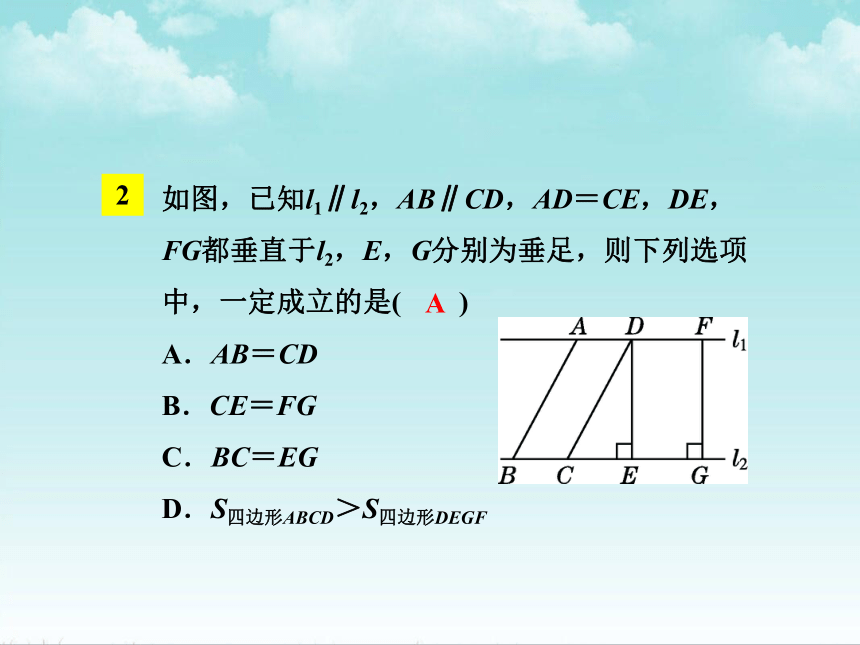
如图,已知l1∥l2,AB∥CD,AD=CE,DE,FG都垂直于l2,E,G分别为垂足,则下列选项中,一定成立的是( )
A.AB=CD
B.CE=FG
C.BC=EG
D.S四边形ABCD>S四边形DEGF
A
3
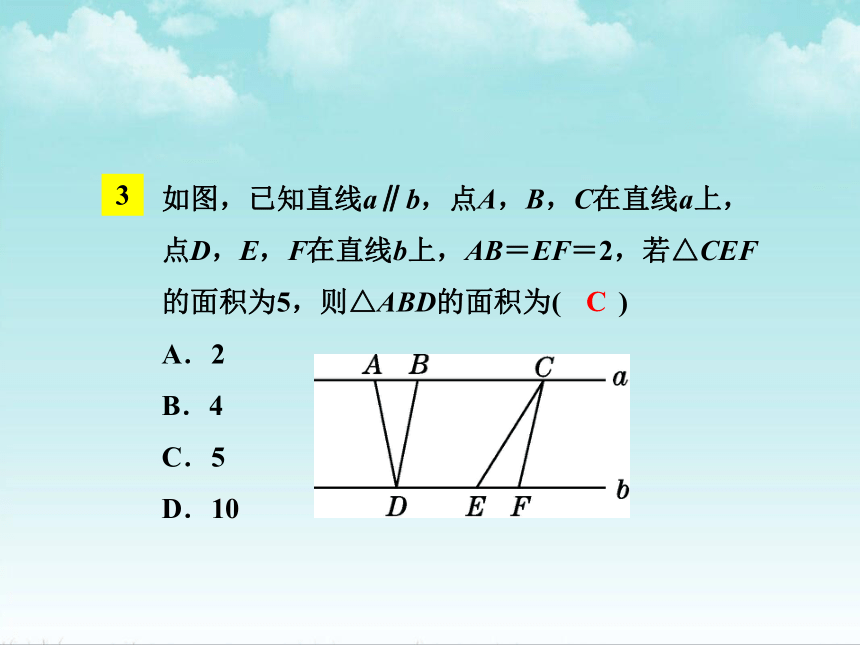
如图,已知直线a∥b,点A,B,C在直线a上,点D,E,F在直线b上,AB=EF=2,若△CEF的面积为5,则△ABD的面积为( )
A.2
B.4
C.5
D.10
C
4
如图,设点P是?ABCD的边AB上任意一点,设△APD的面积为S1,△BPC的面积为S2,△CDP的面积为S3,则( )
A.S3=S1+S2
B.S3>S1+S2
C.S3<S1+S2
D.S3= (S1+S2)
A
2
知识点
两平行线之间的距离
1.定义:两条平行线中,一条直线上任一点到另一条
直线的距离,叫做这两条平行线之间的距离;
2.性质:如果两条直线平行,则其中一条直线上任意
两点到另一条直线的距离相等,即:平行线间的距
离处处相等.
例4 .如图6-16,在平行四边形ABCD中,点M、N分别是AD、BC上的两点,点E、F在对角线BD上,且DM=BN,BE=DF.
求证:四边形MENF是平行四边形.
证明: ∵四边形ABCD是平行四边形
∴AD∥CB
∴∠MDF=∠NBE
∵DM=BN DF=BE
∴△MDF≌△NBE
∴MF=EN ∠MFD=∠NEB
∴∠MFE=∠NEF
∴MF∥EN
∴四边形MENF是平行四边形
练习
如图,已知a∥b,AB∥CD,CE⊥b,FG⊥b,点E,
G为垂足,则下列结论中错误的是( )
A.AB=CD
B.CE=FG
C.A,B两点间的距离就
是线段AB的长
D.直线a,b间的距离就
是线段CD的长
导引:
根据“两点间的距离”,“两平行线间的距离”
的有关概念和定理,可以作出判断.
D
练习
如图,已知直线a∥b,点A,E,F在直线a上,
点B,C,D在直线b上,BC=EF. △ABC与△DEF的面积相等吗?为什么?
△ABC和△DEF的面积相等.理由如下:
如图,作AH1⊥直线b,垂足为点H1,
作DH2⊥直线a,垂足为点H2.
设△ABC和△DEF的面积分别为S1和S2,
∴S1= BC·AH1,
S2= EF·DH2.
∵直线a∥b,AH1⊥直线b,
DH2⊥直线a,
∴AH1=DH2.又∵BC=EF,
∴S1=S2,
即△ABC与△DEF的面积相等.
解答本题的关键是找它们是等高这一条件.等
底等高的三角形面积相等.今后可作为定理直接应
用.
总 结
1
如图,a∥b,则直线a与直线b的距离是( )
A.13
B.14
C.17
D.25
A
随堂练习
2
如图,已知l1∥l2,AB∥CD,HE⊥l2,FG⊥l2,垂足分别为E,G,则下列说法错误的是( )
A.AB的长就是l1与l2之间的距离
B.AB=CD
C.HE的长就是l1
与l2之间的距离
D.HE=FG
A
如图,已知AD∥BC,∠ABC的平分线BP与∠BAD的平分线AP相交于点P,作PE⊥AB于点E.若PE=2,求两平行线AD与BC间的距离.
3
过点P作PM⊥AD于M,
延长MP交BC于N,如图所示.
∵PM⊥AD,AD∥BC,∴PN⊥BC.
∵AP平分∠BAD,PE⊥AB,PM⊥AD,∴PM=PE=2.
∵BP平分∠ABC,PE⊥AB,PN⊥BC,∴PN=PE=2.
∴MN=PM+PN=2+2=4.
解:
已知:如图,在?ABCD中,点E在BC的延长线,且DE∥AC.请写出BE与BC的数量关系,并证明你的结论.
4
结论:BE=2BC.
证明如下:∵四边形ABCD为平行四边形,
∴AD=BC,AD∥BC,即AD∥CE.
∵DE∥AC,
∴四边形ADEC为平行四边形.
∴AD=CE.∴CE=BC.
∴BE=2BC.
解:
1. 平行线间的距离:两条平行线中,一条直线上任一
点到另一条直线的距离,叫做这两条平行线之间的
距离;
2. 平行线间的距离的性质:如果两条直线平行,则其
中一条直线上任意两点到另一条直线的距离相等,
即:平行线间的距离处处相等.
1
知识小结
课堂小结
课后习题!
课后作业
1.平行四边形的定义是什么?它有什么作用?
2.平行四边形有哪些判断方法?
导入新课
1
知识点
平行线间的平行线段
在笔直的铁轨上,夹
在两根铁轨之间的平行枕
木是否一样长?你能说明
理由吗?与同伴交流.
感悟新知
例3
已知:如图,直线a∥b,A、B是直线a上任意两点,AC⊥b,BD⊥b,垂足分别为C,D.
求证:AC=BD.
∵AC⊥CD,BD⊥CD,
∴∠1=∠2=90°.
∴AC∥BD.
∵ AB∥CD.
∴四边形ACDB是平行四边形(平行四边形的定义).
∴AC=BD(平行四边形的对边相等).
证明:
数学表达式:
如图,A,C是l1上任意两点,
∵l1∥l2,AB⊥l2,CD⊥l2,
∴AB=CD.
拓展:
(1)夹在两条平行线间的任何平行线段都相等;
(2)等底等高的三角形的面积相等.
1
如图,在?ABCD中,E,F分别为BC,AD边上
的点,要使BF=DE,
需添加一个条件:_______________________.
BF∥DE(答案不唯一)
随堂练习
2
如图,已知l1∥l2,AB∥CD,AD=CE,DE,FG都垂直于l2,E,G分别为垂足,则下列选项中,一定成立的是( )
A.AB=CD
B.CE=FG
C.BC=EG
D.S四边形ABCD>S四边形DEGF
A
3
如图,已知直线a∥b,点A,B,C在直线a上,点D,E,F在直线b上,AB=EF=2,若△CEF的面积为5,则△ABD的面积为( )
A.2
B.4
C.5
D.10
C
4
如图,设点P是?ABCD的边AB上任意一点,设△APD的面积为S1,△BPC的面积为S2,△CDP的面积为S3,则( )
A.S3=S1+S2
B.S3>S1+S2
C.S3<S1+S2
D.S3= (S1+S2)
A
2
知识点
两平行线之间的距离
1.定义:两条平行线中,一条直线上任一点到另一条
直线的距离,叫做这两条平行线之间的距离;
2.性质:如果两条直线平行,则其中一条直线上任意
两点到另一条直线的距离相等,即:平行线间的距
离处处相等.
例4 .如图6-16,在平行四边形ABCD中,点M、N分别是AD、BC上的两点,点E、F在对角线BD上,且DM=BN,BE=DF.
求证:四边形MENF是平行四边形.
证明: ∵四边形ABCD是平行四边形
∴AD∥CB
∴∠MDF=∠NBE
∵DM=BN DF=BE
∴△MDF≌△NBE
∴MF=EN ∠MFD=∠NEB
∴∠MFE=∠NEF
∴MF∥EN
∴四边形MENF是平行四边形
练习
如图,已知a∥b,AB∥CD,CE⊥b,FG⊥b,点E,
G为垂足,则下列结论中错误的是( )
A.AB=CD
B.CE=FG
C.A,B两点间的距离就
是线段AB的长
D.直线a,b间的距离就
是线段CD的长
导引:
根据“两点间的距离”,“两平行线间的距离”
的有关概念和定理,可以作出判断.
D
练习
如图,已知直线a∥b,点A,E,F在直线a上,
点B,C,D在直线b上,BC=EF. △ABC与△DEF的面积相等吗?为什么?
△ABC和△DEF的面积相等.理由如下:
如图,作AH1⊥直线b,垂足为点H1,
作DH2⊥直线a,垂足为点H2.
设△ABC和△DEF的面积分别为S1和S2,
∴S1= BC·AH1,
S2= EF·DH2.
∵直线a∥b,AH1⊥直线b,
DH2⊥直线a,
∴AH1=DH2.又∵BC=EF,
∴S1=S2,
即△ABC与△DEF的面积相等.
解答本题的关键是找它们是等高这一条件.等
底等高的三角形面积相等.今后可作为定理直接应
用.
总 结
1
如图,a∥b,则直线a与直线b的距离是( )
A.13
B.14
C.17
D.25
A
随堂练习
2
如图,已知l1∥l2,AB∥CD,HE⊥l2,FG⊥l2,垂足分别为E,G,则下列说法错误的是( )
A.AB的长就是l1与l2之间的距离
B.AB=CD
C.HE的长就是l1
与l2之间的距离
D.HE=FG
A
如图,已知AD∥BC,∠ABC的平分线BP与∠BAD的平分线AP相交于点P,作PE⊥AB于点E.若PE=2,求两平行线AD与BC间的距离.
3
过点P作PM⊥AD于M,
延长MP交BC于N,如图所示.
∵PM⊥AD,AD∥BC,∴PN⊥BC.
∵AP平分∠BAD,PE⊥AB,PM⊥AD,∴PM=PE=2.
∵BP平分∠ABC,PE⊥AB,PN⊥BC,∴PN=PE=2.
∴MN=PM+PN=2+2=4.
解:
已知:如图,在?ABCD中,点E在BC的延长线,且DE∥AC.请写出BE与BC的数量关系,并证明你的结论.
4
结论:BE=2BC.
证明如下:∵四边形ABCD为平行四边形,
∴AD=BC,AD∥BC,即AD∥CE.
∵DE∥AC,
∴四边形ADEC为平行四边形.
∴AD=CE.∴CE=BC.
∴BE=2BC.
解:
1. 平行线间的距离:两条平行线中,一条直线上任一
点到另一条直线的距离,叫做这两条平行线之间的
距离;
2. 平行线间的距离的性质:如果两条直线平行,则其
中一条直线上任意两点到另一条直线的距离相等,
即:平行线间的距离处处相等.
1
知识小结
课堂小结
课后习题!
课后作业
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
