北师大版数学七年级下册2.4用尺规作角习题课件(共28张PPT)
文档属性
| 名称 | 北师大版数学七年级下册2.4用尺规作角习题课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 483.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-18 14:32:51 | ||
图片预览



文档简介
初中数学(北师大版)
七年级 下册
第二章 相交线与平行线
知识点????用尺规作一个角等于已知角
1.尺规作图的意义
在几何中,只用没有刻度的直尺和圆规作图称为尺规作图.实际上,我们经
常用的是有刻度的直尺和三角板,在严格的尺规作图中,只能用直尺来画直
线,不能用其刻度来度量长度,圆规则用来作圆(或弧)或截取一定长度的线
段.
2.用尺规作一个角等于已知角
尺规作图一般有以下四步:
已知,求作,作法,写出结论.
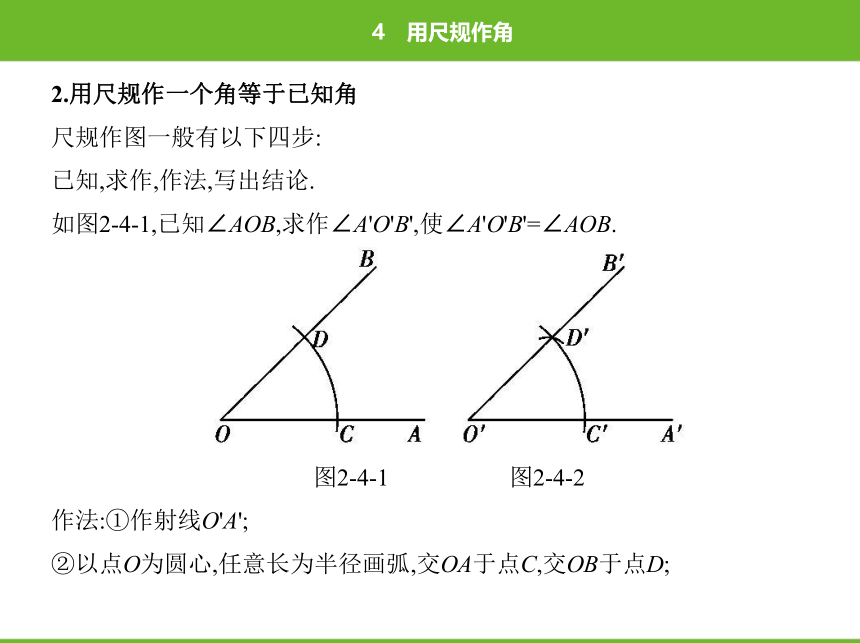
如图2-4-1,已知∠AOB,求作∠A'O'B',使∠A'O'B'=∠AOB.
?
图2-4-1 图2-4-2
作法:①作射线O'A';
②以点O为圆心,任意长为半径画弧,交OA于点C,交OB于点D;
③以点O'为圆心,OC长为半径画弧,交O'A'于点C';
④以点C'为圆心,CD长为半径画弧,交前面的弧于点D';
⑤过点D'作射线O'B',则∠A'O'B'就是所求作的角,如图2-4-2.
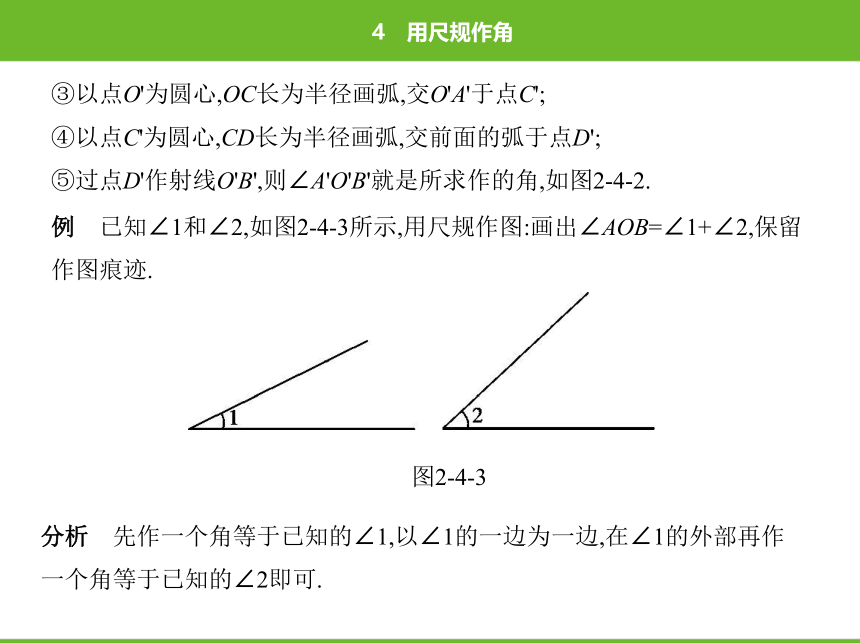
例 已知∠1和∠2,如图2-4-3所示,用尺规作图:画出∠AOB=∠1+∠2,保留
作图痕迹.
?
图2-4-3
分析 先作一个角等于已知的∠1,以∠1的一边为一边,在∠1的外部再作
一个角等于已知的∠2即可.
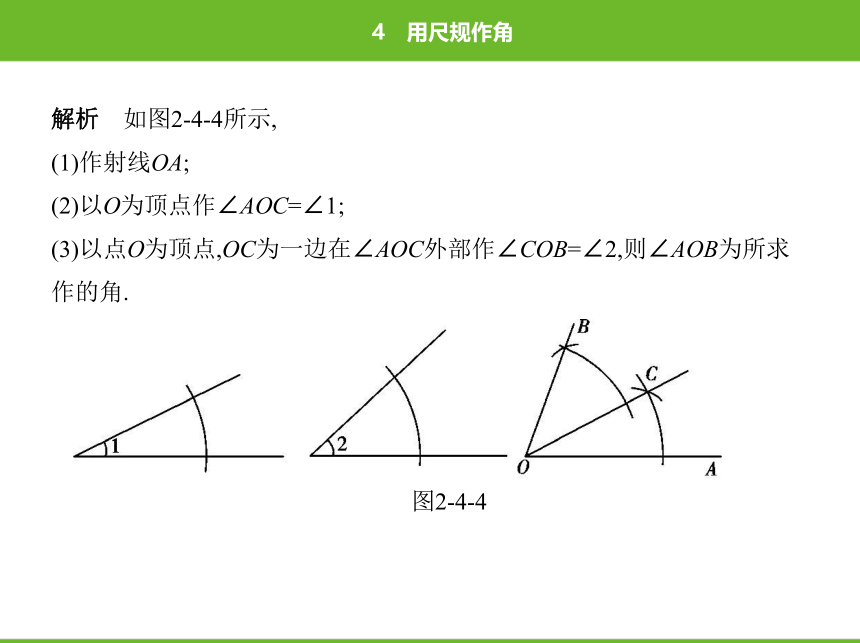
解析 如图2-4-4所示,
(1)作射线OA;
(2)以O为顶点作∠AOC=∠1;
(3)以点O为顶点,OC为一边在∠AOC外部作∠COB=∠2,则∠AOB为所求
作的角.
?
图2-4-4
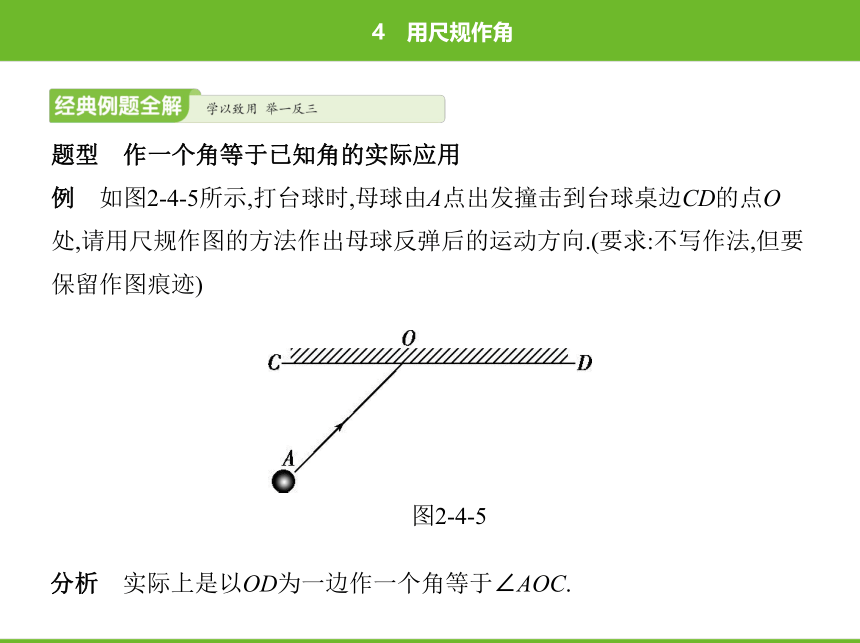
题型????作一个角等于已知角的实际应用
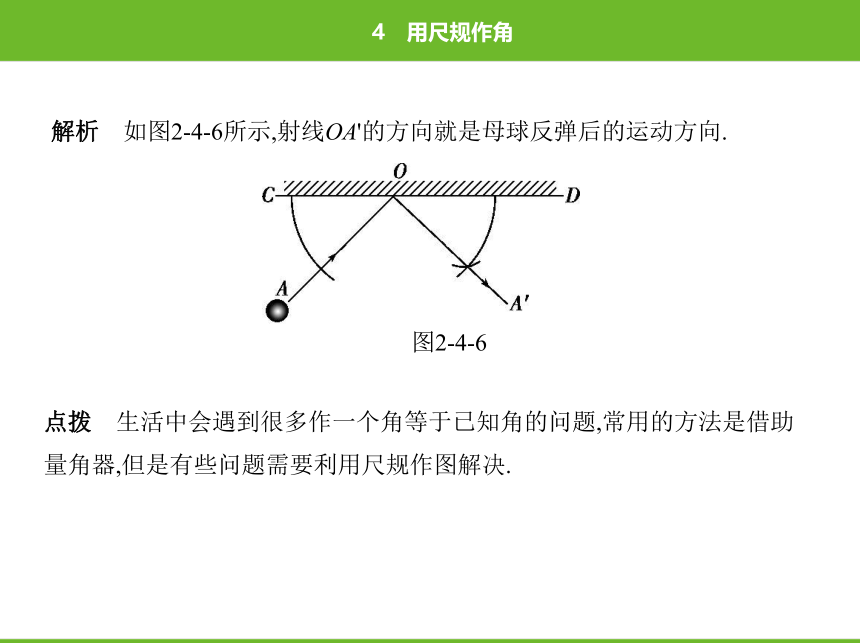
例 如图2-4-5所示,打台球时,母球由A点出发撞击到台球桌边CD的点O
处,请用尺规作图的方法作出母球反弹后的运动方向.(要求:不写作法,但要
保留作图痕迹)
?
图2-4-5
分析 实际上是以OD为一边作一个角等于∠AOC.
解析 如图2-4-6所示,射线OA'的方向就是母球反弹后的运动方向.
?
图2-4-6
点拨 生活中会遇到很多作一个角等于已知角的问题,常用的方法是借助
量角器,但是有些问题需要利用尺规作图解决.
平行线性质与判定综合运用中的逻辑推理
素养解读 逻辑推理是指从一些事实和命题出发,依据规则推出其他命题
的素养.主要包括两类:一类是从特殊到一般的推理,推理形式主要有归
纳、类比;一类是从一般到特殊的推理,推理形式主要有演绎.
逻辑推理是得到数学结论、构建数学体系的重要方式,是数学严谨性的基
本保证,是人们在数学活动中进行交流的基本思维品质.
在逻辑推理核心素养的形成过程中,学生能掌握逻辑推理的基本形式,学会
有逻辑地思考问题;能够在比较复杂的情境中把握事物之间的关联,把握事
物发展的脉络;形成重论据、有条理、合乎逻辑的思维品质和理性精神,增
强交流能力.
典例剖析
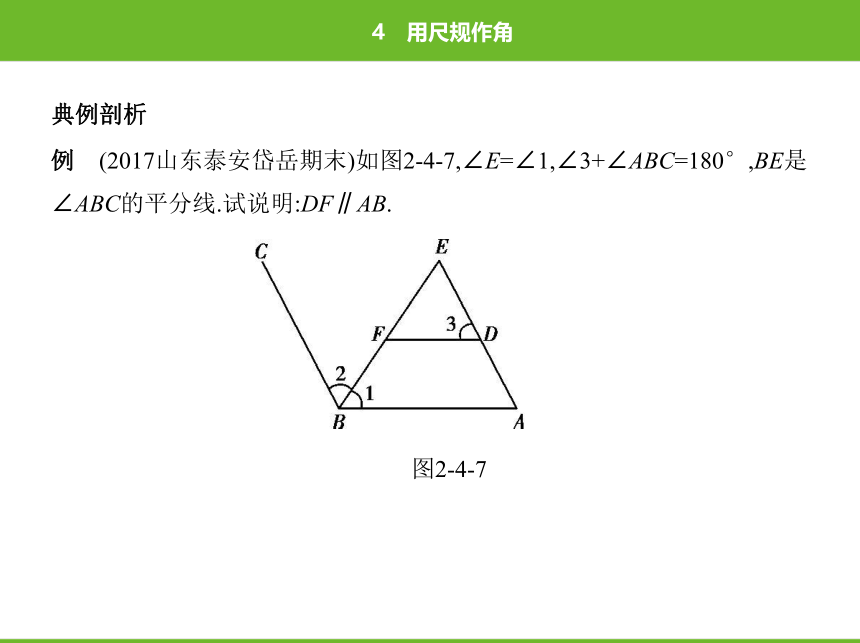
例????(2017山东泰安岱岳期末)如图2-4-7,∠E=∠1,∠3+∠ABC=180°,BE是
∠ABC的平分线.试说明:DF∥AB.
?
图2-4-7
解析 ∵BE是∠ABC的平分线,∴∠1=∠2,
∵∠E=∠1,∴∠E=∠2,
∴AE∥BC,
∴∠A+∠ABC=180°,
∵∠3+∠ABC=180°,
∴∠A=∠3,
∴DF∥AB.
素养呈现 这是一个利用平行线的性质与判定的典型题目,要得到平行,先
说明角的数量关系,要得到角的数量关系,先找平行.由角平分线的性质和
∠E=∠1得到∠E=∠2,进而判定BC与AE平行,再利用平行线的性质得出
∠A与∠ABC互补,再根据∠3与∠ABC互补,得到∠A=∠3,即可得到DF∥AB.
知识点????用尺规作一个角等于已知角
1.下列关于尺规的功能说法不正确的是?( )
A.直尺的功能:在两点间连接一条线段,将线段向两方延长
B.直尺的功能:可作平角和直角
C.圆规的功能:以任意长为半径,任意点为圆心作一个圆
D.圆规的功能:以任意长为半径,任意点为圆心作一段弧
答案????B 尺规作图中的直尺不含单位长度和角度,不能用直尺作直角,直
尺的功能是作直线、射线、线段.
2.下列语句是有关几何作图的叙述.
①以O为圆心作弧;②延长射线AB到点C;③作∠AOB,使∠AOB=∠1;④作
直线AB,使AB=a;⑤过三角形ABC的顶点C作它的对边AB的平行线.其中正
确的为 ????(填序号即可).
答案 ③⑤
解析 ①以O为圆心作弧可以画出无数条弧,因为半径不固定,所以叙述错
误;②射线AB是由A向B无限延伸的,所以叙述错误;③根据作一个角等于已
知角的作法,可以作∠AOB,使∠AOB等于∠1,所以叙述正确;④直线可以向
两方无限延伸,所以叙述错误;⑤根据平行公理:过直线外一点有且只有一
条直线与已知直线平行,知可以过三角形ABC的顶点C作它的对边AB的平
行线,所以叙述正确.所以正确的为③⑤.
3.我们都知道,光照射到镜面会被反射出去,光的反射是有规律的.如图2-4-
1,BC为镜面,AO为入射光线,过点O与镜面垂直的线叫法线,入射光线与法
线的夹角叫入射角,反射光线与法线的夹角叫反射角,反射的规律就是反射
角等于入射角,你能在图中作出反射光线吗?
?
图2-4-1
解析 以点O为顶点作∠DOC=∠AOB(OD与OA在BC的同侧),射线OD就
是反射光线,作图略.
1.下列作图属于尺规作图的是?( )
A.用量角器画出∠AOB的平分线OC
B.已知∠α,作∠AOB,使∠AOB=2∠α
C.用刻度尺画线段AB=3 cm
D.用三角板过点P作AB的垂线
答案????B 只用没有刻度的直尺和圆规作图称为尺规作图.
2.如图所示,已知∠α,∠β(∠β>∠α),求作一个角,使它等于∠β与∠α的差.
?
解析 作∠COB=∠β,在∠β的内部以OB为一边,作∠AOB=∠α,则∠AOC
就是所要求作的角,如图所示.
??????
1.补充作法:
已知:∠AOB,如图2-4-2①.
求作:∠A'O'B',使∠A'O'B'=2∠AOB.
作法:如图2-4-2②,
(1)以点O为圆心,以 ????长为半径画弧,与OA交于点A',与OB交于点C;
(2)以点C为圆心,以 ????长为半径画弧,交前弧于点B';
(3)从O点出发过点B‘作 ????,∠A'OB'就是所求作的角(此时O'与O重合).
?
图2-4-2
答案 (1)任意 (2)A'C (3)射线OB'
2.如图2-4-3,利用尺规,在△ABC的边AC上方作∠CAE=∠ACB,在射线AE上
截取AD=BC,连接CD.(尺规作图,要求保留作图痕迹,不写作法)
?
图2-4-3
解析 如图所示.
?
如图,已知∠AOB及其两边上的点C,D,过点C作CE∥OB,过点D作DF∥
OA,使CE,DF交于点P.
?
?
解析 如图,作∠ACE=∠O,∠BDF=∠O即可,作图痕迹略.
解答题
(2019河北保定十七中期中,29,★★☆)如图2-4-4甲,OA⊥OB,OC⊥OD.
(1)∠AOC与∠BOD有何数量关系?依据是什么?
(2)小明做完(1)后受到启发,在图2-4-4乙中用尺规作出了OD⊥OC,请你也
试一试.
?
图2-4-4
解析 (1)∠AOC=∠BOD.
依据是同角的余角相等.
(2)如图(在∠AOB外部作∠BOD=∠AOC即可).
?
(2018甘肃景泰四中期中,23,★☆☆)作图题.(不写作法,保留作图痕迹)
已知∠α(如图).请你用直尺和圆规画∠BAC,使∠BAC=∠α.
?????
解析 ∠BAC为所求作的角.
选择题
1.(2017湖北宜昌中考,4,★☆☆)谜语:干活两腿脚,一腿勤,一腿懒,一脚站,
一脚转.打一数学学习工具,谜底为?( )
A.量角器 ????B.直尺 ????C.三角板 ????D.圆规
答案????D 圆规有两只脚,一只脚固定,另一只脚旋转.
2.(2017广西南宁中考,7,★☆☆)如图2-4-5,△ABC中,AB>AC,观察图中尺规
作图的痕迹,则下列结论错误的是?( )
?
图2-4-5
A.∠DAE=∠B ????B.∠EAC=∠C
C.AE∥BC ??? ?D.∠DAE=∠EAC
答案????D????根据作图痕迹可知,题图是用尺规作一个角等于已知角,即
∠DAE=∠B,进而得到AE∥BC,从而有∠EAC=∠C,故选项A、B、C中
结论均正确,应用排除法,知选D.
(2017湖北随州中考,6,★☆☆)如图,用尺规作图作∠AOC=∠AOB的第一步
是以点O为圆心,以任意长为半径画弧①,分别交OA、OB于点E、F,那么第
二步的作图痕迹②的作法是?( )
?
A.以点F为圆心,OE长为半径画弧 B.以点F为圆心,EF长为半径画弧
C.以点E为圆心,OE长为半径画弧 D.以点E为圆心,EF长为半径画弧
答案????D????
如图2-4-6所示,用尺规作出∠OBF=∠AOB,作图痕迹弧MN是?( )
?
图2-4-6
A.以点B为圆心,OD长为半径的弧
B.以点B为圆心,OC长为半径的弧
C.以点E为圆心,OD长为半径的弧
D.以点E为圆心,DC长为半径的弧
分别交射线OA,OB于点C,D;②以点B为圆心,以OC长为半径画弧,交BO于
点E;③以点E为圆心,以CD长为半径画弧,交前弧于点F,过点F作射线BF,即
可得到∠OBF,则∠OBF=∠AOB.由此可知选D.
答案????D 作∠OBF=∠AOB的作法:①以点O为圆心,任意长为半径画弧,
根据要求,用尺规作图.(不写作法,只需保留作图痕迹)如图,在AD的右侧
作∠DCP=∠DAB.
?
?
解析 如图.
七年级 下册
第二章 相交线与平行线
知识点????用尺规作一个角等于已知角
1.尺规作图的意义
在几何中,只用没有刻度的直尺和圆规作图称为尺规作图.实际上,我们经
常用的是有刻度的直尺和三角板,在严格的尺规作图中,只能用直尺来画直
线,不能用其刻度来度量长度,圆规则用来作圆(或弧)或截取一定长度的线
段.
2.用尺规作一个角等于已知角
尺规作图一般有以下四步:
已知,求作,作法,写出结论.
如图2-4-1,已知∠AOB,求作∠A'O'B',使∠A'O'B'=∠AOB.
?
图2-4-1 图2-4-2
作法:①作射线O'A';
②以点O为圆心,任意长为半径画弧,交OA于点C,交OB于点D;
③以点O'为圆心,OC长为半径画弧,交O'A'于点C';
④以点C'为圆心,CD长为半径画弧,交前面的弧于点D';
⑤过点D'作射线O'B',则∠A'O'B'就是所求作的角,如图2-4-2.
例 已知∠1和∠2,如图2-4-3所示,用尺规作图:画出∠AOB=∠1+∠2,保留
作图痕迹.
?
图2-4-3
分析 先作一个角等于已知的∠1,以∠1的一边为一边,在∠1的外部再作
一个角等于已知的∠2即可.
解析 如图2-4-4所示,
(1)作射线OA;
(2)以O为顶点作∠AOC=∠1;
(3)以点O为顶点,OC为一边在∠AOC外部作∠COB=∠2,则∠AOB为所求
作的角.
?
图2-4-4
题型????作一个角等于已知角的实际应用
例 如图2-4-5所示,打台球时,母球由A点出发撞击到台球桌边CD的点O
处,请用尺规作图的方法作出母球反弹后的运动方向.(要求:不写作法,但要
保留作图痕迹)
?
图2-4-5
分析 实际上是以OD为一边作一个角等于∠AOC.
解析 如图2-4-6所示,射线OA'的方向就是母球反弹后的运动方向.
?
图2-4-6
点拨 生活中会遇到很多作一个角等于已知角的问题,常用的方法是借助
量角器,但是有些问题需要利用尺规作图解决.
平行线性质与判定综合运用中的逻辑推理
素养解读 逻辑推理是指从一些事实和命题出发,依据规则推出其他命题
的素养.主要包括两类:一类是从特殊到一般的推理,推理形式主要有归
纳、类比;一类是从一般到特殊的推理,推理形式主要有演绎.
逻辑推理是得到数学结论、构建数学体系的重要方式,是数学严谨性的基
本保证,是人们在数学活动中进行交流的基本思维品质.
在逻辑推理核心素养的形成过程中,学生能掌握逻辑推理的基本形式,学会
有逻辑地思考问题;能够在比较复杂的情境中把握事物之间的关联,把握事
物发展的脉络;形成重论据、有条理、合乎逻辑的思维品质和理性精神,增
强交流能力.
典例剖析
例????(2017山东泰安岱岳期末)如图2-4-7,∠E=∠1,∠3+∠ABC=180°,BE是
∠ABC的平分线.试说明:DF∥AB.
?
图2-4-7
解析 ∵BE是∠ABC的平分线,∴∠1=∠2,
∵∠E=∠1,∴∠E=∠2,
∴AE∥BC,
∴∠A+∠ABC=180°,
∵∠3+∠ABC=180°,
∴∠A=∠3,
∴DF∥AB.
素养呈现 这是一个利用平行线的性质与判定的典型题目,要得到平行,先
说明角的数量关系,要得到角的数量关系,先找平行.由角平分线的性质和
∠E=∠1得到∠E=∠2,进而判定BC与AE平行,再利用平行线的性质得出
∠A与∠ABC互补,再根据∠3与∠ABC互补,得到∠A=∠3,即可得到DF∥AB.
知识点????用尺规作一个角等于已知角
1.下列关于尺规的功能说法不正确的是?( )
A.直尺的功能:在两点间连接一条线段,将线段向两方延长
B.直尺的功能:可作平角和直角
C.圆规的功能:以任意长为半径,任意点为圆心作一个圆
D.圆规的功能:以任意长为半径,任意点为圆心作一段弧
答案????B 尺规作图中的直尺不含单位长度和角度,不能用直尺作直角,直
尺的功能是作直线、射线、线段.
2.下列语句是有关几何作图的叙述.
①以O为圆心作弧;②延长射线AB到点C;③作∠AOB,使∠AOB=∠1;④作
直线AB,使AB=a;⑤过三角形ABC的顶点C作它的对边AB的平行线.其中正
确的为 ????(填序号即可).
答案 ③⑤
解析 ①以O为圆心作弧可以画出无数条弧,因为半径不固定,所以叙述错
误;②射线AB是由A向B无限延伸的,所以叙述错误;③根据作一个角等于已
知角的作法,可以作∠AOB,使∠AOB等于∠1,所以叙述正确;④直线可以向
两方无限延伸,所以叙述错误;⑤根据平行公理:过直线外一点有且只有一
条直线与已知直线平行,知可以过三角形ABC的顶点C作它的对边AB的平
行线,所以叙述正确.所以正确的为③⑤.
3.我们都知道,光照射到镜面会被反射出去,光的反射是有规律的.如图2-4-
1,BC为镜面,AO为入射光线,过点O与镜面垂直的线叫法线,入射光线与法
线的夹角叫入射角,反射光线与法线的夹角叫反射角,反射的规律就是反射
角等于入射角,你能在图中作出反射光线吗?
?
图2-4-1
解析 以点O为顶点作∠DOC=∠AOB(OD与OA在BC的同侧),射线OD就
是反射光线,作图略.
1.下列作图属于尺规作图的是?( )
A.用量角器画出∠AOB的平分线OC
B.已知∠α,作∠AOB,使∠AOB=2∠α
C.用刻度尺画线段AB=3 cm
D.用三角板过点P作AB的垂线
答案????B 只用没有刻度的直尺和圆规作图称为尺规作图.
2.如图所示,已知∠α,∠β(∠β>∠α),求作一个角,使它等于∠β与∠α的差.
?
解析 作∠COB=∠β,在∠β的内部以OB为一边,作∠AOB=∠α,则∠AOC
就是所要求作的角,如图所示.
??????
1.补充作法:
已知:∠AOB,如图2-4-2①.
求作:∠A'O'B',使∠A'O'B'=2∠AOB.
作法:如图2-4-2②,
(1)以点O为圆心,以 ????长为半径画弧,与OA交于点A',与OB交于点C;
(2)以点C为圆心,以 ????长为半径画弧,交前弧于点B';
(3)从O点出发过点B‘作 ????,∠A'OB'就是所求作的角(此时O'与O重合).
?
图2-4-2
答案 (1)任意 (2)A'C (3)射线OB'
2.如图2-4-3,利用尺规,在△ABC的边AC上方作∠CAE=∠ACB,在射线AE上
截取AD=BC,连接CD.(尺规作图,要求保留作图痕迹,不写作法)
?
图2-4-3
解析 如图所示.
?
如图,已知∠AOB及其两边上的点C,D,过点C作CE∥OB,过点D作DF∥
OA,使CE,DF交于点P.
?
?
解析 如图,作∠ACE=∠O,∠BDF=∠O即可,作图痕迹略.
解答题
(2019河北保定十七中期中,29,★★☆)如图2-4-4甲,OA⊥OB,OC⊥OD.
(1)∠AOC与∠BOD有何数量关系?依据是什么?
(2)小明做完(1)后受到启发,在图2-4-4乙中用尺规作出了OD⊥OC,请你也
试一试.
?
图2-4-4
解析 (1)∠AOC=∠BOD.
依据是同角的余角相等.
(2)如图(在∠AOB外部作∠BOD=∠AOC即可).
?
(2018甘肃景泰四中期中,23,★☆☆)作图题.(不写作法,保留作图痕迹)
已知∠α(如图).请你用直尺和圆规画∠BAC,使∠BAC=∠α.
?????
解析 ∠BAC为所求作的角.
选择题
1.(2017湖北宜昌中考,4,★☆☆)谜语:干活两腿脚,一腿勤,一腿懒,一脚站,
一脚转.打一数学学习工具,谜底为?( )
A.量角器 ????B.直尺 ????C.三角板 ????D.圆规
答案????D 圆规有两只脚,一只脚固定,另一只脚旋转.
2.(2017广西南宁中考,7,★☆☆)如图2-4-5,△ABC中,AB>AC,观察图中尺规
作图的痕迹,则下列结论错误的是?( )
?
图2-4-5
A.∠DAE=∠B ????B.∠EAC=∠C
C.AE∥BC ??? ?D.∠DAE=∠EAC
答案????D????根据作图痕迹可知,题图是用尺规作一个角等于已知角,即
∠DAE=∠B,进而得到AE∥BC,从而有∠EAC=∠C,故选项A、B、C中
结论均正确,应用排除法,知选D.
(2017湖北随州中考,6,★☆☆)如图,用尺规作图作∠AOC=∠AOB的第一步
是以点O为圆心,以任意长为半径画弧①,分别交OA、OB于点E、F,那么第
二步的作图痕迹②的作法是?( )
?
A.以点F为圆心,OE长为半径画弧 B.以点F为圆心,EF长为半径画弧
C.以点E为圆心,OE长为半径画弧 D.以点E为圆心,EF长为半径画弧
答案????D????
如图2-4-6所示,用尺规作出∠OBF=∠AOB,作图痕迹弧MN是?( )
?
图2-4-6
A.以点B为圆心,OD长为半径的弧
B.以点B为圆心,OC长为半径的弧
C.以点E为圆心,OD长为半径的弧
D.以点E为圆心,DC长为半径的弧
分别交射线OA,OB于点C,D;②以点B为圆心,以OC长为半径画弧,交BO于
点E;③以点E为圆心,以CD长为半径画弧,交前弧于点F,过点F作射线BF,即
可得到∠OBF,则∠OBF=∠AOB.由此可知选D.
答案????D 作∠OBF=∠AOB的作法:①以点O为圆心,任意长为半径画弧,
根据要求,用尺规作图.(不写作法,只需保留作图痕迹)如图,在AD的右侧
作∠DCP=∠DAB.
?
?
解析 如图.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
