初中数学北师大版七年级下册3.2用关系式表示变量之间的关系课件 (共21张PPT)
文档属性
| 名称 | 初中数学北师大版七年级下册3.2用关系式表示变量之间的关系课件 (共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-18 00:00:00 | ||
图片预览







文档简介
用关系式表示
变量之间的关系
第三章 变量之间的关系
目录
学习指南
知识管理
归类探究
当堂测评
教学目标
1.能根据具体情景,用关系式表示变量间的关系,根据关系式解决相关问题;(重点)
2.并会根据关系式求值,初步体会自变量和因变量的数值对应关系;(重点)
3.通过动手实践与探索,让学生参与变量的发现和函数概念的形成过程,提高分析问题和解决问题的能力.(难点)
学习指南
知识点????用关系式表示两变量之间的关系
1.表示自变量与因变量之间关系的数学式子叫做关系式.关系式是表示变量之间关系的另一种方法.
2.利用关系式,我们可以根据任意一个自变量的值求出对应的因变量的值,也可以根据已知的因变量的值通过解方程求自变量的值.
3.两个变量之间关系式的特征.
(1)关系式是等量,其中等式左边是因变量,右边是含自变量的代数式.
(2)关系式中只含有自变量和因变量这两个变量,其他的量都是常量.
(3)自变量可以在允许的范围内任意取值.
4.用表格和关系式表示两个变量之间的关系有各自的优缺点.用关系式表示变量之间的关系简洁明了,便于分析计算,但需要通过计算才能得到所需结果;表格能直接得到某些具体的对应值,但不能反映变量的整体变化情况.
知识管理
如图,三角形ABC底边BC上的高是6厘米.当三角形的顶点C沿底边所在的直线向点B运动时,三角形的面积发生了怎样的变化?
(1)在这个变化过程中,自变量和因变量分别是什么?
三角形的底边长度是自变量,三角形的面积是因变量.
(2)如果三角形的底边长为x(厘米),那么三角形的面积y(厘米2)可以表示为________.
(3)当底边长从12厘米变化到3厘米时,三角形的面积从_____厘米2变化到_____厘米2.
类型一:用关系式表示图形中的变量关系
归类探究
归纳总结
y=3x表示了三角形面积和三角形底边长之间的关系,它是变量y随x变化的关系式.
注意:关系式是我们表示变量之间关系的另一种方法,
利用关系式,如y=3x,
我们可以根据任何一个自变量值求出相应的因变量的值.
归类探究
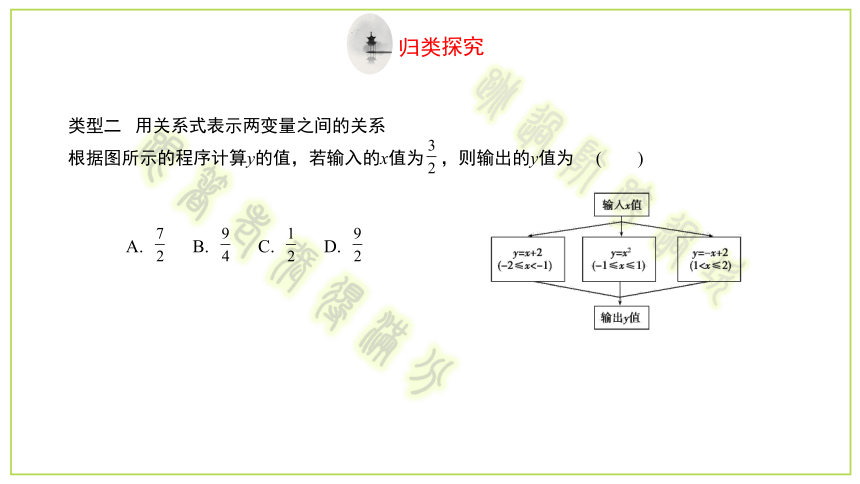
类型二 用关系式表示两变量之间的关系
根据图所示的程序计算y的值,若输入的x值为 ?,则输出的y值为?( )
?
A.? ????B.? ????C.? ????D.?
归类探究
汽车在行驶过程中,由于惯性的作用刹车后仍将滑行一段距离才能停住,这段距离称为刹车距离.刹车距离是分析事故原因的一个重要因素.某型号的汽车在平整路面上的刹车距离sm与车速vkm/h之间有下列经验公式:
(1)式中哪个量是常量?哪个量是变量?哪个量是自变量?哪个量是因变量?
(2)当刹车时车速v 分别是40、80、120km/h时,相应的滑行距离s分别是多少?
当v=40km/h时,s=6.25m;
当 v=80km/h时, s=25m;
当 v=120km/h时,s=56.25m.
归类探究
类型三 用关系式表示所给公式的两变量之间的关系
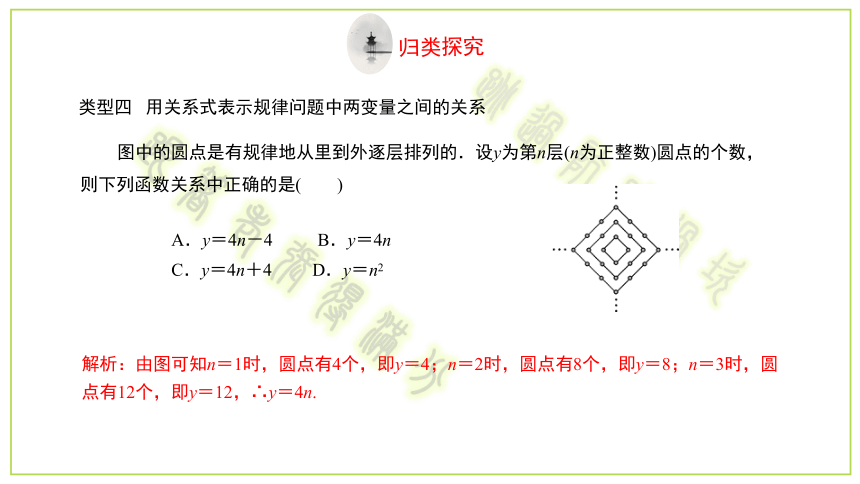
图中的圆点是有规律地从里到外逐层排列的.设y为第n层(n为正整数)圆点的个数,则下列函数关系中正确的是( )
A.y=4n-4 B.y=4n
C.y=4n+4 D.y=n2
解析:由图可知n=1时,圆点有4个,即y=4;n=2时,圆点有8个,即y=8;n=3时,圆点有12个,即y=12,∴y=4n.
归类探究
类型四 用关系式表示规律问题中两变量之间的关系
1.变量x与y之间的关系式是y=x2-3,当自变量x=2时,因变量y的值是( )
A.-2 B.-1 C.1 D.2
【解析】将x=2代入y=x2-3,得y=22-3=1.
同步测评
2.一块长为5米,宽为2米的长方形木板,现要在长边上截取一边长为x米的一小长方形(如图),则剩余木板的面积y(平方米)与x(米)之间的关系式为( )
A.y=2x B.y=10-2x C.y=5x D.y=10-5x
【解析】由题意,有y=2(5-x),即y=10-2x.
同步测评
3.如图是一个简单的数值运算程序,当输入x的值为1时,则输出的数值为____.
4.在关系式S=40t中,当t=1.5时,S=____.
同步测评
5.如图,圆柱的底面直径是2 cm,当圆柱的高h cm由大到小变化时,圆柱的体积V(cm3)随之发生变化.
(1)在这个变化中,自变量和因变量各是什么?
(2)写出圆柱的体积V与高h之间的关系式.
(3)当h由10 cm变化到5 cm时,V是怎样变化的?
(4)当h=0时,V等于多少?此时表示什么?
同步测评
6.对于气温,有的地方用摄氏温度表示,有的地方用华氏温度表示,摄氏
温度x(℃)与华氏温度y(°F)之间存在 的关系为:y=1.8x+32,如图所示:
(1)用表格表示当x从-10到30(每次增加10),y的相应的值.
(2)某天,连云港的最高气温是8℃,悉尼的最高气温是91°F,问这一天悉尼的最高气温比连云港的最高气温高多少摄氏度(结果保留整数)?
(2)y=91,则1.8x+32=91,所以有x≈33,33-8=25(℃).
所以这一天悉尼的最高气温比连云港的高25℃.
同步测评
7.华联超市进了一批玩具,出售时要在进价(进货价格)的基础上加一定的利润,其数量x(个)与售价y(元)如下表:
数量x(个)
1
2
3
4
…
售价y(元)
8+0.3
16+0.6
24+0.9
32+1.2
…
下列用x表示y的关系式中,正确的是?( )
A.y=8x+0.3 ????B.y=(8+0.3)x C.y=8+0.3x ????D.y=8+0.3+x
答案????B 通过观察题表内的x与y,可知y=(8+0.3)x.
同步测评
8.日常生活中,“老人”是一个模糊概念.可用“老人系数”表示一个人的老年化程度.“老人系数”的计算方法如下表:
按照这样的规定,“老人系数”为0.6的人的年龄是 ????岁.
人的年龄x(岁)
x≤60
60x≥80
“老人系数”
0
?
1
同步测评
9.(2018重庆中考B卷)如图所示的程序计算y的值,若输入的x值是4或7时,输出的y值相等,则b等于?( )
A.9 ????B.7 ????C.-9 ????D.-7
同步测评
求变量之间关系式的“三途径”
1.根据表格中所列的数据,归纳总结两个变量的关系式.
2.利用公式写出两个变量之间的关系式,比如各类几何图形的周长、面积、体积公式等.
3.结合实际问题写出两个变量之间的关系式,比如销量×(售价-进价)=利润等.
归纳总结
如图,在R△ABC中,已知∠C=900,边AC=4cm,BC=5cm,点P为CB边上一动点,当点P沿CB从点C向点B运动时,△APC的面积发生了变化。 (1)在这个变化过程中,自变量和因变量各是什么?
(2)如果设CP长为xcm,△APC的面积为ycm2,则y与x的关系可表示为 ;
(3)当点P从点D(点D为BC的中点)运动到点B时,则△APC的面积从 cm2,变到 cm2。
每日拓展
(3)此题中的自变量和因变量分别是什么? (4)写出第n层所对应的点数,以及n层的六边形点阵的总点数; (5)如果某一层的点数是96,它是第几层? (6)有没有一层,它的点数是100?为什么?
如图,是一个形如六边形的点阵,它的中心是一个点,算第一层;第二层每边两个点;第三层每边有三个点,依此类推: (1)填写下表:
{5940675A-B579-460E-94D1-54222C63F5DA}层数
1
2
3
4
5
6
……
该层的点数
……
所有层的点数
……
(2)每层点数是如何随层数的变化而变化的?所有层的总点数是如何随层数的变化而变化的?
每日拓展
变量之间的关系
第三章 变量之间的关系
目录
学习指南
知识管理
归类探究
当堂测评
教学目标
1.能根据具体情景,用关系式表示变量间的关系,根据关系式解决相关问题;(重点)
2.并会根据关系式求值,初步体会自变量和因变量的数值对应关系;(重点)
3.通过动手实践与探索,让学生参与变量的发现和函数概念的形成过程,提高分析问题和解决问题的能力.(难点)
学习指南
知识点????用关系式表示两变量之间的关系
1.表示自变量与因变量之间关系的数学式子叫做关系式.关系式是表示变量之间关系的另一种方法.
2.利用关系式,我们可以根据任意一个自变量的值求出对应的因变量的值,也可以根据已知的因变量的值通过解方程求自变量的值.
3.两个变量之间关系式的特征.
(1)关系式是等量,其中等式左边是因变量,右边是含自变量的代数式.
(2)关系式中只含有自变量和因变量这两个变量,其他的量都是常量.
(3)自变量可以在允许的范围内任意取值.
4.用表格和关系式表示两个变量之间的关系有各自的优缺点.用关系式表示变量之间的关系简洁明了,便于分析计算,但需要通过计算才能得到所需结果;表格能直接得到某些具体的对应值,但不能反映变量的整体变化情况.
知识管理
如图,三角形ABC底边BC上的高是6厘米.当三角形的顶点C沿底边所在的直线向点B运动时,三角形的面积发生了怎样的变化?
(1)在这个变化过程中,自变量和因变量分别是什么?
三角形的底边长度是自变量,三角形的面积是因变量.
(2)如果三角形的底边长为x(厘米),那么三角形的面积y(厘米2)可以表示为________.
(3)当底边长从12厘米变化到3厘米时,三角形的面积从_____厘米2变化到_____厘米2.
类型一:用关系式表示图形中的变量关系
归类探究
归纳总结
y=3x表示了三角形面积和三角形底边长之间的关系,它是变量y随x变化的关系式.
注意:关系式是我们表示变量之间关系的另一种方法,
利用关系式,如y=3x,
我们可以根据任何一个自变量值求出相应的因变量的值.
归类探究
类型二 用关系式表示两变量之间的关系
根据图所示的程序计算y的值,若输入的x值为 ?,则输出的y值为?( )
?
A.? ????B.? ????C.? ????D.?
归类探究
汽车在行驶过程中,由于惯性的作用刹车后仍将滑行一段距离才能停住,这段距离称为刹车距离.刹车距离是分析事故原因的一个重要因素.某型号的汽车在平整路面上的刹车距离sm与车速vkm/h之间有下列经验公式:
(1)式中哪个量是常量?哪个量是变量?哪个量是自变量?哪个量是因变量?
(2)当刹车时车速v 分别是40、80、120km/h时,相应的滑行距离s分别是多少?
当v=40km/h时,s=6.25m;
当 v=80km/h时, s=25m;
当 v=120km/h时,s=56.25m.
归类探究
类型三 用关系式表示所给公式的两变量之间的关系
图中的圆点是有规律地从里到外逐层排列的.设y为第n层(n为正整数)圆点的个数,则下列函数关系中正确的是( )
A.y=4n-4 B.y=4n
C.y=4n+4 D.y=n2
解析:由图可知n=1时,圆点有4个,即y=4;n=2时,圆点有8个,即y=8;n=3时,圆点有12个,即y=12,∴y=4n.
归类探究
类型四 用关系式表示规律问题中两变量之间的关系
1.变量x与y之间的关系式是y=x2-3,当自变量x=2时,因变量y的值是( )
A.-2 B.-1 C.1 D.2
【解析】将x=2代入y=x2-3,得y=22-3=1.
同步测评
2.一块长为5米,宽为2米的长方形木板,现要在长边上截取一边长为x米的一小长方形(如图),则剩余木板的面积y(平方米)与x(米)之间的关系式为( )
A.y=2x B.y=10-2x C.y=5x D.y=10-5x
【解析】由题意,有y=2(5-x),即y=10-2x.
同步测评
3.如图是一个简单的数值运算程序,当输入x的值为1时,则输出的数值为____.
4.在关系式S=40t中,当t=1.5时,S=____.
同步测评
5.如图,圆柱的底面直径是2 cm,当圆柱的高h cm由大到小变化时,圆柱的体积V(cm3)随之发生变化.
(1)在这个变化中,自变量和因变量各是什么?
(2)写出圆柱的体积V与高h之间的关系式.
(3)当h由10 cm变化到5 cm时,V是怎样变化的?
(4)当h=0时,V等于多少?此时表示什么?
同步测评
6.对于气温,有的地方用摄氏温度表示,有的地方用华氏温度表示,摄氏
温度x(℃)与华氏温度y(°F)之间存在 的关系为:y=1.8x+32,如图所示:
(1)用表格表示当x从-10到30(每次增加10),y的相应的值.
(2)某天,连云港的最高气温是8℃,悉尼的最高气温是91°F,问这一天悉尼的最高气温比连云港的最高气温高多少摄氏度(结果保留整数)?
(2)y=91,则1.8x+32=91,所以有x≈33,33-8=25(℃).
所以这一天悉尼的最高气温比连云港的高25℃.
同步测评
7.华联超市进了一批玩具,出售时要在进价(进货价格)的基础上加一定的利润,其数量x(个)与售价y(元)如下表:
数量x(个)
1
2
3
4
…
售价y(元)
8+0.3
16+0.6
24+0.9
32+1.2
…
下列用x表示y的关系式中,正确的是?( )
A.y=8x+0.3 ????B.y=(8+0.3)x C.y=8+0.3x ????D.y=8+0.3+x
答案????B 通过观察题表内的x与y,可知y=(8+0.3)x.
同步测评
8.日常生活中,“老人”是一个模糊概念.可用“老人系数”表示一个人的老年化程度.“老人系数”的计算方法如下表:
按照这样的规定,“老人系数”为0.6的人的年龄是 ????岁.
人的年龄x(岁)
x≤60
60
“老人系数”
0
?
1
同步测评
9.(2018重庆中考B卷)如图所示的程序计算y的值,若输入的x值是4或7时,输出的y值相等,则b等于?( )
A.9 ????B.7 ????C.-9 ????D.-7
同步测评
求变量之间关系式的“三途径”
1.根据表格中所列的数据,归纳总结两个变量的关系式.
2.利用公式写出两个变量之间的关系式,比如各类几何图形的周长、面积、体积公式等.
3.结合实际问题写出两个变量之间的关系式,比如销量×(售价-进价)=利润等.
归纳总结
如图,在R△ABC中,已知∠C=900,边AC=4cm,BC=5cm,点P为CB边上一动点,当点P沿CB从点C向点B运动时,△APC的面积发生了变化。 (1)在这个变化过程中,自变量和因变量各是什么?
(2)如果设CP长为xcm,△APC的面积为ycm2,则y与x的关系可表示为 ;
(3)当点P从点D(点D为BC的中点)运动到点B时,则△APC的面积从 cm2,变到 cm2。
每日拓展
(3)此题中的自变量和因变量分别是什么? (4)写出第n层所对应的点数,以及n层的六边形点阵的总点数; (5)如果某一层的点数是96,它是第几层? (6)有没有一层,它的点数是100?为什么?
如图,是一个形如六边形的点阵,它的中心是一个点,算第一层;第二层每边两个点;第三层每边有三个点,依此类推: (1)填写下表:
{5940675A-B579-460E-94D1-54222C63F5DA}层数
1
2
3
4
5
6
……
该层的点数
……
所有层的点数
……
(2)每层点数是如何随层数的变化而变化的?所有层的总点数是如何随层数的变化而变化的?
每日拓展
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
