北师大版七年级下册数学 6.3等可能事件的概率课件 (共28张PPT)
文档属性
| 名称 | 北师大版七年级下册数学 6.3等可能事件的概率课件 (共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 638.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-18 00:00:00 | ||
图片预览





文档简介
等可能事件的概率(一)
第1课时 与摸球相关的等可能事件的概率
教学目标
一、了解可化为古典概型的几何概型的特点,会根据试验结果的对称性或均衡性判断试验结果是否具有等可能性;
二、掌握古典概型的概率计算方法;
三、能设计符合要求的简单概率模型,初步体会概率是描述不确定现象的数学模型。
设一个实验的所有可能结果有n个,每次
试验有且只有其中的一个结果出现。如果
每个结果出现的可能性相同,那么我们就
称这个试验的结果是等可能的。这个实验
就是一个等可能事件。
袋子里装有两个球,它们除颜色外完全相同。从袋中任意摸出一球.
1.若袋中两个都是红球,摸出一个为红球,称为
事件;摸出一个为白球,称为 事件(选填“必然”“不确定”或“不可能”);
必然
不可能
2.若袋中一个为红球,一个为白球,摸出一个为红球,称为 事件.
不确定
导入新课
复习引入
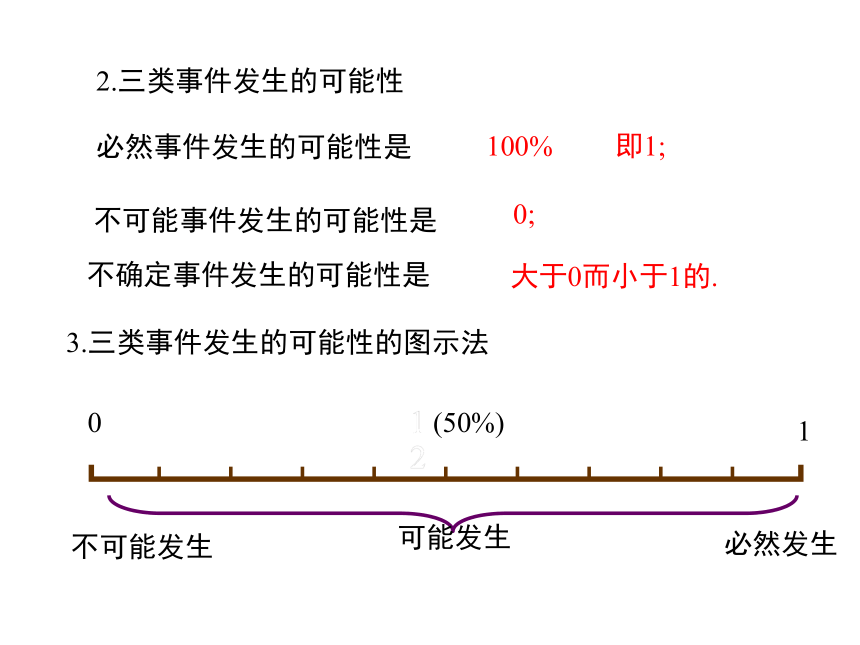
必然事件发生的可能性是
100%
即1;
不可能事件发生的可能性是
0;
大于0而小于1的.
不确定事件发生的可能性是
2.三类事件发生的可能性
不可能发生
3.三类事件发生的可能性的图示法
0
1
(50%)
必然发生
可能发生
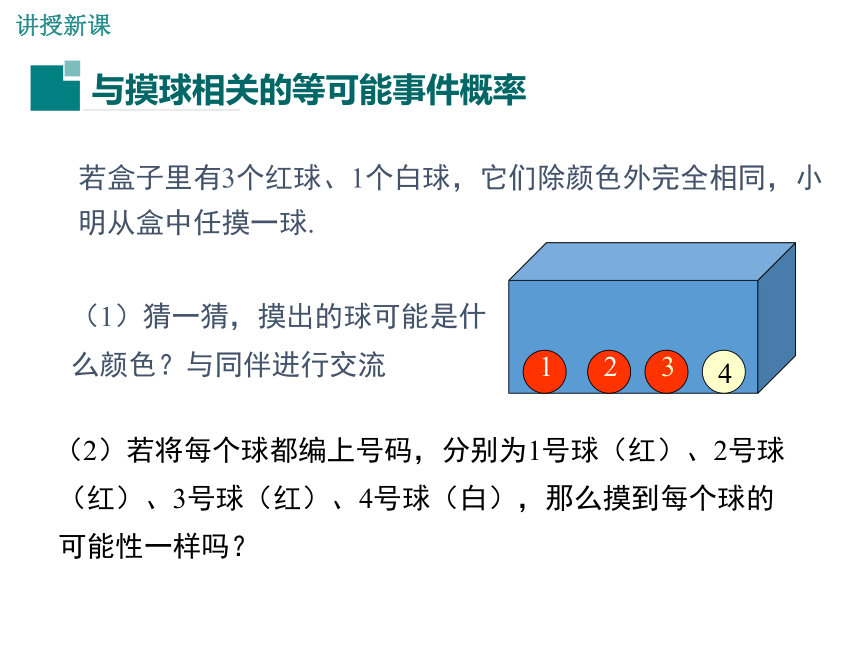
若盒子里有3个红球、1个白球,它们除颜色外完全相同,小明从盒中任摸一球.
2
3
4
1
(2)若将每个球都编上号码,分别为1号球(红)、2号球(红)、3号球(红)、4号球(白),那么摸到每个球的可能性一样吗?
(1)猜一猜,摸出的球可能是什么颜色?与同伴进行交流
讲授新课
与摸球相关的等可能事件概率
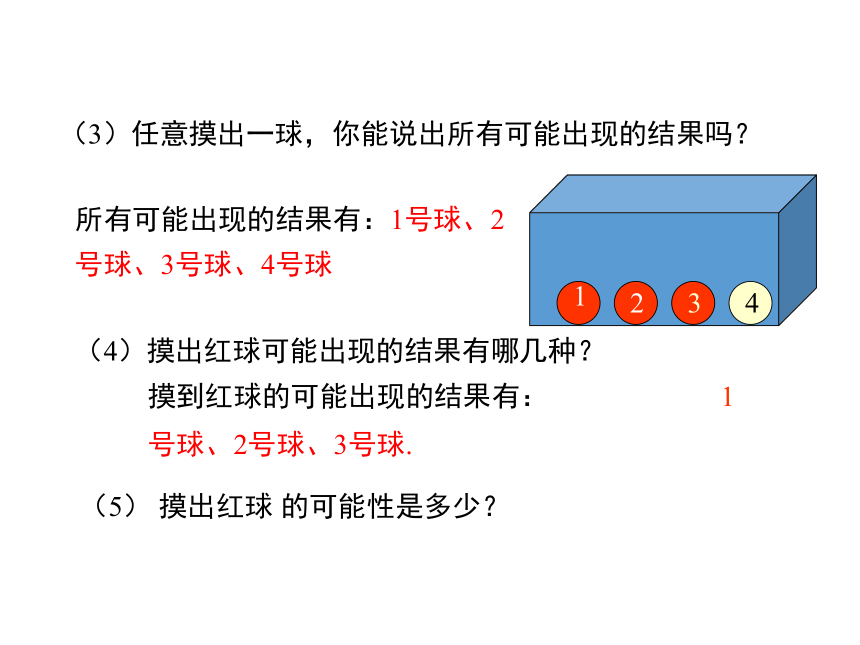
(3)任意摸出一球,你能说出所有可能出现的结果吗?
摸到红球的可能出现的结果有: 1号球、2号球、3号球.
1
2
3
4
1
(4)摸出红球可能出现的结果有哪几种?
所有可能出现的结果有:1号球、2号球、3号球、4号球
(5) 摸出红球 的可能性是多少?
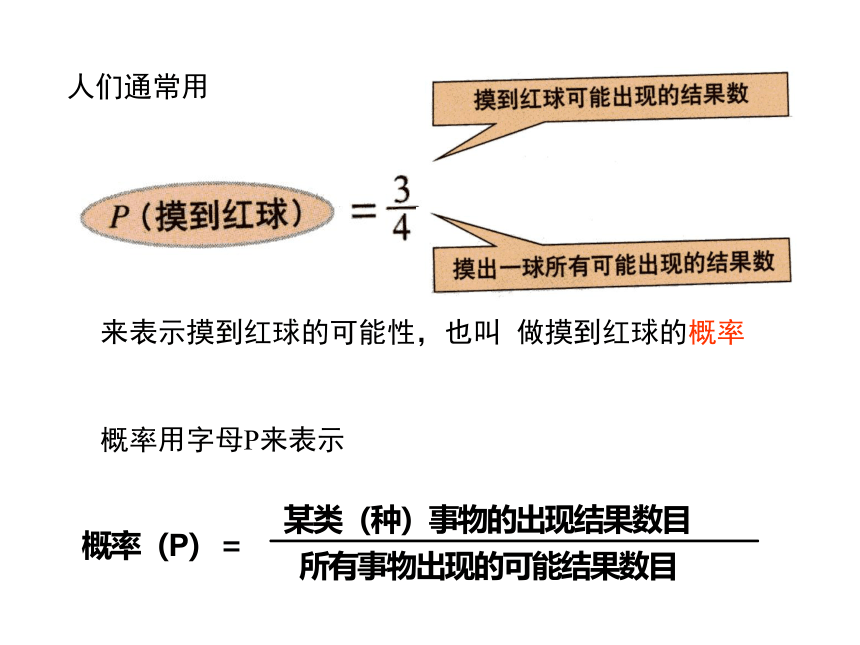
人们通常用
来表示摸到红球的可能性,也叫 做摸到红球的概率
概率用字母P来表示
★ 必然事件发生的概率为
1
记作: P(必然事件)=1;
0
记作: P(不可能事件)=0;
0<P(A) < 1
★ 不可能事件发生的概率为
★ 如果A为不确定事件,那么:
三类事件发生的概率及表示
1、从分别标有1、2、3、4、5号的5个球中随机抽取一个球,抽出的号码有 种可能,
即可能摸到 ,由于这5个球的形状、大小相同,又是随机抽取的,所以我们认为:每个号码抽到的可能性 ,都是 。
2、抛一枚硬币,向上的面有 种可能,即可能抛出 ,由于硬币的构造、质地均匀,又是随机掷出的,所以我们断言:每种结果的可能性 ,都是 。
正面朝上,反面朝上
1号球,2号球,3号球,4号球,5号球
相同
相同
5
2
探索新知
①所有可能的结果是可数的
共同点:
②每种结果出现的可能性相同
A
n
m
m
n
P(A)= —
例如:一副完整的扑克牌54张,抽到A的概率?
P(抽到A)=
一般地,如果一个试验有n个等可能的结果,
事件A包含其中的m个结果,那么事件A发生的
概率为:
P(A)=
所有可能发生的结果数n
事件A发生的结果数m
(1)掷出的点数大于4的结果只有2种:
掷出的点数分别是5,6.所以
P(掷出的点数大于4)= — = —
例:任意掷一枚均匀骰子。
(1)掷出的点数大于4的概率是多少?
解析:任意掷一枚均匀骰子,所有可能的
结果有6种:掷出的点数分别是1,2,3,4,
5,6,因为骰子是均匀的,所以每种结果
出现的可能性相等。
2
6
1
3
规范作答
P(掷出的点数是偶数)= — = —
(2)掷出的点数是偶数的概率是多少?
掷出的点数是偶数的结果有3种:
掷出的点数分别是2,4,6.所以
6
3
2
1
1、一个袋中有3个红球和5个白球,每个球除颜色外都相同。从中任意摸出一球。
①摸到红球和摸到白球的概率相等吗?
②如果不等,能否通过改变袋中红球或白球的数量,使摸到的红球和白球的概率相等?
摸到红球和白球的概率不等
P(摸到红球)=
P(摸到白球)=
可以,只要使红球、白球的个数相等即可
2、一个袋中装有3个红球,2个白球和4个黄球,每个球除颜色外都相同,从中任意摸出一球,则:
P(摸到红球)=
P(摸到白球)=
P(摸到黄球)=
3 、一道单选题有A、B、C、D四个备选答案,当你不会做时,从中随机选一个答案,你答对的概率是多少?你答错的概率是多少?
P(答对题)=
P(答错题)=
4、掷一枚骰子,
①求点数6朝上的可能性的大小;
②求比3小的点数朝上的可能性的大小;
③求奇数点朝上的可能性的大小。
P(6点朝上)=
P(比3小的点数朝上)=
P(奇数点朝上)=
5、端午节吃粽子是中华民族的传统习俗,妈妈买了2只红豆粽子、3只牛肉粽子、5只咸肉粽子,粽子除内部馅料不同外其他均相同小颖随意吃一个,吃到红豆粽子的概率是
P(吃到红豆粽子)=
6、将A,B,C,D,E这五个字母分别写在5张同样的纸条上,并将这些纸条放在一个盒子中。搅匀后从中任意摸出一张,会出现哪些可能的结果?它们是等可能的吗?
会出现纸条A、纸条B、纸条C、纸条D、纸条E这5种结果,而且每一种结果的出现都是等可能的
7、有7张纸签,分别标有数字1,1,2,2,3,4,5,从中随机地抽出一张,求:
(1)抽出标有数字3的纸签的概率;
(2)抽出标有数字1的纸签的概率;
(3)抽出标有数字为奇数的纸签的概率。
P(抽出数字3的纸签)=
P(抽出数字1的纸签)=
P(抽出数字为奇数的纸签)=
8、一副52张的扑克牌(无大小王),从中任意取出一张,共有52种等可能的结果。
(1)求抽到红桃K的可能性的大小
(2)求抽到K的可能性的大小
P(抽到K)=
P(抽到红桃K)=
分层训练 基础题
1. 掷一个材质均匀的骰子,观察向上的一面的点数,求下列事件的概率:
(1)点数为4;(2)点数为偶数;(3)点数大于3小于6;
解:因为掷一个骰子可能发生的结果数有6种,等可能的掷出1,2,3,4,5,6这6个数
(1)∵发生点数为4的结果数只有1个,
∴P(点数为4)=
(2)∵点数为偶数的结果包括:2、4、6这3个数,
∴P(点数为偶数)=
(3)∵点数大于3小于6的结果包括:4、5这2个数,
∴P(点数大于3小于6)=
2、小敏和爸爸玩“石头剪刀布”游戏,每次用一只手出“石头”、“剪刀”、“布”三种手势之一,规则是:“石头”赢“剪刀”,“剪刀”赢“布”,“布”赢“石头”,若两人出相同手势,则算打平。
(1)你能帮小敏算算她的爸爸出“石头”手势的概率是多少?(2) 小敏赢的概率是多少?
解(1)总共有“石头”、“剪刀”、“布”这3种手势,“石头”只是其中一种,所以P(爸爸出“石头”手势)=
(2)如图所示,根据两人出的手势不同,出现的结果有9种可能,而小敏赢时,两人的手势有3种可能,所以P(小敏赢)=
小敏
小敏
小敏
爸爸
爸爸
爸爸
平
平
平
石头
石头
剪刀
剪刀
布
布
小敏
爸爸
分层训练 自助餐
1、从1、2、3、4、5、6、7、8、9、10这十个数中随机取出一个数,取出的数是3的倍数的概率是 。
2、某商场开展购物抽奖活动,抽奖箱中有200张抽奖卡,其中一等奖5张,二等奖10张,三等奖25张,其余抽奖卡无奖,则参加抽奖的某顾客从箱中随机抽取一张,他中奖的概率是 。
3、有8只型号相同的杯子,其中一等品5只,二等品2只,三等品1只,随机从中抽取一只,恰好抽到一等品的概率是 。
4、某比赛共有1-10号十个测试题供选手随机抽取作答,前两位选手分别抽走了2号、7号题,第3位选手抽走8号题的概率是 。
5、一个口袋内装有大小相等的1个白球和已编号码为1,2,3 的3个黑球,从中摸出2个球
(1)共有多少种不同结果?
(2)摸出2个黑球有多少种不同结果?
(3)摸出2个黑球的概率是多少?
白黑3
白黑2
白黑1
黑2黑3
黑1黑3
黑1黑2
解:(1)如图所示从这4个球中摸出2个的结果有白黑1,
白黑3,黑1黑2,黑1黑3,黑2黑3 6种
(2)摸到2个黑球的结果有:摸到黑1黑2,
摸到黑1黑3,摸到黑2黑3,这3种
(3)P(摸出2个黑球)=
分层训练 小测试
1.十字路口的交通信号灯每分钟红灯亮30秒,绿灯亮25秒,黄灯亮5秒,当你抬头看信号灯恰是黄灯亮的概率为______.
2.袋中有5个黑球,3个白球和2个红球,每次摸一个球,摸出后再放回,在连续摸9次且9次摸出的都是黑球的情况下,第10次摸出红球的概率为___.
3.中国象棋红方棋子按兵种小同分布如下:1个帅,5个兵,“士、象、马、车、炮”各2个,将所有棋子反面朝上放在棋盘中,任取一个不是兵和帅的概率是( )
(A) (B) (C) (D)
D
4.盆中装有大小相同的各色小球12只,其中5只红球、4只黑球、 2只白球、1只绿球,求:
①从中取出一球为红球或黑球的概率;
②从中取出一球为红球或黑球或白球的概率。
∵取出红球或黑球的结果数为5+4=9种,
∴P(取出红球或黑球)=
方法一:∵取出红球或黑球或白球的结果数为5+4+2=11
∴P(取出红球或黑球或白球)=
方法二:∵取出绿球的结果数为1
∴P(取出绿球)=
∴ P(取出红球或黑球或白球)=1-P(取出绿球)
2. 必然事件发生的概率为1,记作:P(必然件)=1;
不可能事件发生的概率为0,记作:P(不可能事件)=0
如果A为不确定事件,那么: 0<P(A) < 1
1.理解事件发生的概率的意义并能计算.
课堂小结
第1课时 与摸球相关的等可能事件的概率
教学目标
一、了解可化为古典概型的几何概型的特点,会根据试验结果的对称性或均衡性判断试验结果是否具有等可能性;
二、掌握古典概型的概率计算方法;
三、能设计符合要求的简单概率模型,初步体会概率是描述不确定现象的数学模型。
设一个实验的所有可能结果有n个,每次
试验有且只有其中的一个结果出现。如果
每个结果出现的可能性相同,那么我们就
称这个试验的结果是等可能的。这个实验
就是一个等可能事件。
袋子里装有两个球,它们除颜色外完全相同。从袋中任意摸出一球.
1.若袋中两个都是红球,摸出一个为红球,称为
事件;摸出一个为白球,称为 事件(选填“必然”“不确定”或“不可能”);
必然
不可能
2.若袋中一个为红球,一个为白球,摸出一个为红球,称为 事件.
不确定
导入新课
复习引入
必然事件发生的可能性是
100%
即1;
不可能事件发生的可能性是
0;
大于0而小于1的.
不确定事件发生的可能性是
2.三类事件发生的可能性
不可能发生
3.三类事件发生的可能性的图示法
0
1
(50%)
必然发生
可能发生
若盒子里有3个红球、1个白球,它们除颜色外完全相同,小明从盒中任摸一球.
2
3
4
1
(2)若将每个球都编上号码,分别为1号球(红)、2号球(红)、3号球(红)、4号球(白),那么摸到每个球的可能性一样吗?
(1)猜一猜,摸出的球可能是什么颜色?与同伴进行交流
讲授新课
与摸球相关的等可能事件概率
(3)任意摸出一球,你能说出所有可能出现的结果吗?
摸到红球的可能出现的结果有: 1号球、2号球、3号球.
1
2
3
4
1
(4)摸出红球可能出现的结果有哪几种?
所有可能出现的结果有:1号球、2号球、3号球、4号球
(5) 摸出红球 的可能性是多少?
人们通常用
来表示摸到红球的可能性,也叫 做摸到红球的概率
概率用字母P来表示
★ 必然事件发生的概率为
1
记作: P(必然事件)=1;
0
记作: P(不可能事件)=0;
0<P(A) < 1
★ 不可能事件发生的概率为
★ 如果A为不确定事件,那么:
三类事件发生的概率及表示
1、从分别标有1、2、3、4、5号的5个球中随机抽取一个球,抽出的号码有 种可能,
即可能摸到 ,由于这5个球的形状、大小相同,又是随机抽取的,所以我们认为:每个号码抽到的可能性 ,都是 。
2、抛一枚硬币,向上的面有 种可能,即可能抛出 ,由于硬币的构造、质地均匀,又是随机掷出的,所以我们断言:每种结果的可能性 ,都是 。
正面朝上,反面朝上
1号球,2号球,3号球,4号球,5号球
相同
相同
5
2
探索新知
①所有可能的结果是可数的
共同点:
②每种结果出现的可能性相同
A
n
m
m
n
P(A)= —
例如:一副完整的扑克牌54张,抽到A的概率?
P(抽到A)=
一般地,如果一个试验有n个等可能的结果,
事件A包含其中的m个结果,那么事件A发生的
概率为:
P(A)=
所有可能发生的结果数n
事件A发生的结果数m
(1)掷出的点数大于4的结果只有2种:
掷出的点数分别是5,6.所以
P(掷出的点数大于4)= — = —
例:任意掷一枚均匀骰子。
(1)掷出的点数大于4的概率是多少?
解析:任意掷一枚均匀骰子,所有可能的
结果有6种:掷出的点数分别是1,2,3,4,
5,6,因为骰子是均匀的,所以每种结果
出现的可能性相等。
2
6
1
3
规范作答
P(掷出的点数是偶数)= — = —
(2)掷出的点数是偶数的概率是多少?
掷出的点数是偶数的结果有3种:
掷出的点数分别是2,4,6.所以
6
3
2
1
1、一个袋中有3个红球和5个白球,每个球除颜色外都相同。从中任意摸出一球。
①摸到红球和摸到白球的概率相等吗?
②如果不等,能否通过改变袋中红球或白球的数量,使摸到的红球和白球的概率相等?
摸到红球和白球的概率不等
P(摸到红球)=
P(摸到白球)=
可以,只要使红球、白球的个数相等即可
2、一个袋中装有3个红球,2个白球和4个黄球,每个球除颜色外都相同,从中任意摸出一球,则:
P(摸到红球)=
P(摸到白球)=
P(摸到黄球)=
3 、一道单选题有A、B、C、D四个备选答案,当你不会做时,从中随机选一个答案,你答对的概率是多少?你答错的概率是多少?
P(答对题)=
P(答错题)=
4、掷一枚骰子,
①求点数6朝上的可能性的大小;
②求比3小的点数朝上的可能性的大小;
③求奇数点朝上的可能性的大小。
P(6点朝上)=
P(比3小的点数朝上)=
P(奇数点朝上)=
5、端午节吃粽子是中华民族的传统习俗,妈妈买了2只红豆粽子、3只牛肉粽子、5只咸肉粽子,粽子除内部馅料不同外其他均相同小颖随意吃一个,吃到红豆粽子的概率是
P(吃到红豆粽子)=
6、将A,B,C,D,E这五个字母分别写在5张同样的纸条上,并将这些纸条放在一个盒子中。搅匀后从中任意摸出一张,会出现哪些可能的结果?它们是等可能的吗?
会出现纸条A、纸条B、纸条C、纸条D、纸条E这5种结果,而且每一种结果的出现都是等可能的
7、有7张纸签,分别标有数字1,1,2,2,3,4,5,从中随机地抽出一张,求:
(1)抽出标有数字3的纸签的概率;
(2)抽出标有数字1的纸签的概率;
(3)抽出标有数字为奇数的纸签的概率。
P(抽出数字3的纸签)=
P(抽出数字1的纸签)=
P(抽出数字为奇数的纸签)=
8、一副52张的扑克牌(无大小王),从中任意取出一张,共有52种等可能的结果。
(1)求抽到红桃K的可能性的大小
(2)求抽到K的可能性的大小
P(抽到K)=
P(抽到红桃K)=
分层训练 基础题
1. 掷一个材质均匀的骰子,观察向上的一面的点数,求下列事件的概率:
(1)点数为4;(2)点数为偶数;(3)点数大于3小于6;
解:因为掷一个骰子可能发生的结果数有6种,等可能的掷出1,2,3,4,5,6这6个数
(1)∵发生点数为4的结果数只有1个,
∴P(点数为4)=
(2)∵点数为偶数的结果包括:2、4、6这3个数,
∴P(点数为偶数)=
(3)∵点数大于3小于6的结果包括:4、5这2个数,
∴P(点数大于3小于6)=
2、小敏和爸爸玩“石头剪刀布”游戏,每次用一只手出“石头”、“剪刀”、“布”三种手势之一,规则是:“石头”赢“剪刀”,“剪刀”赢“布”,“布”赢“石头”,若两人出相同手势,则算打平。
(1)你能帮小敏算算她的爸爸出“石头”手势的概率是多少?(2) 小敏赢的概率是多少?
解(1)总共有“石头”、“剪刀”、“布”这3种手势,“石头”只是其中一种,所以P(爸爸出“石头”手势)=
(2)如图所示,根据两人出的手势不同,出现的结果有9种可能,而小敏赢时,两人的手势有3种可能,所以P(小敏赢)=
小敏
小敏
小敏
爸爸
爸爸
爸爸
平
平
平
石头
石头
剪刀
剪刀
布
布
小敏
爸爸
分层训练 自助餐
1、从1、2、3、4、5、6、7、8、9、10这十个数中随机取出一个数,取出的数是3的倍数的概率是 。
2、某商场开展购物抽奖活动,抽奖箱中有200张抽奖卡,其中一等奖5张,二等奖10张,三等奖25张,其余抽奖卡无奖,则参加抽奖的某顾客从箱中随机抽取一张,他中奖的概率是 。
3、有8只型号相同的杯子,其中一等品5只,二等品2只,三等品1只,随机从中抽取一只,恰好抽到一等品的概率是 。
4、某比赛共有1-10号十个测试题供选手随机抽取作答,前两位选手分别抽走了2号、7号题,第3位选手抽走8号题的概率是 。
5、一个口袋内装有大小相等的1个白球和已编号码为1,2,3 的3个黑球,从中摸出2个球
(1)共有多少种不同结果?
(2)摸出2个黑球有多少种不同结果?
(3)摸出2个黑球的概率是多少?
白黑3
白黑2
白黑1
黑2黑3
黑1黑3
黑1黑2
解:(1)如图所示从这4个球中摸出2个的结果有白黑1,
白黑3,黑1黑2,黑1黑3,黑2黑3 6种
(2)摸到2个黑球的结果有:摸到黑1黑2,
摸到黑1黑3,摸到黑2黑3,这3种
(3)P(摸出2个黑球)=
分层训练 小测试
1.十字路口的交通信号灯每分钟红灯亮30秒,绿灯亮25秒,黄灯亮5秒,当你抬头看信号灯恰是黄灯亮的概率为______.
2.袋中有5个黑球,3个白球和2个红球,每次摸一个球,摸出后再放回,在连续摸9次且9次摸出的都是黑球的情况下,第10次摸出红球的概率为___.
3.中国象棋红方棋子按兵种小同分布如下:1个帅,5个兵,“士、象、马、车、炮”各2个,将所有棋子反面朝上放在棋盘中,任取一个不是兵和帅的概率是( )
(A) (B) (C) (D)
D
4.盆中装有大小相同的各色小球12只,其中5只红球、4只黑球、 2只白球、1只绿球,求:
①从中取出一球为红球或黑球的概率;
②从中取出一球为红球或黑球或白球的概率。
∵取出红球或黑球的结果数为5+4=9种,
∴P(取出红球或黑球)=
方法一:∵取出红球或黑球或白球的结果数为5+4+2=11
∴P(取出红球或黑球或白球)=
方法二:∵取出绿球的结果数为1
∴P(取出绿球)=
∴ P(取出红球或黑球或白球)=1-P(取出绿球)
2. 必然事件发生的概率为1,记作:P(必然件)=1;
不可能事件发生的概率为0,记作:P(不可能事件)=0
如果A为不确定事件,那么: 0<P(A) < 1
1.理解事件发生的概率的意义并能计算.
课堂小结
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
