北师大版七年级下册数学1.2 幂的乘方与积的乘方课件 (第2课时 共22张PPT)
文档属性
| 名称 | 北师大版七年级下册数学1.2 幂的乘方与积的乘方课件 (第2课时 共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 301.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-18 15:53:02 | ||
图片预览







文档简介
1.2 幂的乘方与积的乘方(第2课时)
第一章 整式的乘除
学习目标:
1、掌握积的乘方法则,并能熟练应用该法则进行计算。
2、在探索积的乘方法则的过程中,培养和发展学习数学的主动性。
重点:掌握积的乘方法则。
难点:积的乘方法则的应用。
复习回顾
2.同底数幂的乘法运算法则:
1.幂的意义:
a·a· … ·a
n个a
an
=
am · an =am+n(m, n都是正整数)
3.幂的乘方运算法则:
(am)n=amn (m, n都是正整数)
地球可以近似地看做是球体,地球的半径约为6×103 km,它的体积大约是多少立方千米?
V= —πr3 = —π×(6×103)3
3
4
3
4
那么, (6×103)3 =?
这种运算有什么特征?
探索交流
导入新课
1.计算:
(1) 10×102× 103 =______ ;(2) (x5 )2=_________.
x10
106
2.(1)同底数幂的乘法 :am·an= ( m,n都是正整数).
am+n
(2)幂的乘方:(am)n= (m,n都是正整数).
amn
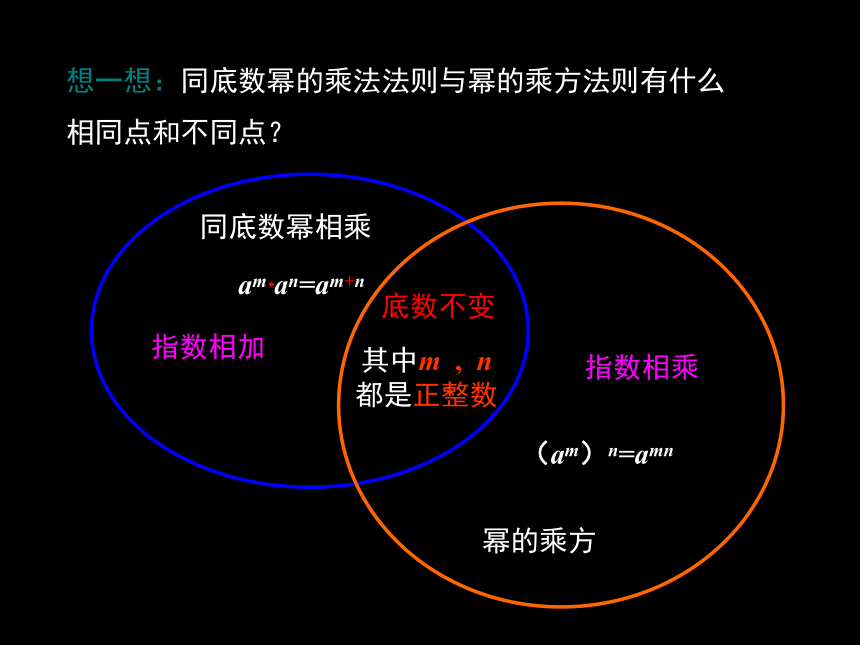
底数不变
指数相乘
指数相加
同底数幂相乘
幂的乘方
其中m , n都是正整数
(am)n=amn
am·an=am+n
想一想:同底数幂的乘法法则与幂的乘方法则有什么相同点和不同点?
讲授新课
积的乘方
一
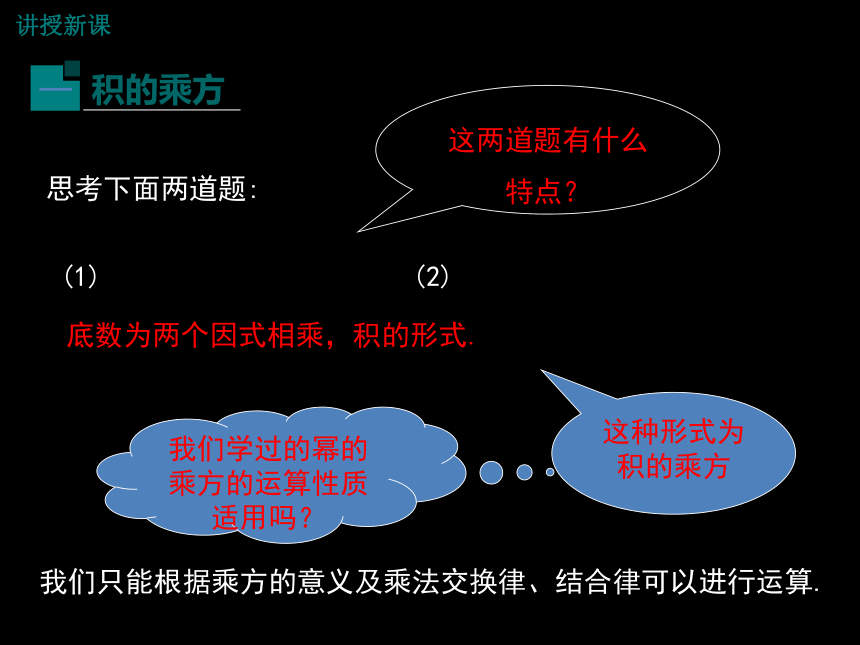
思考下面两道题:
(1)
(2)
我们只能根据乘方的意义及乘法交换律、结合律可以进行运算.
这两道题有什么特点?
底数为两个因式相乘,积的形式.
这种形式为积的乘方
我们学过的幂的乘方的运算性质适用吗?
同理:
(乘方的意义)
(乘法交换律、结合律)
(同底数幂相乘的法则)
(ab) n= (ab)· (ab)· ··· ·(ab)
n个ab
=(a·a· ··· ·a)·(b·b· ··· ·b)
n个a
n个b
=anbn.
证明:
思考问题:积的乘方(ab)n =?
猜想结论:
因此可得:(ab)n=anbn (n为正整数).
(ab)n=anbn (n为正整数)
推理验证
积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘.
(ab)n = anbn (n为正整数)
想一想:三个或三个以上的积的乘方等于什么?
(abc)n = anbncn (n为正整数)
知识要点
积的乘方法则
(1) 根据幂的意义,(ab)3表示什么?
=a·a·a · b·b·b
=a3·b3
(2)由 (ab)3=a3b3 出发, 你能想到更为一般的公式吗?
猜想
(ab)n=
anbn
(ab)3=
ab·ab·ab
不妨先思考(ab)3=?
探索交流
探索交流
(ab)n = ab·ab·……·ab ( )
=(a·a·……·a) (b·b·……·b) ( )
=an·bn. ( )
幂的意义
乘法交换律、结合律
幂的意义
n个ab
n个a
n个b
探索交流
(ab)n =
an·bn
积的乘方
乘方的积
(m,n都是正整数)
积的乘方法则
积的乘方,等于 每一因数乘方的积 .
知识扩充
三个或三个以上的积的乘方,是否也具有上面的性质? 怎样用公式表示?
(abc)n=an·bn·cn
巩固新知
例2 计算:
(1) (3x)2 ; (2) (-2b)5 ;
(3) (-2xy)4 ; (4) (3a2)n .
巩固新知
引例:地球可以近似地看做是球体,地球的半径约为6×103 km,它的体积大约是多少立方千米?
1.下面的计算是否正确?如有错误请改正:
(1) (ab4)4 = ab8 ; (2) (-3pq)2 = –6p2q2
2. 计算:
(1) (- 3n)3 ; (2) (5xy)3 ;
(3) –a3 +(–4a)2 a (4) (-3x3)2-[(2x)2]3
巩固新知
随堂练习:
(ab)n = an·bn (m, n都是正整数)
反向使用:
an·bn = (ab)n
计算:
(1)23×53 (2) 28×58
(3) (-5)16× (-2)15 (4) 24×44×(-0.125)4
(5) 0.25100×4100 (6) 812×0.12513
公式逆用
当堂练习
(1)(ab2)3=ab6 ( )
×
×
×
(2) (3xy)3=9x3y3 ( )
×
(3) (-2a2)2=-4a4 ( )
(4) -(-ab2)2=a2b4 ( )
1.判断:
2.下列运算正确的是( )
A. x.x2=x2 B. (xy)2=xy2 C.(x2)3=x6 D.x2+x2=x4
C
3. (0.04)2013×[(-5)2013]2=________.
你有几种解法?
1
(1) (ab)8 ; (2) (2m)3 ; (3) (-xy)5;
(4) (5ab2)3 ; (5) (2×102)2 ; (6) (-3×103)3.
4.计算:
解:(1)原式=a8·b8;
(2)原式= 23 ·m3=8m3;
(3)原式=(-x)5 ·y5=-x5y5;
(4)原式=53 ·a3 ·(b2)3=125 a3 b6;
(5)原式=22 ×(102)2=4 ×104;
(6)原式=(-3)3 ×(103)3=-27 ×109=-2.7 ×1010.
(1) 2(x3)2·x3-(3x3)3+(5x)2·x7;
(2)(3xy2)2+(-4xy3) · (-xy) ;
(3)(-2x3)3·(x2)2.
解:原式=2x6·x3-27x9+25x2·x7
= 2x9-27x9+25x9 = 0;
解:原式=9x2y4 +4x2y4
=13x2y4;
解:原式= -8x9·x4 =-8x13.
注意:运算顺序是
先乘方,再乘除,
最后算加减.
5.计算:
课堂小结
幂的运算性质
性质
am·an=am+n (am)n=amn
(ab)n=anbn ( m、n都是正整数)
反向运用
am · an =am+n、
(am)n =amn
an·bn = (ab)n
可使某些计算简捷
注意
运用积的乘方法则时要注意:
公式中的a、b代表任何代数式;每一个因式都要“乘方”;注意结果的符号、幂指数及其逆向运用(混合运算要注意运算顺序)
第一章 整式的乘除
学习目标:
1、掌握积的乘方法则,并能熟练应用该法则进行计算。
2、在探索积的乘方法则的过程中,培养和发展学习数学的主动性。
重点:掌握积的乘方法则。
难点:积的乘方法则的应用。
复习回顾
2.同底数幂的乘法运算法则:
1.幂的意义:
a·a· … ·a
n个a
an
=
am · an =am+n(m, n都是正整数)
3.幂的乘方运算法则:
(am)n=amn (m, n都是正整数)
地球可以近似地看做是球体,地球的半径约为6×103 km,它的体积大约是多少立方千米?
V= —πr3 = —π×(6×103)3
3
4
3
4
那么, (6×103)3 =?
这种运算有什么特征?
探索交流
导入新课
1.计算:
(1) 10×102× 103 =______ ;(2) (x5 )2=_________.
x10
106
2.(1)同底数幂的乘法 :am·an= ( m,n都是正整数).
am+n
(2)幂的乘方:(am)n= (m,n都是正整数).
amn
底数不变
指数相乘
指数相加
同底数幂相乘
幂的乘方
其中m , n都是正整数
(am)n=amn
am·an=am+n
想一想:同底数幂的乘法法则与幂的乘方法则有什么相同点和不同点?
讲授新课
积的乘方
一
思考下面两道题:
(1)
(2)
我们只能根据乘方的意义及乘法交换律、结合律可以进行运算.
这两道题有什么特点?
底数为两个因式相乘,积的形式.
这种形式为积的乘方
我们学过的幂的乘方的运算性质适用吗?
同理:
(乘方的意义)
(乘法交换律、结合律)
(同底数幂相乘的法则)
(ab) n= (ab)· (ab)· ··· ·(ab)
n个ab
=(a·a· ··· ·a)·(b·b· ··· ·b)
n个a
n个b
=anbn.
证明:
思考问题:积的乘方(ab)n =?
猜想结论:
因此可得:(ab)n=anbn (n为正整数).
(ab)n=anbn (n为正整数)
推理验证
积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘.
(ab)n = anbn (n为正整数)
想一想:三个或三个以上的积的乘方等于什么?
(abc)n = anbncn (n为正整数)
知识要点
积的乘方法则
(1) 根据幂的意义,(ab)3表示什么?
=a·a·a · b·b·b
=a3·b3
(2)由 (ab)3=a3b3 出发, 你能想到更为一般的公式吗?
猜想
(ab)n=
anbn
(ab)3=
ab·ab·ab
不妨先思考(ab)3=?
探索交流
探索交流
(ab)n = ab·ab·……·ab ( )
=(a·a·……·a) (b·b·……·b) ( )
=an·bn. ( )
幂的意义
乘法交换律、结合律
幂的意义
n个ab
n个a
n个b
探索交流
(ab)n =
an·bn
积的乘方
乘方的积
(m,n都是正整数)
积的乘方法则
积的乘方,等于 每一因数乘方的积 .
知识扩充
三个或三个以上的积的乘方,是否也具有上面的性质? 怎样用公式表示?
(abc)n=an·bn·cn
巩固新知
例2 计算:
(1) (3x)2 ; (2) (-2b)5 ;
(3) (-2xy)4 ; (4) (3a2)n .
巩固新知
引例:地球可以近似地看做是球体,地球的半径约为6×103 km,它的体积大约是多少立方千米?
1.下面的计算是否正确?如有错误请改正:
(1) (ab4)4 = ab8 ; (2) (-3pq)2 = –6p2q2
2. 计算:
(1) (- 3n)3 ; (2) (5xy)3 ;
(3) –a3 +(–4a)2 a (4) (-3x3)2-[(2x)2]3
巩固新知
随堂练习:
(ab)n = an·bn (m, n都是正整数)
反向使用:
an·bn = (ab)n
计算:
(1)23×53 (2) 28×58
(3) (-5)16× (-2)15 (4) 24×44×(-0.125)4
(5) 0.25100×4100 (6) 812×0.12513
公式逆用
当堂练习
(1)(ab2)3=ab6 ( )
×
×
×
(2) (3xy)3=9x3y3 ( )
×
(3) (-2a2)2=-4a4 ( )
(4) -(-ab2)2=a2b4 ( )
1.判断:
2.下列运算正确的是( )
A. x.x2=x2 B. (xy)2=xy2 C.(x2)3=x6 D.x2+x2=x4
C
3. (0.04)2013×[(-5)2013]2=________.
你有几种解法?
1
(1) (ab)8 ; (2) (2m)3 ; (3) (-xy)5;
(4) (5ab2)3 ; (5) (2×102)2 ; (6) (-3×103)3.
4.计算:
解:(1)原式=a8·b8;
(2)原式= 23 ·m3=8m3;
(3)原式=(-x)5 ·y5=-x5y5;
(4)原式=53 ·a3 ·(b2)3=125 a3 b6;
(5)原式=22 ×(102)2=4 ×104;
(6)原式=(-3)3 ×(103)3=-27 ×109=-2.7 ×1010.
(1) 2(x3)2·x3-(3x3)3+(5x)2·x7;
(2)(3xy2)2+(-4xy3) · (-xy) ;
(3)(-2x3)3·(x2)2.
解:原式=2x6·x3-27x9+25x2·x7
= 2x9-27x9+25x9 = 0;
解:原式=9x2y4 +4x2y4
=13x2y4;
解:原式= -8x9·x4 =-8x13.
注意:运算顺序是
先乘方,再乘除,
最后算加减.
5.计算:
课堂小结
幂的运算性质
性质
am·an=am+n (am)n=amn
(ab)n=anbn ( m、n都是正整数)
反向运用
am · an =am+n、
(am)n =amn
an·bn = (ab)n
可使某些计算简捷
注意
运用积的乘方法则时要注意:
公式中的a、b代表任何代数式;每一个因式都要“乘方”;注意结果的符号、幂指数及其逆向运用(混合运算要注意运算顺序)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
