4.1认识三角形(1)-北师大版七年级下册数学课件 (共43张PPT)
文档属性
| 名称 | 4.1认识三角形(1)-北师大版七年级下册数学课件 (共43张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 636.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-18 08:57:28 | ||
图片预览







文档简介
第四章 三角形
4.1.1 认识三角形
1.了解三角形及相关概念,能正确识别和表示三角形;
2. 会按角的大小对三角形进行分类;
3.掌握三角形的内角等于180°,并会据此解决简单的问
题.(重点、难点)
学习目标
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
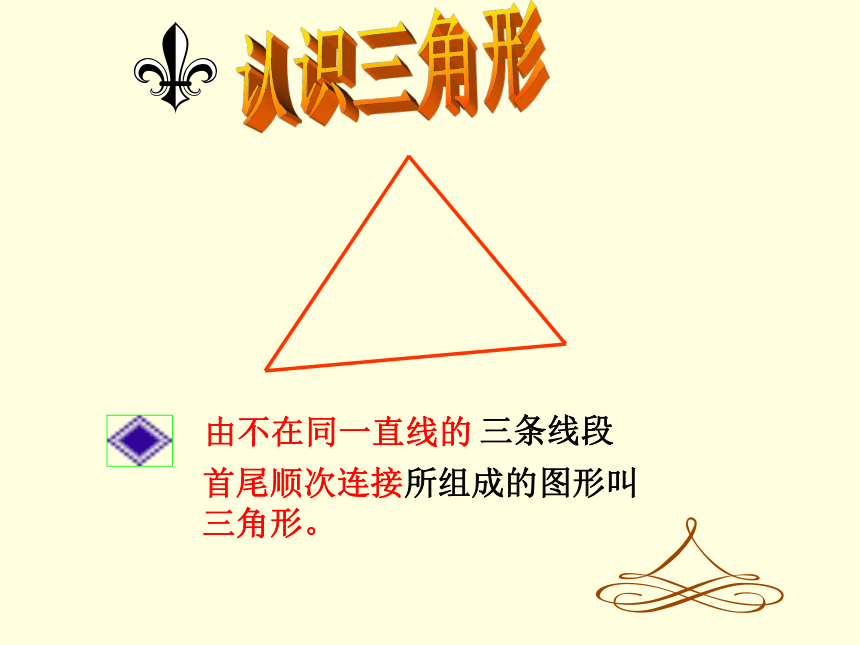
认识三角形
三条线段
由不在同一直线的
首尾顺次连接所组成的图形叫三角形。
三个顶点
三个内角
A
B
C
三条边
C
B
A
“三角形”可以用符号“Δ”表示
ΔABC
C
B
A
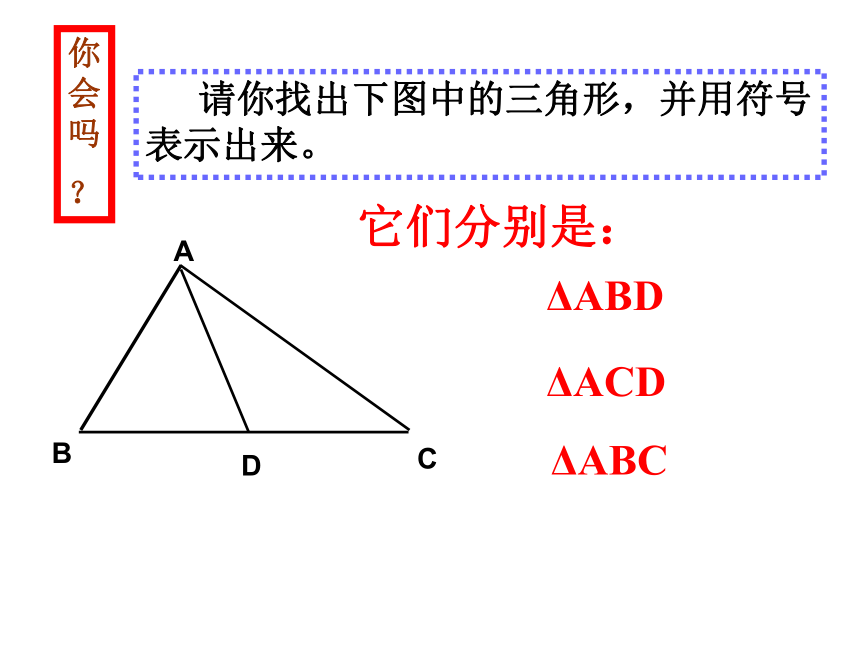
D
ΔABD
ΔACD
ΔABC
你会吗
?
请你找出下图中的三角形,并用符号表示出来。
它们分别是:
可用顶点的两个大写字母表示。
A
B
C
c
b
a
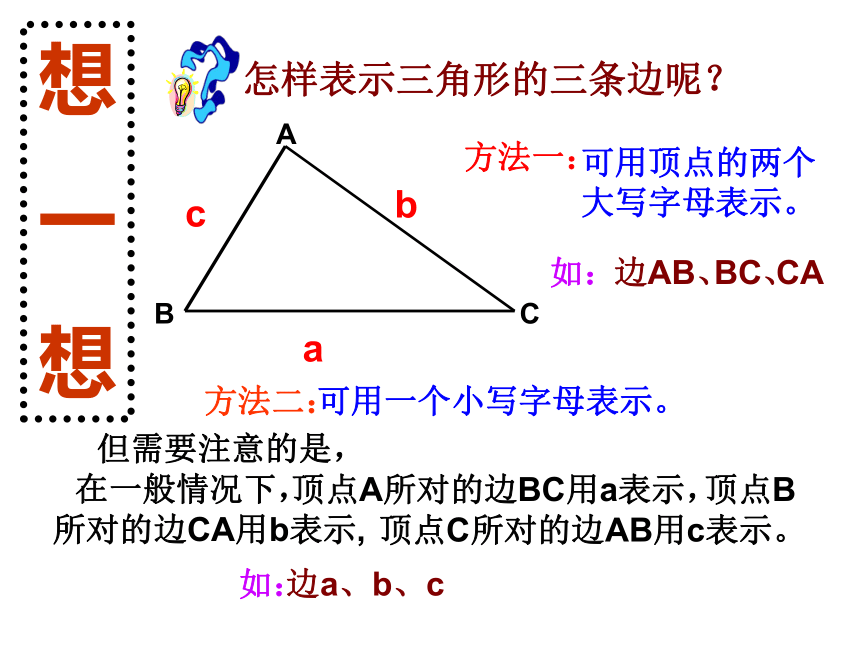
想
一
想
怎样表示三角形的三条边呢?
方法一:
如:
边AB、
BC、
CA
方法二:
可用一个小写字母表示。
但需要注意的是,
在一般情况下,
如:
边a、b、c
顶点B所对的边CA用b表示,
顶点C所对的边AB用c表示。
顶点A所对的边BC用a表示,
?
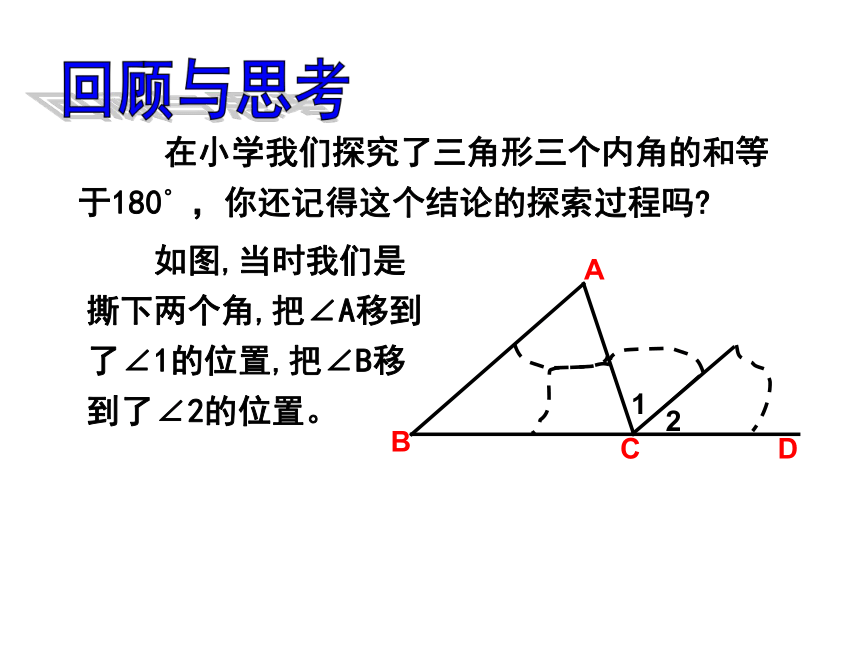
在小学我们探究了三角形三个内角的和等于180? ,你还记得这个结论的探索过程吗?
1
A
B
D
2
C
如图,当时我们是撕下两个角,把∠A移到了∠1的位置,把∠B移到了∠2的位置。
回顾与思考
拼一拼,说一说
如果只撕下一个角,你能用学过的知识拼凑并解释“三角形的三个内角和是180?”吗?
1
2
3
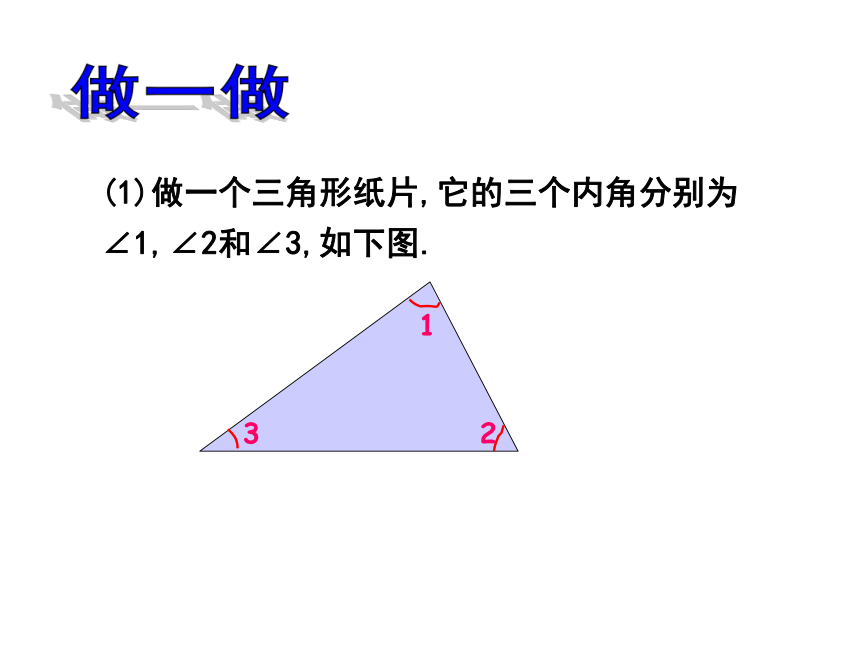
(1)做一个三角形纸片,它的三个内角分别为∠1,∠2和∠3,如下图.
做一做
1
2
3
(2)将∠1撕下,并按上图进行摆放,其中∠1的顶点与∠2的顶点重合,它的一条边与∠2的一条边重合.此时∠1的另一条边b与∠3的一条边a 平行吗?为什么?
1
a
b
做一做
1
2
3
1
a
b
(3)将∠2与∠3的公共边延长,它与b所夹的角为∠4. ∠3与∠4的大小有什么关系?为什么?
4
做一做
想一想
由此你能得到什么结论?
三角形的三个内角和等于180度.
想一想
你会用几何语言进行证明吗?
证明:
在△ABC的外部,
以CA为一边,
CE为另一边作∠1=∠A,
作BC的延长线CD,
于是CE∥BA
(内错角相等,两直线平行).
∴∠B=∠2
(两直线平行,同位角相等).
又∵∠1+∠2+∠ACB=180°
(平角的定义)
∴∠A+∠B+∠ACB=180°
(等量代换)
)
1
2
C
A
E
)
B
D
想一想
还有其他证明方法吗?
证法2:
)
1
2
C
A
E
)
B
D
过C作CE∥BA.
作BC的延长线CD,
于是∠A=∠1
(两直线平行,内错角相等)
∠B=∠2
又∵∠1+∠2+∠ACB=180°
(平角的定义)
∴∠A+∠B+∠ACB=180°
(两直线平行,同位角相等)
(等量代换)
C
A
B
E
F
证法3:
过A作EF∥BC
试一试
C
A
B
E
证法4:
过A作AE∥BC
试一试
下面的图⑴、图⑵、图⑶中的三角形被遮住的两个内角是什么角?试着说明理由。
猜一猜
将图⑶的结果与图⑴、图⑵的结果进行比较,可以将三角形如何按角分类?
猜一猜
三角形的分类
锐角三角形
三个内角都是锐角
钝角三角形
有一个内角是钝角
直角三角形
有一个内角是直角
按三角形内角的大小把三角形分为三类
直角边
直角边
斜边
1.常用符号“Rt?ABC”来表示
直角三角形ABC.
2.直角三角形的两个锐角之间
有什么关系?
直角三角形
直角三角形的两个锐角互余
1.观察下面的三角形,并把它们的标号填入相应图内:
锐角三角形 直角三角形 钝角三角形
③⑤
①④⑥
②⑦
练一练
1.一个三角形两个内角的度数分别如下,这个三角形是什么三角形?
(1)30度和60度
(2)40度和70度
(3)50度和20度
练一练
直角三角形
锐角三角形
钝角三角形
练一练
2.在下面的空白处,分别填入“锐角”,“钝角”
或“直角”:
(1)如果三角形的三个内角都相等,那么这个三角形是 三角形;
(2)如果三角形的一个内角等于另外两个 内角之和,那么这个三角形是 三角形;
(3)如果三角形的两个内角都小于40度,那么这个三角形是 三角形.
钝角
锐角
直角
练一练
3. △ABC中, ∠A:∠B:∠C=2:3:4,则
∠A= , ∠B= , ∠C= .
4.在△ABC中, ∠A=1/3∠B=1/5∠C,则△ABC
是 三角形.
40°
80°
60°
钝角
5.已知∠ACB=90°,CD⊥AB,垂足为D.
⑴ 图中有几个直角三角形?是哪几个?分别说出它们的直角边和斜边。
⑵ ∠ACD和∠A有什么关系?∠BCD和∠A呢?
C
B
A
D
练一练
C
B
A
D
练一练
解:直角三角形有三个,分别是:
Rt?BDC
Rt?ADC
Rt?ACB
直角边是AC、BC,斜边AB
直角边是AD、CD,斜边AC
直角边是BD、CD,斜边BC
C
B
A
D
练一练
解: ∠ACD和∠A互余
∠BCD和∠A相等
又∵ ∠ACD+∠A + ∠ADC =180°
证明:在Rt?ADC中,∵ CD⊥AB , ∴∠ADC =90°
∴ ∠ACD+∠A =90°
又∵ ∠ACD+ ∠BCD= 90°
∴ ∠BCD=∠A
一个三角形中会有两个直角?可能两个内角是钝角或锐角吗?
想一想
1. 已知∠A,∠B,∠C是△ABC的三个内角,∠A=70°,∠C=30 °, ∠B=( ).
2. 直角三角形一个锐角为70°,另一个锐角等于( ).
80 °
20 °
练一练
3.在△ABC中,∠A=80°,∠B=∠C,则∠C=( ).
4.如果△ABC中,∠A∶∠B∶∠C=2∶3∶5,此三角形按 角分类应为 ( ).
50 °
直角三角形
练一练
有关三角形的角度计算问题,有两种类型:一是直接利用三角形的内角和180°进行计算;二是设某一个角为x(或将某一个角视为未知数),其余的角用x的代数式表示,从而根据题意列出方程(组)求解,这就是“形题数解”。
方法规律
实际问题
如图,一艘轮船按箭头所示方向行驶,C处有一灯塔,请你根据图中所标数据求∠ACB的大小,当轮船距离灯塔C最近时,∠ACB是多少度?
30 °
70 °
B
C
A
E
实际问题
30 °
70 °
B
C
A
E
解:∵∠ABC+∠CBE= 180°
∴ ∠ABC= 180°-∠CBE= 180°- 70°= 110°
∴在?ABC中, ∠ACB= 180°- ∠ABC - ∠A
= 180°- 110° - 30°
= 40°
实际问题
30 °
90 °
B
C
A
解:当轮船距离灯塔C最近时,则有CB⊥AB
即∠ACB = 90°
∴在?ABC中, ∠ACB= 180°- ∠ABC - ∠A
= 180°- 90° - 30°
= 60°
课堂小结
1.三角形三个内角的和等于180 ? .
2.三角形按角的大小分类:
⑴锐角三角形 :三个内角都是锐角;
⑵直角三角形 :有一个内角为直角;
⑶钝角三角形 :有一个内角为钝角 。
3.直角三角形的两个锐角互余。
请你谈一谈:
通过这节课的学习,你对三角形又多了哪些认识?
三角形
三角形的概念:由不在同一条直线上的三条线段首尾依次相接所组成的封闭图形.
课堂小结
三角形按角分类
直角三角形
锐角三角形
钝角三角形
三角形的内角和等于180°
作业
以三角形为主设计一幅美丽图案并说说你的设计意图,作品我们将公开展览。
2、请你做个“小小设计师”
4.1.1 认识三角形
1.了解三角形及相关概念,能正确识别和表示三角形;
2. 会按角的大小对三角形进行分类;
3.掌握三角形的内角等于180°,并会据此解决简单的问
题.(重点、难点)
学习目标
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
认识三角形
三条线段
由不在同一直线的
首尾顺次连接所组成的图形叫三角形。
三个顶点
三个内角
A
B
C
三条边
C
B
A
“三角形”可以用符号“Δ”表示
ΔABC
C
B
A
D
ΔABD
ΔACD
ΔABC
你会吗
?
请你找出下图中的三角形,并用符号表示出来。
它们分别是:
可用顶点的两个大写字母表示。
A
B
C
c
b
a
想
一
想
怎样表示三角形的三条边呢?
方法一:
如:
边AB、
BC、
CA
方法二:
可用一个小写字母表示。
但需要注意的是,
在一般情况下,
如:
边a、b、c
顶点B所对的边CA用b表示,
顶点C所对的边AB用c表示。
顶点A所对的边BC用a表示,
?
在小学我们探究了三角形三个内角的和等于180? ,你还记得这个结论的探索过程吗?
1
A
B
D
2
C
如图,当时我们是撕下两个角,把∠A移到了∠1的位置,把∠B移到了∠2的位置。
回顾与思考
拼一拼,说一说
如果只撕下一个角,你能用学过的知识拼凑并解释“三角形的三个内角和是180?”吗?
1
2
3
(1)做一个三角形纸片,它的三个内角分别为∠1,∠2和∠3,如下图.
做一做
1
2
3
(2)将∠1撕下,并按上图进行摆放,其中∠1的顶点与∠2的顶点重合,它的一条边与∠2的一条边重合.此时∠1的另一条边b与∠3的一条边a 平行吗?为什么?
1
a
b
做一做
1
2
3
1
a
b
(3)将∠2与∠3的公共边延长,它与b所夹的角为∠4. ∠3与∠4的大小有什么关系?为什么?
4
做一做
想一想
由此你能得到什么结论?
三角形的三个内角和等于180度.
想一想
你会用几何语言进行证明吗?
证明:
在△ABC的外部,
以CA为一边,
CE为另一边作∠1=∠A,
作BC的延长线CD,
于是CE∥BA
(内错角相等,两直线平行).
∴∠B=∠2
(两直线平行,同位角相等).
又∵∠1+∠2+∠ACB=180°
(平角的定义)
∴∠A+∠B+∠ACB=180°
(等量代换)
)
1
2
C
A
E
)
B
D
想一想
还有其他证明方法吗?
证法2:
)
1
2
C
A
E
)
B
D
过C作CE∥BA.
作BC的延长线CD,
于是∠A=∠1
(两直线平行,内错角相等)
∠B=∠2
又∵∠1+∠2+∠ACB=180°
(平角的定义)
∴∠A+∠B+∠ACB=180°
(两直线平行,同位角相等)
(等量代换)
C
A
B
E
F
证法3:
过A作EF∥BC
试一试
C
A
B
E
证法4:
过A作AE∥BC
试一试
下面的图⑴、图⑵、图⑶中的三角形被遮住的两个内角是什么角?试着说明理由。
猜一猜
将图⑶的结果与图⑴、图⑵的结果进行比较,可以将三角形如何按角分类?
猜一猜
三角形的分类
锐角三角形
三个内角都是锐角
钝角三角形
有一个内角是钝角
直角三角形
有一个内角是直角
按三角形内角的大小把三角形分为三类
直角边
直角边
斜边
1.常用符号“Rt?ABC”来表示
直角三角形ABC.
2.直角三角形的两个锐角之间
有什么关系?
直角三角形
直角三角形的两个锐角互余
1.观察下面的三角形,并把它们的标号填入相应图内:
锐角三角形 直角三角形 钝角三角形
③⑤
①④⑥
②⑦
练一练
1.一个三角形两个内角的度数分别如下,这个三角形是什么三角形?
(1)30度和60度
(2)40度和70度
(3)50度和20度
练一练
直角三角形
锐角三角形
钝角三角形
练一练
2.在下面的空白处,分别填入“锐角”,“钝角”
或“直角”:
(1)如果三角形的三个内角都相等,那么这个三角形是 三角形;
(2)如果三角形的一个内角等于另外两个 内角之和,那么这个三角形是 三角形;
(3)如果三角形的两个内角都小于40度,那么这个三角形是 三角形.
钝角
锐角
直角
练一练
3. △ABC中, ∠A:∠B:∠C=2:3:4,则
∠A= , ∠B= , ∠C= .
4.在△ABC中, ∠A=1/3∠B=1/5∠C,则△ABC
是 三角形.
40°
80°
60°
钝角
5.已知∠ACB=90°,CD⊥AB,垂足为D.
⑴ 图中有几个直角三角形?是哪几个?分别说出它们的直角边和斜边。
⑵ ∠ACD和∠A有什么关系?∠BCD和∠A呢?
C
B
A
D
练一练
C
B
A
D
练一练
解:直角三角形有三个,分别是:
Rt?BDC
Rt?ADC
Rt?ACB
直角边是AC、BC,斜边AB
直角边是AD、CD,斜边AC
直角边是BD、CD,斜边BC
C
B
A
D
练一练
解: ∠ACD和∠A互余
∠BCD和∠A相等
又∵ ∠ACD+∠A + ∠ADC =180°
证明:在Rt?ADC中,∵ CD⊥AB , ∴∠ADC =90°
∴ ∠ACD+∠A =90°
又∵ ∠ACD+ ∠BCD= 90°
∴ ∠BCD=∠A
一个三角形中会有两个直角?可能两个内角是钝角或锐角吗?
想一想
1. 已知∠A,∠B,∠C是△ABC的三个内角,∠A=70°,∠C=30 °, ∠B=( ).
2. 直角三角形一个锐角为70°,另一个锐角等于( ).
80 °
20 °
练一练
3.在△ABC中,∠A=80°,∠B=∠C,则∠C=( ).
4.如果△ABC中,∠A∶∠B∶∠C=2∶3∶5,此三角形按 角分类应为 ( ).
50 °
直角三角形
练一练
有关三角形的角度计算问题,有两种类型:一是直接利用三角形的内角和180°进行计算;二是设某一个角为x(或将某一个角视为未知数),其余的角用x的代数式表示,从而根据题意列出方程(组)求解,这就是“形题数解”。
方法规律
实际问题
如图,一艘轮船按箭头所示方向行驶,C处有一灯塔,请你根据图中所标数据求∠ACB的大小,当轮船距离灯塔C最近时,∠ACB是多少度?
30 °
70 °
B
C
A
E
实际问题
30 °
70 °
B
C
A
E
解:∵∠ABC+∠CBE= 180°
∴ ∠ABC= 180°-∠CBE= 180°- 70°= 110°
∴在?ABC中, ∠ACB= 180°- ∠ABC - ∠A
= 180°- 110° - 30°
= 40°
实际问题
30 °
90 °
B
C
A
解:当轮船距离灯塔C最近时,则有CB⊥AB
即∠ACB = 90°
∴在?ABC中, ∠ACB= 180°- ∠ABC - ∠A
= 180°- 90° - 30°
= 60°
课堂小结
1.三角形三个内角的和等于180 ? .
2.三角形按角的大小分类:
⑴锐角三角形 :三个内角都是锐角;
⑵直角三角形 :有一个内角为直角;
⑶钝角三角形 :有一个内角为钝角 。
3.直角三角形的两个锐角互余。
请你谈一谈:
通过这节课的学习,你对三角形又多了哪些认识?
三角形
三角形的概念:由不在同一条直线上的三条线段首尾依次相接所组成的封闭图形.
课堂小结
三角形按角分类
直角三角形
锐角三角形
钝角三角形
三角形的内角和等于180°
作业
以三角形为主设计一幅美丽图案并说说你的设计意图,作品我们将公开展览。
2、请你做个“小小设计师”
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
